Publicamos la solución al divertimento Cañas de Bambú. Gracias a Javier Ribelles y Carmen Zuleta, Marcos Jimémez y Manuel Zambrana, y Don Diedro y D. Pablo por las soluciones que nos han hecho llegar. Se han recibido soluciones parciales.
Divertimento:
Una terraza de un chiringuito en la playa está delimitada por una valla en forma de circunferencia con centro en el punto \(O=(0,0)\) y radio igual a 50 metros. Se plantan cañas de bambú idénticas en todos los puntos de coordenadas enteras salvo en \(O\). La valla será visible para un observador ubicado en el punto \(O\) si el radio \(r\) de las cañas de bambú no es demasiado grande:

(en la imagen no aparecen todas las cañas). Se pide demostrar que la valla no es visible desde \(O\) si \(r>1/50\) metros, pero sí es visible si \(r<1/\sqrt{2501}\) metros.
Solución:
En esta ocasión publicamos dos soluciones distintas. La primera es la propuesta por los coordinadores de la sección, que consideramos que es interesante por las ideas que se utilizan. La segunda está propuesta por Marcos Jiménez y Manuel Zambrana, que han determinado el valor exacto de \(r\) a partir del que se dejan de ver las vallas.
Solución propuesta por los coordinadores de la sección:
Comenzamos probando que, si \(r<1/\sqrt{2501}\) y \(R=(50,1)\), el segmento \(OR\) no corta a ninguna caña de bambú. Se tiene que \(OR=\sqrt{2501}\). Si \(S\) es otro punto cualquiera del retículo, entonces el área del triángulo \(ORS\) es al menos \(1/2\) (pues esa es el menor área posible para un triángulo con tres vértices en un retículo). Sea \(T\) la proyección ortogonal de \(S\) sobre \(OR\).

El área del triángulo \(ORS\) es \(A=\frac{1}{2} OR \cdot ST\). Por tanto, $$\frac{1}{2} OR \cdot ST \geq \frac{1}{2},$$ de donde $$ST \geq \frac{1}{OR} = \frac{1}{\sqrt{2501}} >r,$$ es decir, la caña de bambú de centro \(S\) y radio \(r\) no corta al segmento \(OR\), y la valla es visible desde \(O\).
Veamos ahora que si \(r>1/50\) entonces las cañas no dejan ver la valla en ninguna dirección. Consideremos un diámetro \(MN\) y el rectángulo \(ABCD\) en el que los segmentos \(AC\) y \(BD\) son paralelos a \(MN\) y \(AN=NB=CM=MD=r\).
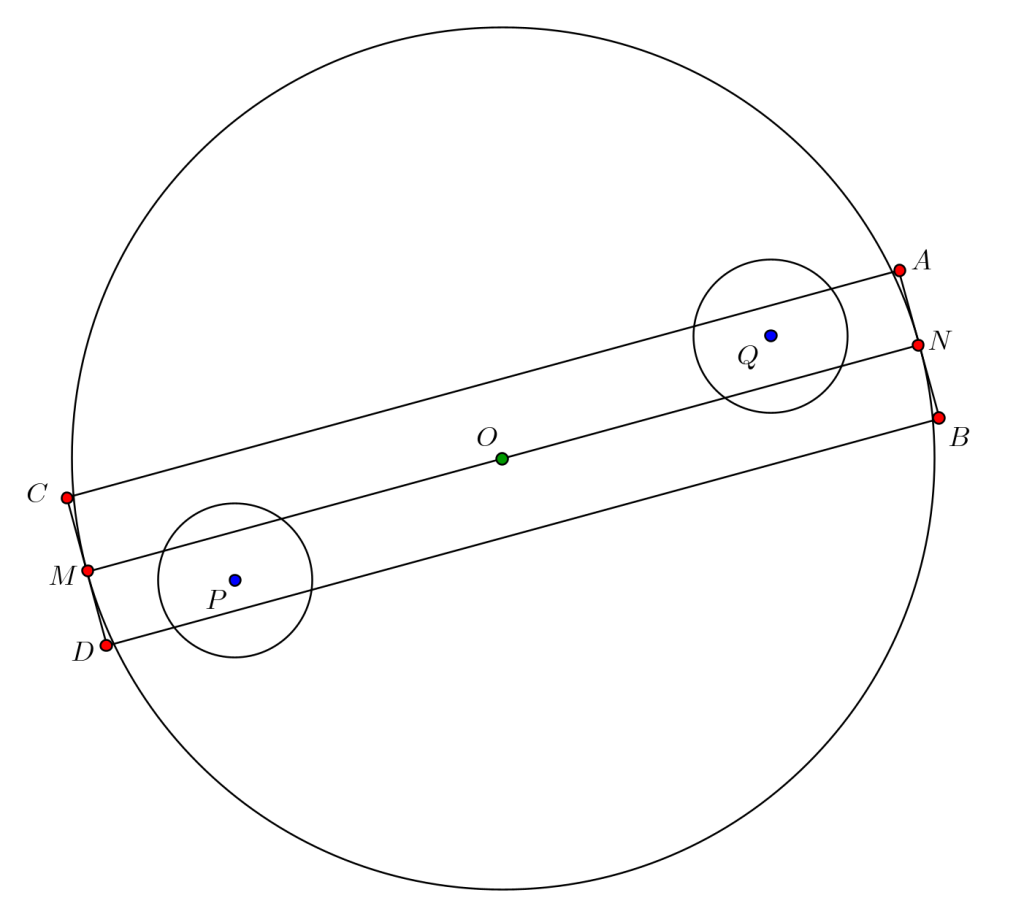
El área del rectángulo \(ABCD\) es $$AB \cdot MN = 100 \cdot 2 r = 4 \cdot 50 r > 4,$$ por la condición \(r> 1/50\). Cualquier rectángulo de área mayor que 4 centrado en el origen contiene dos puntos de coordenadas enteras en su interior (en caso contrario, su área sería inferior a cuatro). Sean \(P\) y \(Q\) dichos puntos. Las cañas de centro \(P\) y \(Q\) y radio \(r\) cortan a los segmentos \(OM\) y \(ON\), impidiendo ver la valla en esa direcciones.
Solución propuesta por Marcos Jiménez y Manuel Zambrana:
Resulta intuitivamente claro que la valla es visible desde \(O\) si y sólo si es visible desde \(O\) a través de la ventana que dejan las cañas centradas en \((0,1)\) y \((1,49)\), respectivamente, pues en ella la abertura angular es máxima y no hay obstáculos (otras cañas) que dificulten la visibilidad. Por tanto, restringimos el estudio a esta ventana.
Consideremos entonces circunferencias (cañas) \(C_1\) , \(C_2\) de de radio \(r\) y centros \((0, 1)\) y \((1, 49)\), respectivamente, como muestra la figura.
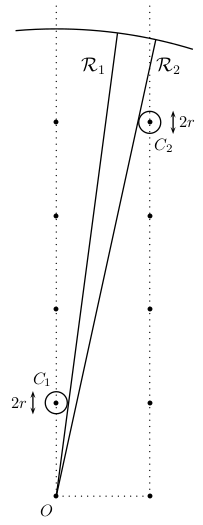
La ventana de observación es la región angular comprendida entre la recta \(R_1\) tangente a \(C_1\) y la recta \(R_2\) tangente a \(C_2\). La ventana existe si \(R_1\) tiene mayor pendiente que \(R_2\) , situación que se da siempre que \(r\) no tome valores demasiado grandes.
Lo primero que haremos será determinar la pendiente \(\lambda_1\) de \(R_1\) para un valor dado de \(r\). Consideremos temporalmente \(\lambda_1\) como un parámetro. La intersección de \(C_1\) y \(R_1\) es el conjunto de puntos \((x, y)\) que resuelven el sistema
$$\begin{cases} x^2 + (y − 1)^2 = r^2 \\ y = λ_1 x.\end{cases}$$
Para que \(R_1\) sea tangente a \(C_1\) , este sistema debe tener solución única. Eliminando \(y\), llegamos a que \(x\) satisface la ecuación
$$(1 + λ^2_1 )x^2 − 2λ_1 x + 1 − r^2 = 0.$$
Definimos los coeficientes \(a := 1+λ^2_1 , b := −2λ_1 , c := 1−r^2\). La ecuación anterior tiene solución única sólo si \(b^2 = 4ac\). Sustituyendo \(a, b, c\) por sus expresiones, encontramos que \(λ_1\) satisface la ecuación
$$r^2 λ^2_1 − 1 + r^2 = 0.$$
Para \(r\) suficientemente pequeño, la ecuación anterior tiene una solución positiva y otra negativa. La solución positiva es la que corresponde a \(R_1\). Tenemos por tant
$$\lambda_1= \frac{1-r^2}{r}.$$
El estudio de la interacción entre \(C_2\) y \(R_2\) se lleva a cabo de un modo completamente análogo. Repitiendo el mismo razonamiento de antes, llegamos a que la pendiente \(\lambda_2\) de \(R_2\) satisface
$$(1 − r^2 )λ_2^2 − 98λ + 2401 − r^2 = 0.$$
Para \(r\) suficientemente pequeño, la ecuación anterior tiene dos soluciones positivas. A \(R_2\) corresponde la mayor de ellas. Resolviendo, tenemos
$$\lambda_2=\frac{49+r\sqrt{2402-r^2}}{1-r^2}.$$
Con las expresiones de \(\lambda_1\) y \(\lambda_2\) disponemos de todo lo necesario para testear la visibilidad de la valla en función del valor que tome \(r\).
Caso 1: \(r > 1/50\)
Sustituyendo \(r = 1/50\) en \(\lambda_1\) y \(\lambda_2\), tenemos (con la mínima precisión que permite comparar las cantidades)
$$\lambda_11 \simeq 49.990, \qquad \lambda_2 \simeq 50.000.$$
Como \(\lambda_1 < \lambda_2\), la valla no es visible. Y dado que \(\lambda_1\) es una función decreciente de \(r\) y \(\lambda_2\) es una función creciente de \(r\), concluimos que la valla no es visible si \(r > 1/50\).
Caso 2: \(r < 1/ 2501\)
Sustituyendo \(r = 1/ \sqrt{2501}\), tenemos
$$\lambda_1 = 50, \qquad \lambda_2 = 50.$$
Como \(\lambda_1=\lambda_2\), las rectas \(R_1\) y \(R_2\) son la misma recta. Por tanto, el valor \(r_c := 1/ \sqrt{2501}\) representa el radio crítico que separa la región de visibilidad de la de no visibilidad. Para \(r < r_c\) la valla es visible, pues en esta región \(\lambda_1 > \lambda_2\). Para \(r > r_c\) la valla no es visible, ya que en este caso \(\lambda_1 \leq \lambda_2\). Con esto hemos terminado el análisis.

Dejar una contestacion