Los tensioactivos o surfactantes son substancias que por su composición química minimizan la tensión en la superficie de un líquido. Desde el siglo pasado se usan en una gran cantidad de productos. Sus aplicaciones se encuentran en ciencia de materiales en general y materiales nano-estructurados, química de macromoléculas, bioquímica y en la industria de cosméticos, por mencionar algunas áreas. Los tensioactivos están presentes en muchos de los detergentes que usamos para lavar la ropa, suavizantes, líquidos lavavajillas, geles de ducha, etc.
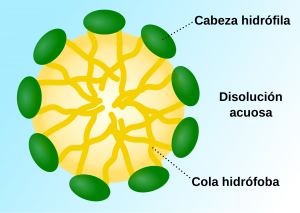
Una de sus características más especiales de los surfactantes es que tienen una naturaleza anfifílica, es decir, desde el punto de vista molecular tienen una parte (cabeza) hidrofílica (soluble en agua) y otra (cola) hidrofóbica (repelida por el agua).
Esta propiedad física es muy importante porque cuando dichas substancias se encuentran en solución acuosa pueden formar agregados coloidales conocidos como micelas que adoptan diversas formas geométricas. La estructura de estos agregados depende del tipo de surfactante, su concentración, su temperatura y la presencia de aditivos, entre otras cosas. En solución acuosa las cabezas polares apuntan hacia la fase acuosa mientras que la cola hidrofóbica apunta hacia el lado contrario de la fase acuosa tal y como se muestra en el esquema de la Figura 1.
Uno de los problemas importantes en la química de surfactantes es la determinación de los parámetros que determinan su estructura: la concentración micelar crítica (CMC) y el número de agregación. La primera es la concentración a la cual empiezan a formarse las micelas y la segunda es el número de moléculas al cual empieza la agregación que finalmente forma la estructura. Se ha determinado experimentalmente (ver, por ejemplo, [2]) que las micelas exhiben estructura esférica a concentraciones no muy alejadas de la CMC.
Hasta hace relativamente poco tiempo algunas estructuras moleculares eran caracterizadas por los químicos con conceptos geométricos que no cumplían su cometido. Un ejemplo de tales conceptos es la excentricidad \(\eta\) definida originalmente para caracterizar ciertas propiedades de las cónicas. De hecho los químicos usaban una versión tridimensional de la excentricidad, definida, para un agregado molecular, como
Esta definición tiene un problema a la hora de caracterizar la estructura molecular porque una excentricidad igual a cero corresponde a un agregado perfectamente esférico (inexistente sobre todo si se consideran sus vibraciones a lo largo del tiempo) y es igual a uno para un agregado infinitamente estirado.
Como se mencionó antes, las micelas, adoptan distintas formas geométricas y no solo esféricas. De hecho estos agregados, presentan variaciones geométricas a lo largo del tiempo que están determinadas por las posiciones promedio de las cabezas hidrofílicas. Un ejemplo se puede ver en la siguiente figura 2 que muestra las configuraciones inicial y final de una micela de 50 moléculas en disolución acuosa (de la gráfica se ha eliminado el agua para mayor claridad).

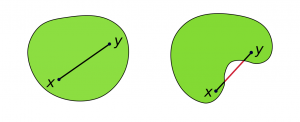
Un conjunto de puntos en un espacio euclidiano se define como convexo si contiene todos los segmentos de línea que conectan cada par de sus puntos. En la siguiente figura se muestran dos conjuntos planos, uno convexo (izquierda) y otro no (derecha):
Dado un conjunto \(M\) cualquiera (en nuestro caso nos interesará el conjunto \(M\) formado por un número finito de puntos) podemos encontrar el casco o envoltura convexa de \(M\), que no es más que la intersección de todos los poliedros convexos que contienen a \(M\). En el caso que nos interesa se sabe que dicha envoltura convexa es, en general, un poliedro convexo y que es, además, el conjunto convexo mínimo que contiene al conjunto \(M\). Más aún, se puede probar (ver el Teorema 2 de la página 33 de [1]) que los vértices de dicha envoltura convexa son algunos (no necesariamente todos) los puntos de \(M\). Todo esto nos dice que muchas de las cabezas hidrofílicas de la micela serán los vértices de la envoltura convexa del conjunto formado por todas las cabezas, lo cual es especialmente relevante a la hora de simular numéricamente la dinámica molecular.
Lo interesante de lo anterior es que hay un teorema, debido al matemático soviético Aleksandr Danilovich Alexandrov (1912-1999), que afirma que todo poliedro convexo cerrado (como los que estamos tratando) es homeomorfo a una esfera, esto es, existe una correspondencia continua uno a uno entre las dos (ver Teorema 1.7.1 pág 57 de [1]).
Basándose en el hecho de que las estructuras representadas por las cabezas micelares pueden considerarse como un poliedro convexo, y que gracias al teorema de Alexandrov son homeomorfas a una esfera, en [2], se calculó la esfericidad \(\Phi\) de todas las micelas mediante la siguiente expresión que utiliza el volumen \(V\) y el área \(A\) del poliedro:
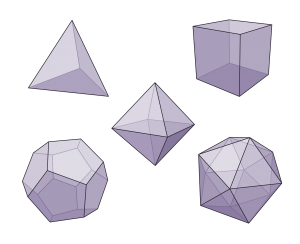
Este número \(\Phi\) da mucha más información sobre la estructura de las micelas que la excentricidad mencionada anteriormente. Para entenderlo vale la pena mencionar que la esfericidad de una esfera perfecta es 1 mientras que la esfericidad de los sólidos platónicos va de 0.671 para un tetraedro regular hasta 0.939 para un icosaedro.
En el caso de las micelas hemos de calcular la esfericidad de la envoltura convexa de sus cabezas. Este cálculo es tremendamente engorroso por lo que se ha de usar algoritmos numéricos complejos que no vamos a describir aquí. Lo que es interesante destacar es que de dichas simulaciones se pudo deducir que, para ciertos números de agregación, las micelas están formadas por estructuras esféricas en capas, como las capas de una cebolla (ver figura 5, donde se muestra una configuración de 120 cabezas de micelas).


Dejar una contestacion