Isaac Newton afirmó: “Si he visto más allá es por estar sobre los hombros de Gigantes”. Florian y Sergey nuestros héroes hoy pueden decir los mismo.
Funciones hipergeométricas
El latín fue para mí una pesadilla. Durante dos cursos teníamos 3 horas de latín a la semana. Si en vez de César con sus «guerritas» me hubieran puesto a traducir a Gauss sobre las funciones hipergeométricas o su magistral Disquisitiones Arithmeticae yo habría aprendido latín. Años más tarde lamenté no haber aprendido nada en aquellas angustiosas clases de latín. Las funciones hipergeométricas nacieron en un trabajo de Gauss de 23 páginas escrito en latín:
C. F. Gauss, Disquisitiones generales circa seriem infinitam $$ 1+\frac{\alpha\beta}{1\cdot\gamma}x+\frac{\alpha(\alpha+1)\beta(\beta+1)}{1\cdot2\cdot\gamma(\gamma+1)}xx+\frac{\alpha(\alpha+1)(\alpha+2)\beta(\beta+1)(\beta+2)}{1\cdot2\cdot3\cdot\gamma(\gamma+1)(\gamma+2)}x^3+\text{etc.}$$ Commentationes societatis regiae scientiarum Gottingensis recentiores, 2 (1813).
Más adelante Riemann asombró a todos, con sus superficies y la definición sintética de la función de Gauss. La función de Gauss está determinada por tener \(0\), \(1\), \(\infty\) como sus únicos puntos de ramificación y comportarse en ellos como las potencias \(z^\alpha\). Las propiedades de la función hipergeométrica se desprenden mágicamente de esta definición. Algo que fastidió profundamente a Weierstrass que nunca digirió las superficies de Riemann.
Después de esto no hay rama de las matemáticas que no hayan encontrado tema en las funciones hipergeométricas. El último paso son los Motivos hipergeométricos de Katz.
Debemos en primer lugar generalizar. Para nosotros una función hipergeométrica es la definida por una serie de potencias $${}_pF_q\Bigl(\begin{matrix} a_1, &\dots, & a_p\\ b_1, &\dots, & b_q\end{matrix} ; x\Bigr):=\sum_{n=0}^\infty \frac{(a_1)_n\cdots(a_p)_n}{(b_1)_n\cdots(b_q)_n}\cdot \frac{x^n}{n!},$$ donde \((a)_n:= a(a+1)\cdots(a+n-1)\).
Primero los gigantes
Ya Gauss notó que en algunos casos su función era algebraica. Por ejemplo Gauss escribe $$(t+u)^n+(t-u)^n=2t^n{}_2F_1(-\tfrac{n}{2},\tfrac{1-n}{2};\tfrac12; \tfrac{u^2}{t^2}),$$ es decir $${}_2F_1(-\tfrac{n}{2},\tfrac{1-n}{2};\tfrac12; x)=\frac{(1+\sqrt{x})^n+(1-\sqrt{x})^n}{2}.$$ Herman Schwarz en 1873 resuelve el problema de cuando la función de Gauss \({}_2F_1([\alpha,\beta],[\gamma],x)\) es una función algebraica de \(x\). Schwarz era un matemático al que le gustaban los problemas concretos, obteniendo la solución mediante técnicas que después otros generalizaron. Es en este trabajo en el que construye la función modular mediante la transformación conforme de un triángulo con lados arcos de circunferencia en un semiplano. A cada función hipergeométrica Schwarz asocia un triplete de números \((\lambda,\mu,\nu)=(1-\gamma,\gamma-\alpha-\beta,\alpha-\beta)\) y da una lista de tripletes de números, de forma que \({}_2F_1([\alpha,\beta],[\gamma],x)\) es algebraica (suponiendo que \(\lambda\), \(\mu\), \(\nu\notin \mathbb Z\)) si y solo si \((\lambda,\mu,\nu)\) o alguna permutación, cambio de signo o suma de triplete de enteros con suma par, aparece en la lista.

Aparte de matemático, Schwarz era el jefe de la Brigada de Bomberos Voluntarios y ayudaba al jefe de la estación de trenes a abrir y cerrar las puertas de los trenes.
Ya llevamos tres gigantes, Gauss, Riemann y Schwarz, el siguiente gigante es Gotthold Eisenstein quien demostró un teorema sobre las series de potencias que definen una función algebraica, que después fue refinado por Heinrich Eduard Heine.
Teorema (Eisenstein 1852, Heine 1853). Si una serie de potencias \(f(x)\in \mathbb Q[[x]]\) es una función algebraica, entonces existe un entero no nulo \(M\) tal que \(f(Mx)-f(0)\in \mathbb Z[[x]]\).
En particular los coeficientes de una serie de potencias racional que sea función algebraica contienen solo un número finito de primos en sus denominadores.
Diremos que \(f\) es casi entera si \(f\) es una serie de potencias que cumple el criterio de Eisenstein.
Edmund Landau en 1904 y 1911 usa el teorema de Eisenstein para obtener una condición necesaria para que la función hipergeométrica de Gauss sea algebraica.
Teorema (Landau). Sea \(F(x)={}_2F_1(\alpha,\beta;\gamma;x)\) tal que \(\alpha\), \(\beta\), \(\gamma\), \(\alpha-\gamma\) y \(\beta-\gamma\) no sean enteros. Sea \(N\) el común denominador de los números \(\alpha\), \(\beta\) y \(\gamma\). Entonces \(F\) satisface la condición de Eisenstein si y solo si para cada \(1\le \lambda\le N\) relativamente primo con \(N\), se tiene $$\langle \lambda \alpha\rangle<\langle \lambda \gamma\rangle<\langle \lambda \beta\rangle \quad \text{o}\quad \langle \lambda \beta\rangle<\langle \lambda \gamma\rangle<\langle \lambda \alpha\rangle,$$ donde \(\langle x\rangle\) denota la parte fraccionaria de \(x\).
Alfred Errera en 1913 prueba que la condición de Landau equivale a la clasificación de Schwarz. Es decir la condición de Landau es también suficiente para que la función de Gauss sea algebraica.
Extensión a funciones hipergeométricas generalizadas
Gauss y Schwarz, Eisenstein y Heine, y Landau, Errera completan el estudio de cuando la función hipergeométrica de Gauss es algebraica. Nuevos matemáticos retoman el tema para las funciones hipergeométricas generalizadas.
El caso de las funciones hipergeométricas generalizadas fue considerado por Gilles Christol en 1986, quien consigue extender los resultados de Landau. En poco tiempo el problema es resuelto completamente, por Frits Beukers y Gert Heckman para $${}_pF_q([a_1,\dots,a_p]; [b_1,\dots b_q];x)$$ cuando los coeficientes \(a_j\), \(b_k\in \mathbb Q\) son racionales para todo \(j\) y \(k\) y \(a_j\), \(a_j-b_k\notin\mathbb Z\).
El criterio se refiere a una serie de potencias $$F(x)={}_pF_{p-1}\Bigl(\begin{matrix} a_1, &\dots, & a_p\\ b_1, &\dots, & b_{p-1}\end{matrix} ; x\Bigr)$$ con \(a_1\), . . . , \(a_p\), \(b_1\), . . . , \(b_{p-1}\in \mathbb Q\smallsetminus (-\mathbb N)\) y dice los siguiente
Teorema (Christol, Beukers, Heckman, Katz). Sea \(F(x)\) la función indicada arriba. Supongamos que \(a_j\), \(a_j-b_k\notin\mathbb Z\) para todo \(j\), \(k\). Sea \(N\) el menor común denominador de los parámetros. Entonces \(F\) es algebraica si y solo si los números \(A=\{e^{2\pi i \lambda a_1},\dots, e^{2\pi i \lambda a_p}\}\) y los \(B=\{e^{2\pi i \lambda b_1},\dots, e^{2\pi i \lambda b_{p-1}}, e^{2\pi i \lambda}\}\) alternan en la circunferencia unidad para todo \(1\le \lambda\le N\) con \(\mathop{\rm mcd}(\lambda,N)=1\).
Con estos resultados el problema está esencialmente resuelto. La solución es comparable a una escultura griega o una sonata de Beethoven. Las funciones hipergeométricas se extienden a todo el plano complejo excepto por tres singularidades \(0\), \(1\), \(\infty \).
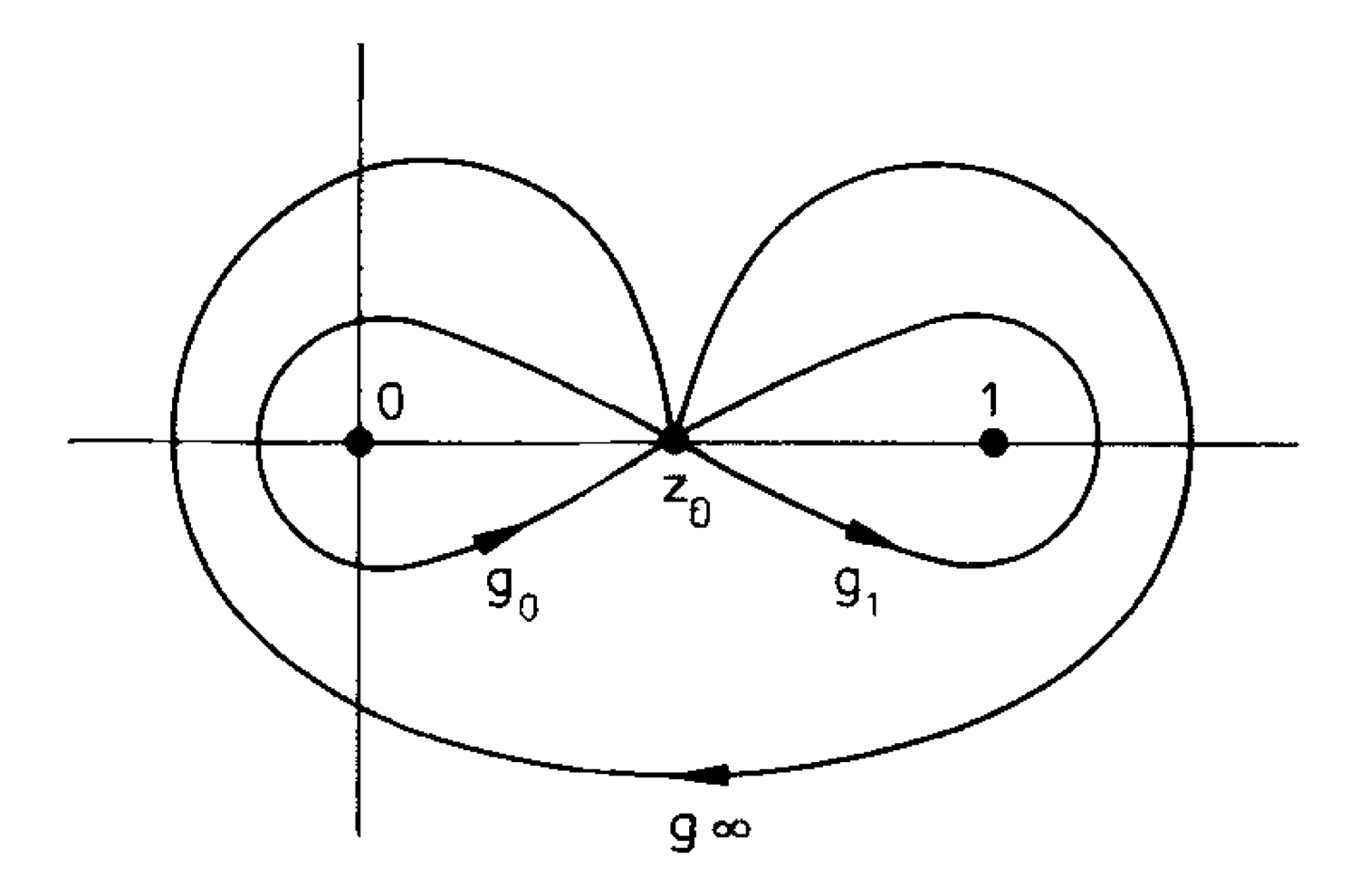
Riemann ya entendió que la pieza fundamental es el grupo de monodromía. Cada curva cerrada que comienza en un punto regular \(z_0\) y vuelve a él sin pasar por las singularidades intercambia las diversas ramas de la función hipergeométrica. Lo que determina un grupo. La parte esencial de la solución está contenida en el trabajo de Frits Beukers y Gert Heckman y consiste en determinar exactamente el grupo de monodromía de la función \({}_nF_{n-1}(x)\) en función de los parámetros. La función es algebraica si y solo si el grupo es finito. Estos grupos finitos generados por reflexiones en \(\mathbb C^n\) ya estaban determinados. Resulta que estos casos de funciones algebraicas son como accidentes, resultando, esencialmente, en un número finito de casos en cada dimensión \(n\). Funciones con una simetría increíble, semejante a los poliedros regulares en cada dimensión.
El problema restante
Y llegamos al objeto de nuestra entrada hoy. Como observan Florian Fürnsinn y Sergey Yurkevich, las hipótesis de racionalidad de los parámetros hechas en el criterio de anterior no están justificadas, ellos ponen el ejemplo $${}_3F_2\Bigl(\begin{matrix} 1/2& \sqrt{2}+1& -\sqrt{2}+1\\ \sqrt{2} & -\sqrt{2} &\end{matrix}; 4x\Bigr)=\frac{(7x-1)(2x-1)}{(1-4x)^{5/2}}=1+x-6x^2+\cdots\in\mathbb Z[[x]],$$ cuyos parámetros no son racionales y es una función algebraica. También la función $${}_2F_1\Bigl(\begin{matrix} 2 & 2\\ 1& \end{matrix}; x\Bigr)=\frac{(1+x)}{(1-x)^3},$$ es algebraica, pero no se aplica el criterio de Beukers-Heckman ya que hay diferencias enteras entre sus parámetros.
Florian y Sergey proporcionan un algoritmo que decide si una función hipergeométrica es algebraica o no cualquiera que sean sus parámetros.
Para hablar de su algoritmo es conveniente considerar series de potencias $$\mathcal F(x)=\mathcal F\Bigl(\begin{matrix} a_1, &\dots, & a_r\\ b_1, &\dots, & b_s\end{matrix} ; x\Bigr)=\sum_{n=0}^\infty \frac{(a_1)_n\cdots (a_r)_n}{(b_1)_n\cdots (b_s)_n}x^n$$ La función hipergeométrica se diferencia en que uno de los \(b_j=1\).
Decimos que \(\mathcal F\) es reducida si para todo par \((j,k)\), tenemos \(a_j-b_k\notin\mathbb Z\). Y decimos que \(\mathcal F\) es contraída si \(a_j-b_k\notin\mathbb N\).
A cada función \(\mathcal F\) le asociamos su contraída \(\mathcal F^c\). Esta se obtiene, tomando de todas las diferencias \(a_j-b_k\in \mathbb N\) una con valor mínimo \(a_{j_0}-b_{k_0}\) y eliminando esta pareja de índices. Repitiendo esta operación hasta que obtengamos una \(\mathcal F^c\) que sea contraída. Por ejemplo, en el caso anterior $${}_3F_2\Bigl(\begin{matrix} 1/2& \sqrt{2}+1& -\sqrt{2}+1\\ \sqrt{2} & -\sqrt{2} &\end{matrix}; x\Bigr)=\mathcal F\Bigl(\begin{matrix} 1/2& \sqrt{2}+1& -\sqrt{2}+1\\ \sqrt{2} & -\sqrt{2} &1\end{matrix}; x\Bigr)$$ se transforma sucesivamente en $$\mathcal F\Bigl(\begin{matrix} 1/2& \sqrt{2}+1\\ \sqrt{2} &1\end{matrix}; x\Bigr)$$ $$ \mathcal F\Bigl(\begin{matrix} 1/2& & \\ 1\end{matrix}; x\Bigr)={}_1F_0\Bigl(\begin{matrix} 1/2&\\ \{\}\end{matrix}; x\Bigr)=(1-x)^{-1/2}.$$ Otro ejemplo $${}_2F_1\Bigl(\begin{matrix} 1/2 & 2\\ 3/2 & \end{matrix};x\Bigr)=\mathcal F \Bigl(\begin{matrix} 1/2 & 2\\ 3/2 & 1\end{matrix};x\Bigr)\to\mathcal F \Bigl(\begin{matrix} 1/2 \\ 3/2\end{matrix};x\Bigr)={}_2F_1\Bigl(\begin{matrix} 1/2 & 1 \\ 3/2& \end{matrix};x\Bigr)$$ que es contraída pero no reducida.
El resultado básico de Florian y Sergey es que \(\mathcal F\) es algebraica si y solo si su contraída es algebraica. Con estos elementos podemos describir su algoritmo
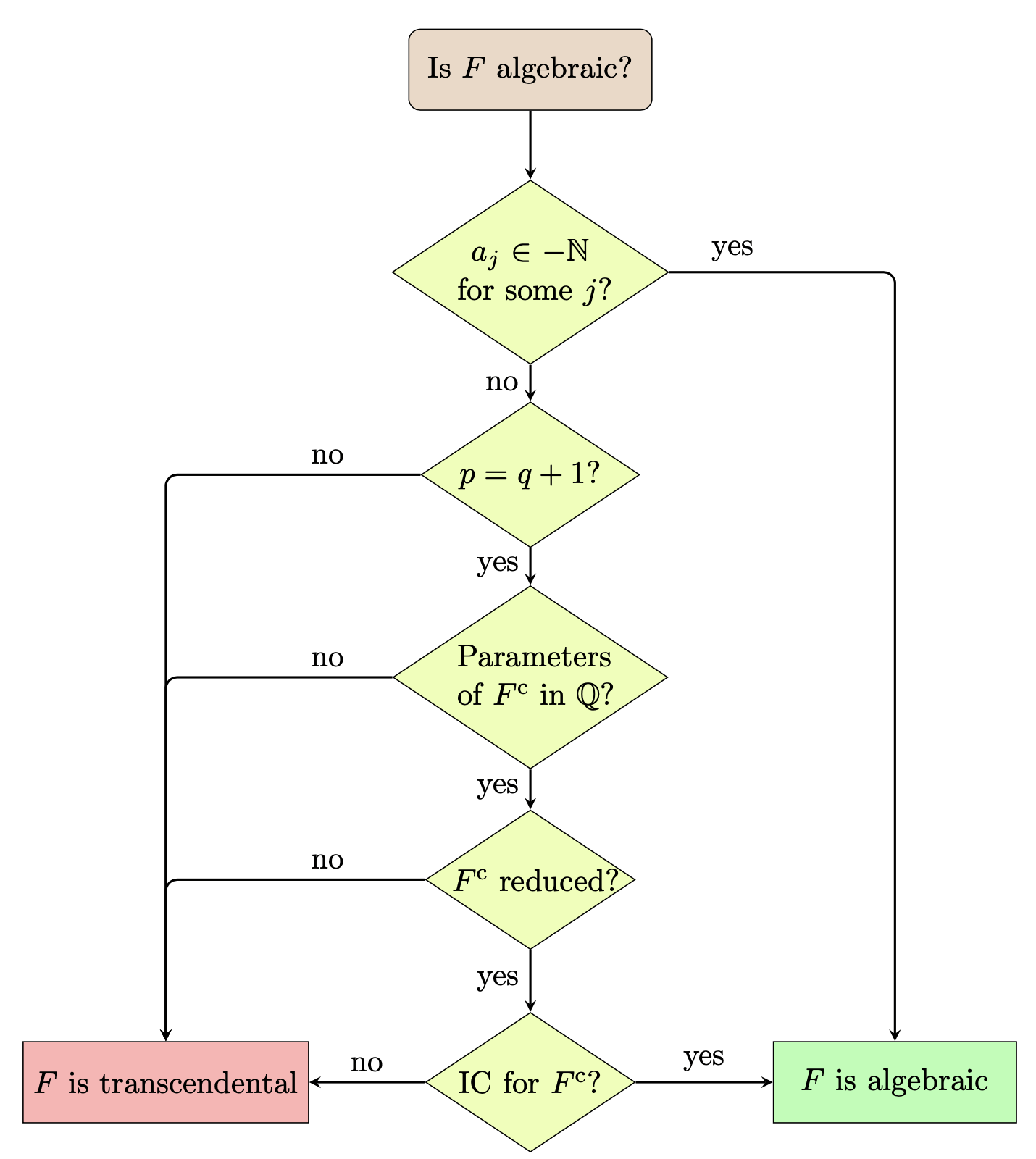
Si alguno de los \(a_j\in -\mathbb N\) la función es un polinomio. Una función hipergeométrica \({}_pF_q(x)\) solo puede ser algebraica si \(p=q+1\). Una función contraída y algebraica tiene que tener los parámetros racionales y ser reducida. Finalmente, para una función que ha llegado hasta este punto es algebraica si y solo satisface el criterio de alternancia de las raíces de la unidad de Beukers-Heckman.
Florian es alumno de doctorado en la Universidad de Viena y Sergey está de PostDoc en la misma Universidad. Los dos han trabajado para su tesis con el Profesor Herwig Hauser, cuya página web merece una visita. Yo no me perdería su Galeria de singularidades, que desde luego he conocido a través de esta entrada.


Ira Gessel y sus paseos
Ira Gessel es un matemático que trabaja en combinatoria. En 2001 consideró el problema de los paseos en el primer cuadrante \(Q:=\{(x,y)\colon x, y\ge 0\}\) comenzando en el origen y terminando en el origen con pasos \(i\), \(-i\), \(1+i\) y \(-1-i\). Hay que tener en cuenta que estos pasos no están permitidos si nos llevan fuera de \(Q\). Gessel observó que el número de paseos de longitud \(m\) es cero si \(m\) es impar y cuando \(m=2n\) es par, entonces $$g_{2n}=16^n \frac{(5/6)_n(1/2)_n}{(5/3)_n(2)_n},\qquad n\ge0.$$ Pero esto no era más que una observación. La conjetura es equivalente a decir que $$\sum_{n=0}^\infty g_n x^n= {}_3F_2\Bigl(\begin{matrix}5/6 & 1/2 & 1\\5/3 & 2 & \end{matrix}; 16x^2\Bigr).$$ Manuel Kauers, Christoph Koutschan y Doron Zeilberger probaron en 2008 la conjetura con la ayuda de ordenadores. Ellos encuentran una recurrencia para \(g_n\), la recurrencia expresa \(g_{n+32}\) en términos de \(g_{n+j}\) con \(0\le j<32\) y coeficientes que son polinomios en \(n\) de grado 172, donde intervienen enteros de 385 dígitos. La prueba consiste entonces en ver que la fórmula imaginada por Gessel satisface esta recurrencia y que los primeros 32 valores coinciden. Este trabajo fue publicado en los prestigiosos Proceedings of the National Academy of Science de USA.
En 2015 Alin Bostan, Irina Kurkova y Kilian Raschel publicaron su artículo A human proof of Gessel’s lattice path conjecture.
Bien, la función \(\sum_{n=0}^\infty g_nx^n\) es algebraica, pero esto no fue observado hasta el año 2010. El criterio de Beukers y Heckman no se aplica directamente ya que hay diferencias enteras entre sus parámetros. Lo que hace ver el interés del trabajo de Florian y Sergey. Ya no habrá más funciones hipergeométricas algebraicas sin detectar.
Hablando de Ira Gessel, no podemos dejar de mencionar su papel en el libre derecho a ciertas necesidades fisiólogicas. Ver también.
Final
Florian y Sergey conocían el ejemplo de los paseos de Gessel y otros en que el criterio de Beukers-Heckman no se aplicaba. Trabajando en estos temas sobre las series de potencias y su algebraicidad era natural que se plantearan el problema.
«Relativamente pronto encontramos cómo deberías ser el criterio y también las ideas principales se agruparon pronto. Sin embargo los argumentos precisos que encontramos de algunas afirmaciones eran técnicas y más complicadas que lo que pensábamos, pero en conjunto disfrutamos el trabajo. Estabamos compartiendo un despacho en aquél momento, y fue una agradable experiencia tener un proyecto común»
Para saber más
El artículo que celebramos hoy se encuentra en arXiv:
No es difícil de leer, aunque naturalmente usa los resultados de los artículos anteriores. Especialmente interesante es sin duda
que podemos descargar de algunos sitios en la web. También el articulo de Schwartz se encuentra libremente en la red. La dificultad del alemán es ahora más ligera con los métodos actuales de traducción
Hermann Amandus Schwarz, Ueber diejenigen Fälle, in welchen die Gaussische hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt, J. Reine Angew. Math. 75 (1873), 292-335. [Cuidado descarga el volumen entero de la revista]
Como ha evolucionado el tema desde Gauss hasta la teoría de motivos podemos verlo en el artículo de Rodríguez Villegas en el Notices of the American Mathematical Society.
Un material relacionado muy intrigante es la conferencia de Sergey Yurkevich en el Institue de Hautes Études Scientifiques «How to conjecture and prove that the generating function of the Yang-Zagier numbers is algebraic«.
La imagen destacada hoy son flores en un estanque, la simetría de estas flores semejan las simetrías que representan las funciones hipergeométricas algebraicas.


Dejar una contestacion