Lax, Milgram, Babuska y Lions

Peter David Lax (nacido en 1926 en Budapest, Hungría) es un conocido matemático que ha realizado importantes contribuciones a la mecánica de fluidos y al análisis teórico y numérico de las EDP. Tienen especial relevancia sus aportaciones al estudio de los sistemas hiperbólicos de leyes de conservación, véanse [1,2]; véase también [3]. Es profesor del Departamento de Matemáticas del prestigioso Courant Institute en la Universidad de Nueva York. Fue premiado con la National Medal of Science en 1986, el Premio Wolf en 1987 y el Premio Abel en 2005.

Ivo M. Babuska (1926-2023) fue un matemático checo-estadounidense, conocido por sus aportaciones al análisis teórico y numérico de las EDP, en particular, en el ámbito de los métodos de elementos finitos.

Uno de los resultados más conocidos en el campo de los elementos finitos es la llamada condición de Babuska-Brezzi (también llamada condición de Babuska-Brezzi-Ladyzhenskaya o condición inf-sup), deducida de manera independiente por él y por el matemático italiano Franco Brezzi; véase [5,6]. Se trata de una condición suficiente para la estabilidad de problemas mixtos. Ha permitido calcular aproximaciones numéricas eficientes de problemas tan importantes desde un punto de vista práctico como los de Darcy, Stokes y Navier-Stokes.

Desde 1968 hasta 1996 fue profesor en la Universidad de Maryland. Posteriormente, ocupó la Cátedra Robert B. Trull de Ingeniería de la Universidad de Texas en Austin. Recibió ente otros el Premio de Matemáticas del estado checoslovaco, el Premio Birkhoff, el Premio Humboldt de la República Federal de Alemania y la Medalla de Bolzano.

Babuska es también conocido por ser el autor de una generalización del Teorema de Lax-Milgram, conocida como Teorema de Babuska-Lax-Milgram, que permite ampliar la familia de EDP resolubles incluyendo, por ejemplo, sistemas no escalares donde las ecuaciones son de distinto orden. Como aplicación, vemos que este resultado hace posible en un fluido viscoso asignar a cada campo de fuerzas externas un campo de velocidades y una presión; más detalles aparecen en la Sección 4.

Jacques-Louis Lions (1928-2001) fue un matemático francés de enorme influencia en su época. Contribuyó de manera relevante al análisis de las EDP y a la teoría de control e impulsó con gran intensidad y éxito el uso de las Matemáticas en la industria. Fue profesor en la Universidad de Nancy, en la Facultad de Ciencias de la Universidad de París 6, en la École Polytechnique y en el Collège de France. Fue Director del Institut National de la Recherche en Informatique et Automatique y posteriormente del Centre National d’Études Spatiales. Fue galardonado con el Premio SIAM John von Neumann en 1986 y con el Japan Prize, compartido con John Julian Wild, en 1991. De 1991 a 1999 presidió la Unión Matemática Internacional y gracias a él el año 2000 fue declarado por la UNESCO «Año Internacional de las Matemáticas».

Una de sus muchas contribuciones fue una nueva generalización del Teorema de Lax-Milgram, conocida como Teorema de Lions-Lax-Milgram o simplemente Teorema de Representación de Lions que hace posible (también) la resolución de EDP de evolución con datos no regulares. Así, gracias a este resultado, podemos hablar de la evolución a lo largo de un intervalo temporal de la distribución de temperatura en un medio no homogéneo sometido a una fuente de calor. Más detalles aparecen en la sección siguiente.

El Teorema de Lax-Milgram es tal vez el resultado más significativo y útil en el contexto de las EDP. Permite «resolver» una gran cantidad de problemas con origen diverso y dar un sentido a las soluciones asociadas; véase por ejemplo [7,8].

El enunciado no es complicado:

Teorema: Se suponen dados un espacio de Hilbert \(V\), una forma bilineal \(m(\cdot\,,\cdot) : V \times V \mapsto {\bf R}\) y una forma lineal \(\ell : V \mapsto {\bf R}\). Se supone que la forma bilineal es continua y coercitiva (esto último significa que existe \(\alpha > 0\) tal que \(m(v,v) \geq \alpha \| v \|^2\) para todo \(v \in V\)) y que la forma lineal \(\ell\) es continua, es decir, \(\ell \in V’\). Entonces existe un único \(u\) que verifica

$$m(u,v) = \langle \ell,v \rangle \quad \forall v \in V, \quad u \in V.$$

Además, \(u\) depende continuamente de \(\ell\).

Por ejemplo, este resultado conduce a la existencia y unicidad de solución (en un sentido adecuado) de EDP de la forma

$$- \sum_{i=1}^N \partial_i (a({\mathbf x}) \partial_i u) + c({\mathbf x}) u = f({\mathbf x})$$

en un abierto acotado \(\Omega \subset {\bf R}^N\) con \(f \in L^2(\Omega)\), las funciones \(a\) y \(c\) tan sólo en \(L^\infty(\Omega)\) con \(a({\mathbf x}) \geq a_0 > 0\) y \(c({\mathbf x}) \geq 0\) en casi todo, complementada con condiciones sobre la frontera \(\partial\Omega\) (por ejemplo, tiene sentido pedir que \(u = 0\) sobre \(\partial\Omega\)).

Obsérvese que, si \(a\) y/o \(c\) son (por ejemplo) constantes a trozos, no tiene sentido hablar de soluciones en un sentido clásico.

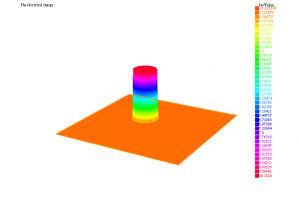
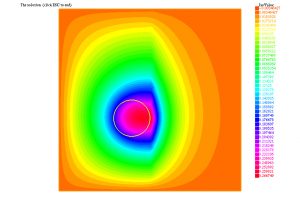
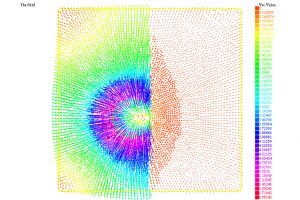
Si \(c({\mathbf x}) = 0\), se puede interpretar que \(f\) es una distribución de carga eléctrica, repartida a lo largo y ancho de un material dieléctrico no homogéneo y que \(u\) es el potencial eléctrico generado. De acuerdo con ello, el campo eléctrico asociado está dado por \({\mathbf E}({\bf x}) = – \kappa \, a({\bf x}) \nabla u({\bf x})\) para una constante positiva \(\kappa\). Gracias al Teorema de Lax-Milgram, sabemos que el modelo «produce» un campo eléctrico incluso si las propiedades del material cambian drásticamente de un punto a otro; véanse las Fig. 4-6.

La condición de coercitividad de \(m(\cdot\,,\cdot)\) es suficiente pero no necesaria para la existencia y unicidad de solución. En realidad, la conclusión del teorema precedente sigue siendo válida cuando se cumple esta otra hipótesis, debida a Babuska:

$$ \inf_{u \in V}\sup_{v \in V} \, \frac{m(u,v)}{\|u\|_V\|v\|_V} > 0 \ \ \hbox{ y } \ \ \sup_{u \in V} \, m(u,v) > 0 \ \ \ \forall v \not= 0.$$

Esto se comprende fácilmente cuando se analiza el resultado en dimensión finita, esto es, con \(m(u,v) = Mu \cdot v\), siendo \(u\) y \(v\) vectores-columna y \(M\) una matriz cuadrada no necesariamente simétrica. Este segundo resultado recibe usualmente el nombre de Teorema de Babuska-Lax-Milgram.

Una conocida consecuencia es la existencia y unicidad de solución del problema de Stokes, que puede formularse así: hallar \(({\bf u},p) \in X \times Y\) tal que

$$ \left\{
\begin{array}{l}\displaystyle
\int_\Omega \nabla{\bf u}:\nabla{\bf v} \,d{\bf x}
– \int_\Omega p \ (\nabla\cdot{\bf v}) \,d{\bf x} = \int_\Omega {\bf f}\cdot{\bf v} \,d{\bf x} \ \ \forall {\bf v} \in X , \\ \\ \displaystyle\int_\Omega q \ (\nabla\cdot{\bf u}) \,d{\bf x} = 0 \ \ \forall q \in Y,
\end{array}\right.$$

donde \(X\) y \(Y\) son espacios de Hilbert a los que respectivamente pertenecen campos de velocidades y presiones que describen el comportamiento de un fluido.

Se puede ir más lejos. Más precisamente, se puede aceptar que la forma bilineal está definida en \(V \times W\), donde (de nuevo) \(V\) es un espacio de Hilbert y \(W\) es un espacio normado (no necesariamente completo). Se tiene entonces el resultado siguiente, conocido como Teorema de Lions-Lax-Milgram:

Teorema: Se supone que la forma bilineal \(m(\cdot\,,\cdot) : V \times W \mapsto {\bf R}\) es continua. Entonces las siguientes afirmaciones son equivalentes:

Este resultado permite resolver (por ejemplo) la EDP de evolución

$$ u_t – \sum_{i=1}^N \partial_i (a({\mathbf x}) \partial_i u) + c({\mathbf x}) u = f({\mathbf x},t) $$

en un abierto de la forma \(\Omega \times (0,T)\) con \(T > 0\), de nuevo complementada con condiciones adecuadas.

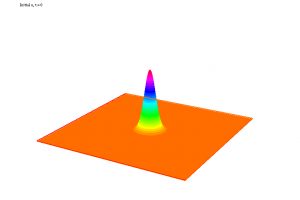
Aquí, podemos interpretar que \(u = u({\bf x},t)\) es la temperatura de un medio que evoluciona a partir de un estado inicial en el tiempo \(t = 0\) y está sometida a los efectos de una fuente de calor \(f\) durante todo el intervalo \((0,T)\). De nuevo, aceptamos la posibilidad de que el medio no sea homogéneo y, en consecuencia, los coeficientes \(a\) y \(c\) presenten discontinuidades. Una ilustración gráfica aparece en las Fig. 7-9.

El Teorema de Lions-Lax-Milgram también permite resolver problemas no estacionarios formulados en dominios espaciales que cambian con el tiempo; véase por ejemplo [9,10]. Una aplicación interesante es el modelado de la evolución de la temperatura del hielo que cubre los casquetes polares. Encontramos otra aplicación cuando tratamos de ver cómo evoluciona la densidad de células cancerígenas en un tumor cuyo tamaño cambia en el  tiempo.

El resultado también es útil cuando tratamos de determinar (por ejemplo) la población de peces en un recinto que se ve afectado por el ciclo de la marea.