Publicamos la solución al divertimento de la preparación de la maratón. Muchas gracias a Renato Álvarez Rodríguez y Niurka Rodríguez Quintero, F. Damián Aranda Ballesteros, Don Diedro y Don Pablo, Juan Miguel Expósito, Magdalena Jáñez Vaz, Marcos Jiménez Belenguer y Manuel Zambrana Ramírez, Antonio Medinilla Garófano y David Ramos Orozco y Ana Ruiz López, por las soluciones que nos han enviado. Se ha recibido una solución incorrecta.
Divertimento
En un momento dado, los corredores que tomaban parte en una carrera se extendían a lo largo de un kilómetro de longitud. El organizador le había pedido a dos ayudantes que se encontraban al final del grupo de corredores que le avisaran cuando el último corredor hubiera pasado por un punto concreto. Cuando esto ocurrió, uno de los ayudantes fue corriendo a donde estaba el organizador, le avisó y después regresó de vuelta a la cola del pelotón, llegando justo al lugar donde se encontraba el organizador cuando el ayudante empezó su carrera.
Cuando se encontró con el primer ayudante, este le dijo: “La verdad es que no has corrido mucho”.
¿Qué distancia recorrió el segundo ayudante, teniendo en cuenta que su velocidad y la de todos los corredores eran constantes?
Fe de erratas
Aunque en el vídeo sí se dice, en el enunciado faltó incluir la última condición: que el segundo ayudante se reencontró con el primero en el lugar donde se encontraba el organizador cuando aquel inició su recorrido. Ha pasado inadvertido hasta hace unos días, y ya era demasiado tarde para cambiarlo. Por tanto, hemos dado por válidas todas las respuestas que han razonado correctamente sin conocer el último dato. Pedimos nuestras más sinceras disculpas a nuestros lectores, especialmente a aquellos que no hayan sido capaces de mandar una solución por desconocer la hipótesis.
Solución
Llamemos \(v_p\) a la velocidad del pelotón, expresada en kilómetros por cierta unidad de tiempo, y \(v_a\) a la del segundo ayudante. Este se movió a una velocidad relativa \(v_a-v_p\) respecto a la cabeza de carrera hasta llegar al organizador, y después a una velocidad relativa \(v_a+v_p\) hasta volver al coche escoba. Por tanto, tardó \(1/(v_a-v_p)+1/(v_a+v_p)\) unidades de tiempo en hacer ese recorrido. En ese tiempo, el pelotón recorrió un kilómetro exacto, así que
$$\frac{1}{v_a-v_p}+\frac{1}{v_a+v_p}=\frac{1}{v_p}.$$
Llamemos \(q=v_a/v_p>1\). Notemos que es justo la distancia que recorrió el segundo ayudante durante el tiempo \(1/v_p\). Para finalizar, podemos simplificar la expresión anterior y obtener que \(q^2-2q-1=0\), de donde necesariamente \(q=1+\sqrt{2}\) kilómetros.
Todos quienes han dado con la solución (teniendo en cuenta el comentario de la fe de erratas) han seguido un razonamiento similar al anterior. Sin embargo, Marcos Jiménez y Manuel Zambrana nos han enviado además una solución alternativa de carácter más geométrico muy interesante. La reproducimos a continuación:
Usaremos el siguiente diagrama espacio-tiempo:
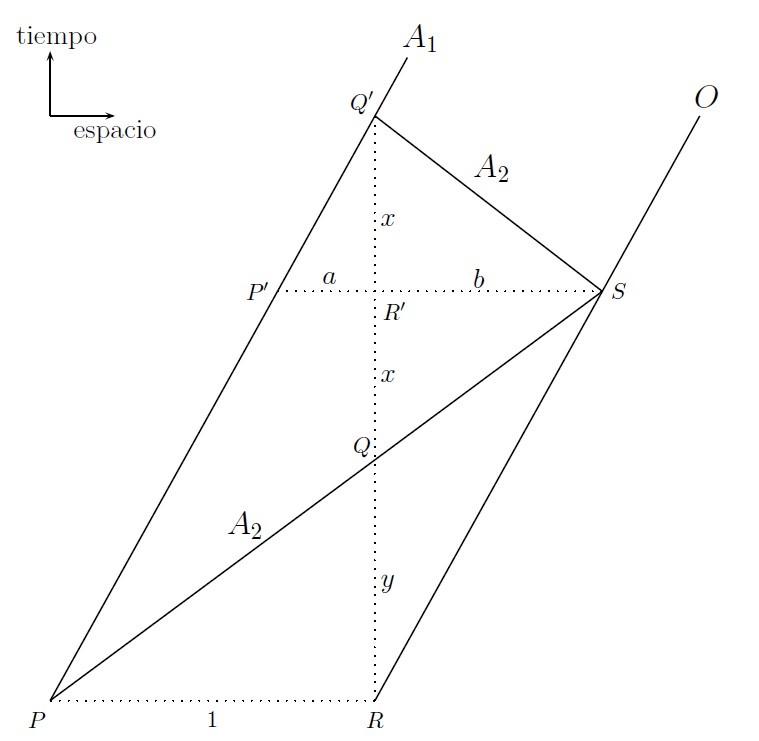
La figura da cuenta de la historia espacio-temporal de los ayudantes \(A_1\), \(A_2\) y el organizador \(O\). La dirección vertical es el tiempo y la horizontal, el espacio. A los puntos del diagrama los llamaremos genéricamente sucesos.
Las historias de \(A_1\) y \(O\) son rectas paralelas (pues ambos se desplazan con la misma velocidad) que distan horizontalmente un kilómetro. En el suceso \(P\), \(A_2\), que coincide en \(P\) con \(A_1\), parte en busca de \(O\), alcanzándolo en el suceso \(S\). Tras ello regresa a su posición de partida, reuniéndose con \(A_1\) en el suceso \(Q’\).
Dicho suceso queda fijado por la hipótesis de que el reencuentro de \(A_1\) y \(A_2\) se produce en el mismo punto del espacio que ocupaba \(O\) en el momento en el que \(A_2\) salía en busca de \(O\). El suceso \(S\) queda fijado de modo que las pendientes de \(PS\) y \(SQ’\) sean iguales (salvo signo), pues sabemos que \(A_2\) se mueve con velocidad constante. De aquí se sigue que el triángulo \(QQ’S\) es isósceles. La unicidad de la solución es manifiesta sobre la base del diagrama.
Entre \(P\) y \(S\), \(A_2\) recorre la distancia \(1+b\). Entre \(S\) y \(Q’\), recorre la distancia \(b\). Por tanto, la distancia total recorrida será \(d_T=1+2b\). La variable que tenemos que calcular es \(b\). Tenemos las siguientes ecuaciones:
$$a+b=1,\qquad\qquad\quad\;\, (1)\\
\frac{x}{a}=\frac{2x+y}{1},\qquad\qquad (2)\\
\frac{y}{1}=\frac{x}{b}.\qquad\qquad\quad\quad\; (3)$$
La ecuación \((1)\) es consecuencia de que entre \(A_1\) y \(O\) media un kilómetro en cualquier instante de tiempo. La ecuación \((2)\) se sigue de la semejanza de los triángulos \(PQ’R\) y \(P’Q’R’\), y la \((3)\), de la semejanza de \(PQR\) y \(QR’S\). Las ecuaciones \((2)\) y \((3)\) tienen soluciones \((x,y)\) no triviales si y solo si \(2ab+a-b=0\). De \((1)\) se sigue que \(a=1-b\). Sustituyendo en la última igualdad y simplificando, obtenemos la ecuación \(2b^2-1=0\), que tiene la solución positiva \(b=\sqrt{2}/2\), y con ello, \(d_T=1+2b=1+\sqrt{2}\) kilómetros.

Dejar una contestacion