Publicamos la solución al divertimento de pi y el choque de masas. Muchas gracias a Renato Álvarez Rodríguez y Niurka Rodríguez Quintero, Marcos Jiménez y Manuel Zambrana, Antonio Medinilla Garófano y David Ramos Orozco y Ruben Ríos Mallqui por las soluciones que nos han enviado. Se ha recibido una solución parcialmente correcta de Ángela Colón Ibáñez y Pablo Montero Moreno.
Divertimento
Sea \(S\) la circunferencia de radio uno y origen el punto \((0,0)\), y sea \(P_1=(-1,0)\). Se considera un número entero positivo \(n\) y se traza la recta \(r_1\), que pasa por \(P_1\) y tiene pendiente \(m=-10^n\). La recta \(r_1\) corta a \(S\) en un punto \(P_2\). Sea ahora \(P_3\) el punto simétrico de \(P_2\) respecto del eje horizontal, y \(r_2\) la recta que pasa por \(P_3\) con pendiente \(m\).
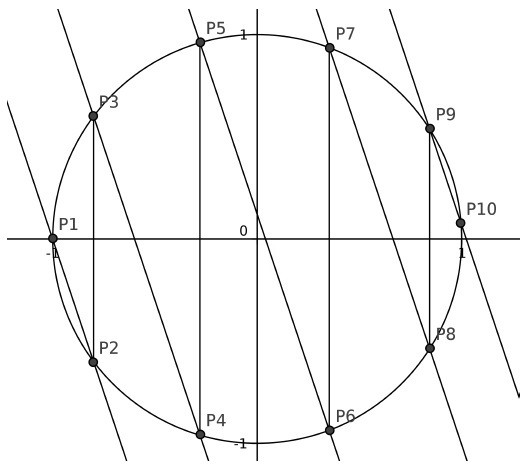
Esta construcción se puede iterar hasta obtener un punto \(P_{N+1}\) con dos coordenadas positivas y la primera mayor que la segunda, de modo que \(N\) coincide con el número de segmentos de la forma \(P_iP_{i+1}\) en el interior de la circunferencia. Se pide:
- Determina el número de segmentos \(N\) en el interior de la circunferencia en función de \(n\).
- Deduce que \(N\) coincide con las \(n\) primeras cifras de \(\pi\), salvo quizás la \(n\)-ésima, de la que se diferencia en una unidad como máximo.
Nota: pueden resultar útiles las desigualdades
$$0< \frac{1}{\arctan x} – \frac{1}{x} < x,$$
que se cumplen para \(x >0\).
Fe de erratas
Aunque ha pasado desapercibido para la mayoría de los lectores (incluyendo a quienes redactan este blog), el segundo punto no está enunciado correctamente. Lo que debería decir es que \(N\) coincide con el entero formado por las \(n\) primeras cifras de \(\pi\), del que se diferencia en una unidad como máximo. Así lo han entendido la mayoría de quienes han enviado una solución, y así se van a valorar las soluciones. Incluimos al final de la solución una discusión sobre este asunto. Dado que el comienzo de curso está dejando bastante que desear, pedimos aún más disculpas que la última vez a nuestros seguidores, sobre todo a quienes no enviaron una solución por no obtener lo que decía el segundo apartado o aquellos cuya solución se haya visto influida por el error en el enunciado.
Solución
Sea \(\alpha\) el ángulo \(\widehat{P_1P_2P_3}\).
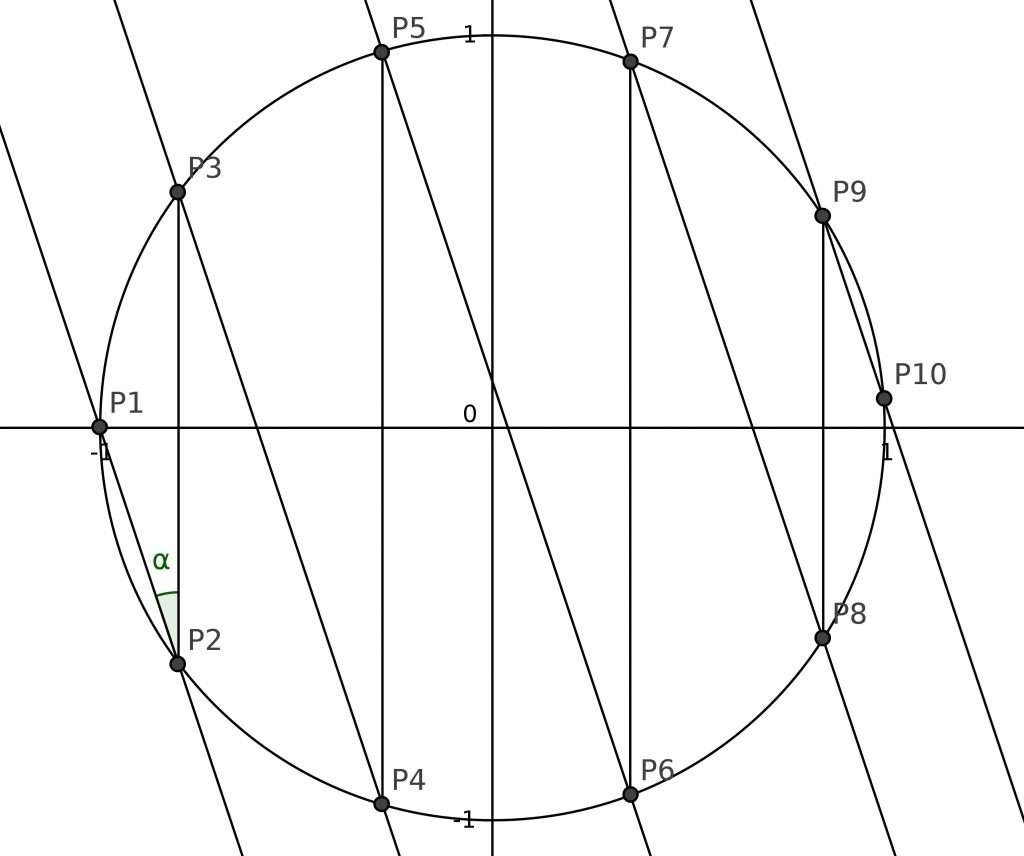
Como la pendiente de las rectas es \(-10^{n}\), tienen la dirección del vector \(\vec v = (1,-10^{n})\), y por tanto,
$$\tan \alpha = 10^{-n}, \qquad \alpha = \arctan (10^{-n}).$$
Por otra parte, por el teorema del ángulo central se tiene que \(\widehat{P_1OP_3} = 2\alpha\). Y como el arco \(P_1P_2\) es igual al arco \(P_1P_3\) ambos tienen longitud \(2\alpha\). De hecho, razonando igual con el resto de puntos, llegamos a que la circunferencia queda dividida en \(N\) arcos de amplitud \(\alpha\) y longitud \(2\alpha\) cada uno, más el arco \(P_NP_{N+1}\), que es más corto. Se tienen así las desigualdades
$$2\alpha N < 2\pi, \qquad 2\pi-2\alpha N < 2 \alpha,$$
de donde
$$ \frac{\pi}{\alpha} -1 < N < \frac{\pi}{\alpha}.$$
Por tanto, la expresión de \(N\) en función de \(n\) es
$$N=\left\lfloor \frac{\pi}{\alpha} \right\rfloor=\left\lfloor \frac{\pi}{\arctan (10^{-n})} \right\rfloor.$$
Nota: Estamos suponiendo que el arco \(P_NP_{N+1}\) es más corto que el resto. Cabe suponer qué ocurriría si, al realizar la construcción, \(P_{N+1}=(1,0)\), es decir, los puntos \(P_i\) delimitaran un polígono regular. En ese caso, \(\pi/\alpha\) sería entero y habría que sustituir la expresión anterior de \(N\) por \(\left\lceil\frac{\pi}{\alpha}\right\rceil-1\), que coincide con la anterior siempre y cuando \(P_{N+1}\neq(1,0)\). Sin embargo, lo anterior nunca puede suceder: \(\pi/\arctan x\) es un número racional solo si \(x=0,\pm1\). Para más detalles, ver este curioso artículo (Corolario 2).
Según las desigualdades que se dan en el enunciado del problema,
$$0<\frac{1}{\arctan(10^{-n})} – \frac{1}{10^{-n}} < 10^{-n}.$$
Teniendo en cuenta que \(\alpha = \arctan(10^{-n})\), se sigue que
$$10^n \pi < \frac{\pi}{\alpha}<10^n \pi + \frac{\pi}{10^n}.$$
Se tiene entonces que
$$\lfloor 10^n \pi \rfloor \leq N < 10^n \pi + \frac{\pi}{10^n}.$$
Por tanto, \(\lfloor 10^n \pi \rfloor\) (que contiene precisamente las \(n\) primeras cifras de \(\pi\), decimales o no) coincide con \(N\) o es una unidad menor.
Sobre el error en el enunciado: Que dos números enteros se diferencien en una unidad no significa, evidentemente, que todas sus cifras salvo la última coincidan. En nuestro caso, podría ocurrir que \(10^n \pi\) tuviera un nueve justo antes de la coma decimal y \(n-1\) nueves y al menos un siete detrás de la coma. En ese caso, puesto que \(10^{-n} \pi\) tiene siempre \(n-1\) ceros y un tres detrás de la coma, tendríamos que \(N=\left\lfloor 10^n \pi + \frac{\pi}{10^n}\right\rfloor=\lfloor 10^n \pi \rfloor+1\) se distinguiría de \(\lfloor 10^n \pi \rfloor\) en al menos las dos últimas cifras. No hay ninguna objeción para que esto ocurra; de hecho, si \(\pi\) es un número normal en base \(10\), seguro que sí sucede.
Nota: La idea del divertimento está tomada de https://interstices.info/le-nombre-pi-est-partout/ y completada con:
G. Galpering. Playing pool with \(\pi\) (the number \(\pi\) from a billiard point of view). Regular and chaotic dynamics. Vol 8, nº 4 (2003).

Dejar una contestacion