Pi y choque de masas

Este divertimento forma parte del concurso de 2024. Puedes encontrar las bases en este enlace.

Delantal

La presencia de \(\pi\) en las situaciones más imprevistas no deja de sorprender. Esta quincena vamos a celebrar el próximo día de \(\pi\) viendo su relación con el número de choques entre masas que siguen las leyes de la Física Clásica, y en este delantal explicamos el contexto que motiva el divertimento de más abajo.

Se consideran dos masas puntuales \(A\) y \(B\) e iguales. La masa \(A\) está inmóvil a cierta distancia de un muro plano \(L\) y \(B\) se lanza perpendicularmente al muro en la dirección de \(A\). Entonces \(A\) y \(B\) tienen un choque elástico perfecto, \(B\) se inmoviliza, \(A\) parte hacia el muro con la velocidad de \(B\), choca con \(L\), vuelve con la misma velocidad, choca con \(B\), se inmoviliza y \(B\) se aleja del muro. Se producen en total tres choques entre \(A\) y \(B\) y \(A\) y \(L\).

Si se repite el experimento poniendo una masa de \(B\) igual a \(10^2\) veces la de \(A\), se producen treinta y una colisiones. Y son \(314\) choques los que hay si la masa de \(B\) es \(10^{4}\) veces la de \(A\). ¿Cómo puede ser que aparezca \(\pi\) (o más bien sus cifras, poco a poco) en este experimento? En este vídeo se proporciona una justificación (no una prueba) de que el número de choques coincide con el número de segmentos que aparecen en el interior de la circunferencia en la siguiente construcción:

Es ahora cuando enlazamos con el enunciado del divertimento.

(La imagen de la portada es de Tang Yau Hoong en Flickr.)

Divertimento

Sea \(S\) la circunferencia de radio uno y origen el punto \((0,0)\), y sea \(P_1=(-1,0)\). Se considera un número entero positivo \(n\) y se traza la recta \(r_1\), que pasa por \(P_1\) y tiene pendiente \(m=-10^n\). La recta \(r_1\) corta a \(S\) en un punto \(P_2\). Sea ahora \(P_3\) el punto simétrico de \(P_2\) respecto del eje horizontal, y \(r_2\) la recta que pasa por \(P_3\) con pendiente \(m\).

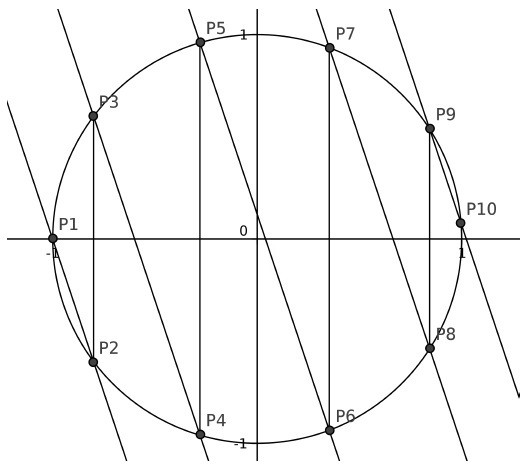
Esta construcción se puede iterar hasta obtener un punto \(P_{N+1}\) con dos coordenadas positivas y la primera mayor que la segunda, de modo que \(N\) coincide con el número de segmentos de la forma \(P_iP_{i+1}\) en el interior de la circunferencia. Se pide:

• Determina el número de segmentos \(N\) en el interior de la circunferencia en función de \(n\).
• Deduce que \(N\) coincide con las \(n\) primeras cifras de \(\pi\), salvo quizás la \(n\)-ésima, de la que se diferencia en una unidad como máximo.

Nota: pueden resultar útiles las desigualdades
$$0< \frac{1}{\arctan x} – \frac{1}{x} < x,$$
que se cumplen para \(x >0\).

Solución

Envía tus soluciones, hasta el viernes 15 de marzo, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el lunes 18 de marzo. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.