Solución: Un pentágono en un cubo

Publicamos la solución al divertimento Un pentágono en un cubo. En esta ocasión hemos recibido las respuestas acertadas de Renato Álvarez y Niurka Rodríguez, F. Damián Aranda Ballesteros, Juan Miguel Expósito, Marcos Jiménez y Manuel Zambrana, Antonio Medinilla Garófano y David Ramos Orozco, Don Pablo y Don Diedro, Rubén Ríos Mallqui y Cristóbal Sánchez-Rubio. 

Divertimento:

Este problema consta de dos cuestiones. La primera es probar que no es posible obtener un pentágono regular como sección de un cubo por un plano. La segunda es probar que sí es posible obtener como sección un pentágono con tres lados iguales y un eje de simetría. En este caso, si llamamos \(A\) al vértice que está sobre el eje de simetría y \(l\) a la longitud de cada uno de los tres lados iguales, se pide determinar los otros ángulos del pentágono y las longitudes de los otros dos lados en función de \(l\) y del ángulo del pentágono de vértice \(A\).

Solución:

En primer lugar, para que resulte un pentágono como sección de un cubo por un plano, dicho plano debe cortar a cinco caras del cubo entre las que hay cuatro que son paralelas dos a dos. Ya que el corte de un plano con dos planos paralelos da dos rectas paralelas, el pentágono resultante tiene obligatoriamente dos pares de lados paralelos y por tanto no puede ser regular.

Por otra parte, hay dos configuraciones para un pentágono con un eje de simetría y tres lados iguales.

 

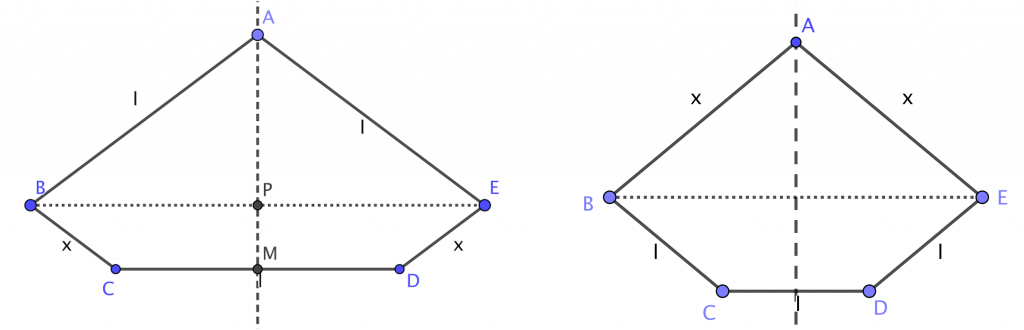
(1) En la figura de la izquierda, los lados iguales sean \(AB\), \(CD\) y \(EA\). Entonces se verifican las siguientes igualdades de ángulos (en grados)
$$ABP=90º- \frac{A}{2}, \qquad \qquad CBP=PEA=90º-\frac{A}{2},$$
de modo que los ángulos de vértices \(B\) y \(E\) valen cada uno
$$B=E=ABP+PBC=180º-A,$$
y los de vértices \(C\) y \(D\) valen
$$C=D=270º-\frac{A}{2}-B=90º+\frac{A}{2}.$$

En lo relativo a los lados, tenemos que \(AB=l\) y que \(CM=l/2\). Entonces, en el trapecio \(BPMC\) se tiene que

$$\displaystyle{\cos(CBP)=\frac{BP-CM}{BC},}$$
y del triángulo \(APB\) se deduce
$$BP=l \sin(A/2).$$
Por tanto
$$\displaystyle{\cos\left(90º-\frac{A}{2}\right)=\frac{l\sin(A/2)-l/2}{BC}=\sin\frac{A}{2}},$$
de donde
$$\displaystyle{BC=DE=l\frac{\sin(A/2)-1/2}{\sin(A/2)}}.$$

(2) En la figura de la derecha, los lados iguales son \(BC\), \(CD\) y \(DE\). Entonces, siguiendo un razonamiento similar al anterior,
$$\displaystyle{B=E=180º-A ,\qquad \qquad C=D=90º+\frac{A}{2}.}$$
Y, por otra parte,

$$\sin(A/2)=\frac{l/2+l \sin(A/2)}{AB},$$

de donde

$$AB=AE=l\frac{\sin(A/2)+1/2}{\sin(A/2)}.$$