No todos los problemas son iguales. Algunos son difíciles de entender, como la conjetura de Hodge, por cuya solución ofrecen un premio de \(1\,000\,000\) de dólares, pero que bien podrían dar \(100\,000\) por entenderlo. Otros son fáciles de entender pero casi imposibles de resolver, como la conjetura de Goldbach ¿es cada número par, suma de dos primos? Otros como el que presentamos hoy no es dificil de entender y está recién propuesto. Su dificultad está por ver, puede que sea fácil, puesto que no lo han intentado muchos matemáticos. Tiene el atractivo de haber sido propuesto por no matemáticos debido a sus posibles aplicaciones.
Plantear problemas es una tarea muy complicada. Cualquiera puede plantear problemas inaccesibles o triviales. Pero conseguir un problema fácil de entender, no trivial, pero que no parezca imposible de resolver es un arte difícil. El que presentamos hoy tiene todos los ingredientes para convertirlo en un gran problema. Por eso creo que sus autores merecen un reconocimiento. Para el que lo necesite (no es mi caso) tiene el atractivo de haber sido propuesto por no matemáticos debido a sus posibles aplicaciones.
El problema se refiere a una familia finita de conjuntos finitos. Antes de exponerlo necesitamos entender el principio de inclusión-exclusión.
El principio de inclusión-exclusión
El típico diagrama de Venn son tres conjuntos \(A\), \(B\) y \(C\) mostrando sus intersecciones
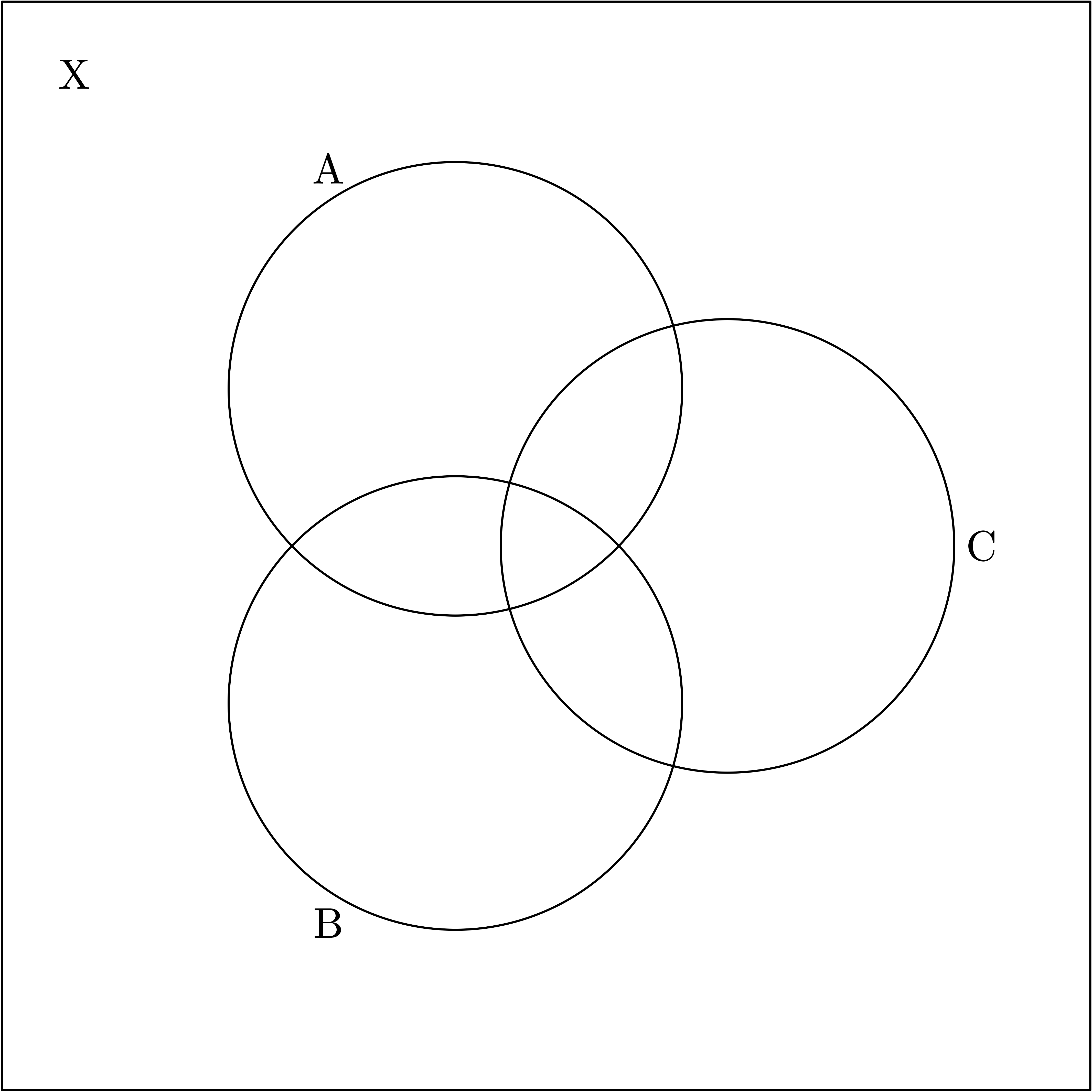
Podemos usarlo para contar los elementos del complemento de la unión \(X\smallsetminus (A\cup B\cup C)\). Si denotamos por \(|A|\) al cardinal de un conjunto finito, tendremos \begin{align*}
|X\smallsetminus &(A\cup B\cup C)|\\
&=|X|-|A|-|B|-|C|\\
&+|A\cap B|+|A\cap C|+|B\cap C|\\&-|A\cap B\cap C|.
\end{align*} Esto puede generalizarse al caso de un número finito de conjuntos \(A_1\), \(A_2\), . . . , \(A_N\). Para el caso general es conveniente introducir algo de notación. Sea \(I=\{1,2,\dots, N\}\) el conjunto de los subíndices y \(J\subset I\) un subconjunto, podemos definir la intersección $$A_J:=\bigcap_{j\in J} A_j,\qquad A_\emptyset:=X.$$ Cuando \(J=\emptyset\) la definición que damos es coherente/conveniente aunque un poco artificial. Entonces el principio se enuncia, usando \(|A|\) para denotar el cardinal de un conjunto $$\Bigl|X\smallsetminus\bigcup_{j=1}^N A_j\Bigr|=\sum_{J\subset I} (-1)^{|J|}|A_J|.$$
El principio de exclusión-inclusión es todavía un poco mas general. Aprovecho la ocasión para introducir una notación, debida a Iverson pero promovida por Donald Knuth, y que es muy conveniente. Si \(P\) es una proposición designamos por \([ P] \) el número \(1\) si \(P\) es verdadera y \(0\) si es falsa. De este modo \([ x\in A]\) es la función característica de \(A\). Esta notación es especialmente conveniente cuando aplicamos el teorema de Fubini. Por ejemplo convertimos la integral en un dominio plano \(D\) en la integral en un rectángulo introduciendo un factor \([ P(x,y)\le 0] \) en el integrando. Despejando \(x\) o \(y\) obtenemos los límites de integración. Por ejemplo $$[ x^2+y^2 \le1] = \Bigl[ -\sqrt{1-y^2}\le x\le \sqrt{1-y^2}\Bigr].$$
El principio de inclusión exclusión general se puede escribir entonces en la forma $$\Bigl[ x\in X\smallsetminus\bigcup_{j\in J} A_j\Bigr]=\sum_{J\subset I}(-1)^{|J|}[ x\in A_J].$$
Todavía debemos simplificar un poco la expresión anterior.
Supongamos ahora que \(X=\bigcup_{j=1}^N A_j\), en este caso el principio de exclusión-inclusión nos dice que $$0=\sum_{J\subset I}(-1)^{|J|}[ x\in A_J].$$ Teniendo en cuenta que uno de los términos de esta suma es \(A_\emptyset = X=\bigcup_{j=1}^N A_j\) obtenemos que $$\Bigl[ x\in \bigcup_{j=1}^N A_j\Bigr]=-\sum_{J\ne\emptyset}(-1)^{|J|}[ x\in A_J]\qquad \qquad(1).$$ La unión de los conjuntos \(A_j\) puede expresarse en términos de las intersecciones \(A_J\).
Pero en general hay intersecciones vacías, o también puede pasar que para \(J_1\ne J_2\) se tenga \(A_{J_1}=A_{J_2}\). Sean \(B_1\), . . . , \(B_M\) las intersecciones distintas entre las \(A_J\) con \(J\ne\emptyset\). Podemos reagrupar los términos en (1) y obtendremos $$\Bigl[ x\in \bigcup_{j=1}^N A_j\Bigr]=\sum_{m} a_m[ x\in B_m]\qquad \qquad(2),$$ donde los coeficientes \(a_m=-\sum_{A_J=B_m}(-1)^{|J|}\) son enteros positivos o negativos y no nulos (si \(a_m=0\) para algún \(m\) podemos eliminar ese término de la suma). La ecuación (2) es lo que llamaremos la expresión canónica del principio de inclusión-exclusión.
La Conjetura
Sean \(A_1\), . . . , \(A_N\) conjuntos finitos. \(B_1\), . . . , \(B_K\) las intersecciones de estos conjuntos que aparecen en la expresión canónica (2). La conjetura afirma que podemos construir la unión \(\bigcup_{n=1}^N A_n\) a partir de los conjuntos \(B_m\) usando las dos operaciones unión y complemento con la restricción de que las uniones sean disjuntas y los complementos solo se aplican a diferencias \(C_1\smallsetminus C_2\) que cumplan \(C_2\subset C_1\).
Es decir, existe una sucesión \(C_1\), . . . , \(C_R\) de conjuntos tales que \(C_R=\bigcup_{n=1}^N A_n\), y para cada \(C_r\) en la sucesión se cumpla una de las condiciones siguientes
- (a) \(C_r=B_m\) para cierto valor \(1\le m\le K\).
- (b) \(C_r=C_s\cup C_t\) con \(s\), \(t<r\) y \(C_s\cap C_t=\emptyset\).
- (c) \(C_r=C_s\smallsetminus C_t\) con \(s\), \(t<r\) y \(C_t\subset C_s\).
Consideremos un ejemplo. Damos los conjuntos iniciales \begin{gather*}A_1=\{3,4,5,7\},\quad A_2=\{1,2,7,10\}\\A_3=\{1,4,5,8\},\quad A_4=\{2,4,8,9\},\\ A_5=\{1,5,7,9\},\quad A_6=\{1,3,6,7\},\\ A_7=\{1,2,4,9\}\end{gather*} La expresión canónica es aquí complicada. Lo que haremos será dar la lista de conjuntos con coeficiente positivo en la forma \(B_1^r\), \(B_2^s\) donde los exponentes son los coeficientes \(a_m\) en la expresión canónica. El exponente \(1\) no lo escribiremos Los términos con coeficiente positivo son \(\{1\}^2\), \(\{4\}\), \(\{5\}\), \(\{7\}\), \(\{1,2,4,9\}\), \(\{1,2,7,10\}\), \(\{1,3,6,7\}\), \(\{1,4,5,8\}\), \(\{1,5,7,9\}\), \(\{2,4,8,9\}\), \(\{3,4,5,7\}\).
Los términos con coeficiente negativo son \(\{1,2\}^{-1}\), \(\{1,4\}^{-1}\),\(\{1,5\}^{-1}\), \(\{1,7\}^{-2}\), \(\{1,9\}^{-1}\), \(\{3,7\}^{-1}\), \(\{4,5\}^{-1}\), \(\{4,8\}^{-1}\), \(\{5,7\}^{-1}\), \(\{2,4,9\}^{-1}\).
Podemos reconstruir la unión usando estos conjuntos, por ejemplo como \begin{align*}&\{1,2,4,9\}\cup(\{2,4,8,9\}\smallsetminus\{2,4,9\})\cup\\&\cup\{5\}\cup(\{1,2,7,10\}\smallsetminus\{1,2\})\cup\\&\cup (\{1,3,6,7\}\smallsetminus\{1,7\})\end{align*}
En este caso, algunas intersecciones aparecen con coeficiente \(0\). Esos conjuntos los tenemos prohibidos para reconstruir \(X\). En este caso son pocos \(\emptyset\), \(\{2\}\) y \(\{9\}\).
Versiones de la conjetura
La suma de dos funciones características \([ x\in A]+[ x\in B]\) es una función característica \([ x\in A\cup B]\) si y solo si \(A\) y \(B\) son disjuntos. La diferencia \([ x\in A]-[ x\in B]\) es una función característica \([ x\in A\smallsetminus B]\) si y solo si \(B\subset A\). En el ejemplo anterior la conjetura nos decía que podíamos expresar la unión \(\{1,2,\dots, 10\}\) en la forma \begin{align*}&\{1,2,4,9\}\cup(\{2,4,8,9\}\smallsetminus\{2,4,9\})\cup\\&\cup\{5\}\cup(\{1,2,7,10\}\smallsetminus\{1,2\})\cup\\&\cup (\{1,3,6,7\}\smallsetminus\{1,7\})\end{align*} y esto es equivalente a \begin{align*}
[ x&\in \{1,2,\dots, 10\}]= [ x\in \{1,2,4,9\}]\\&+( [ x\in \{2,4,8,9\}]- [ x\in \{2,4,9\}])\\&\mskip-30mu+ [ x\in \{5\}]+( [ x\in \{1,2,7,10\}]- [ x\in \{1,2\}])\\&+( [ x\in \{1,3,6,7\}]- [ x\in \{1,7\}])\end{align*} dónde cada paréntesis (incluso los que no están puestos explícitamente correspondientes a las sumas) es una función que solo toma los valores \(0\) y \(1\), es decir, es una función característica.
En general la conjetura es equivalente a decir que existe una expresión de la función característica de la unión \(\bigcup A_n\) mediante sumas y diferencias de las funciones características de los conjuntos \(B_m\) que aparecen en la expresión canónica, con un orden en las operaciones expresado mediante paréntesis, y de manera que cada paréntesis sea una función característica.
Cuando en esta expresión simplificamos y agrupamos los términos iguales, obtenemos una expresión $$\Bigl[ x\in \bigcup_{j=1}^N A_j\Bigr]=\sum_{m=1}^K c_m[ x\in B_m],$$ donde ahora los \(c_m\) podrían ser \(=0\), si alguna de las intersecciones no se ha usado.
Conjetura fuerte. Podemos expresar la función característica de la unión de los \(A_m\), en la forma anterior, es decir, con los paréntesis siempre iguales a funciones características y de manera que \(|c_m|\le |b_m|\) y con los signos iguales, es decir, \(c_m b_m\ge0\).
También parece ser cierto, aunque menos interesante, que existe una expresión de este tipo con \(c_m=b_m\). Pero en realidad mientras mas pequeño sea \(\sum_{m=1}^K|c_m|\) mejor parece la expresión.
Los autores
Antoine Amarilli es profesor en la Escuela de ingeniería de Telecom en Paris, y aparte de sus interés en la Ciencia de los computadores está muy implicado en la crisis climática, también mantiene un blog. Mikaël Monet, es investigador en Ciencia de los computadores en el Inria en Lille y Dan Suciu es profesor de Ciencia de los computadores en la Universidad de Washington.



Ellos han formulado la cuestión planteada en sus trabajos que tienen que ver con bases de datos probabilistas, es decir en las que la respuesta a una pregunta no es unívoca sino que tiene ciertas probabilidades. El problema tiene que ver con la estrategia seguida para usar estas bases de datos y la existencia de ciertos circuitos para su implementación. Su mérito consiste en haber formulado una cuestión matemática precisa. También han confirmado la conjetura en los casos más simples, todos aquellos en que el conjunto total tiene \(\le 5\) elementos. El \(5\) puede parecer pequeño pero estamos considerando \(2^{2^5}\) posibilidades, que pueden reducirse si tenemos en cuenta isomorfismos. También han comprobado muchos casos con más elementos.
Yo mismo he hecho experimentos aleatorios, el ejemplo que he mostrado es uno de ellos. Dada la familia inicial de conjuntos \((A_n)\) he construido un programa que me da la correspondiente representación canónica. A partir de ella he buscado a mano la forma de expresar el conjunto total \(X\) usando los conjuntos permitidos, con el signo adecuado. Una especie de sudoku, del que a veces dudaba sobre si podría conseguir expresar \(X\). Pero siempre tuve la sorpresa de conseguirlo tras varios intentos.
Es posible probar que si usáramos todos las intersecciones \(A_J\) y no solo aquellas que tienen un coeficiente \(a_m\) no nulo, entonces sí que podemos obtener \(X\) usando solo uniones disjuntas y diferencias \(C_1\smallsetminus C_2\) con \(C_2\subset C_1\). Pero el problema práctico pide usar solo las intersecciones con coeficientes \(a_m\ne 0\).
Para saber más
El artículo del que hablamos hoy, contiene la formulación de la conjetura y los intentos sin éxito de probarla. Apareció en arXiv en enero de este año
El programa en Mathematica que he usado para obtener la expresión canónica es

El programa imprime Mobius que es una lista con elementos del tipo \(\{\{4,8\},-1\}\) conteniendo un conjunto \(B_m\) y su coeficiente \(a_m\).
Consideremos el caso de tres conjuntos
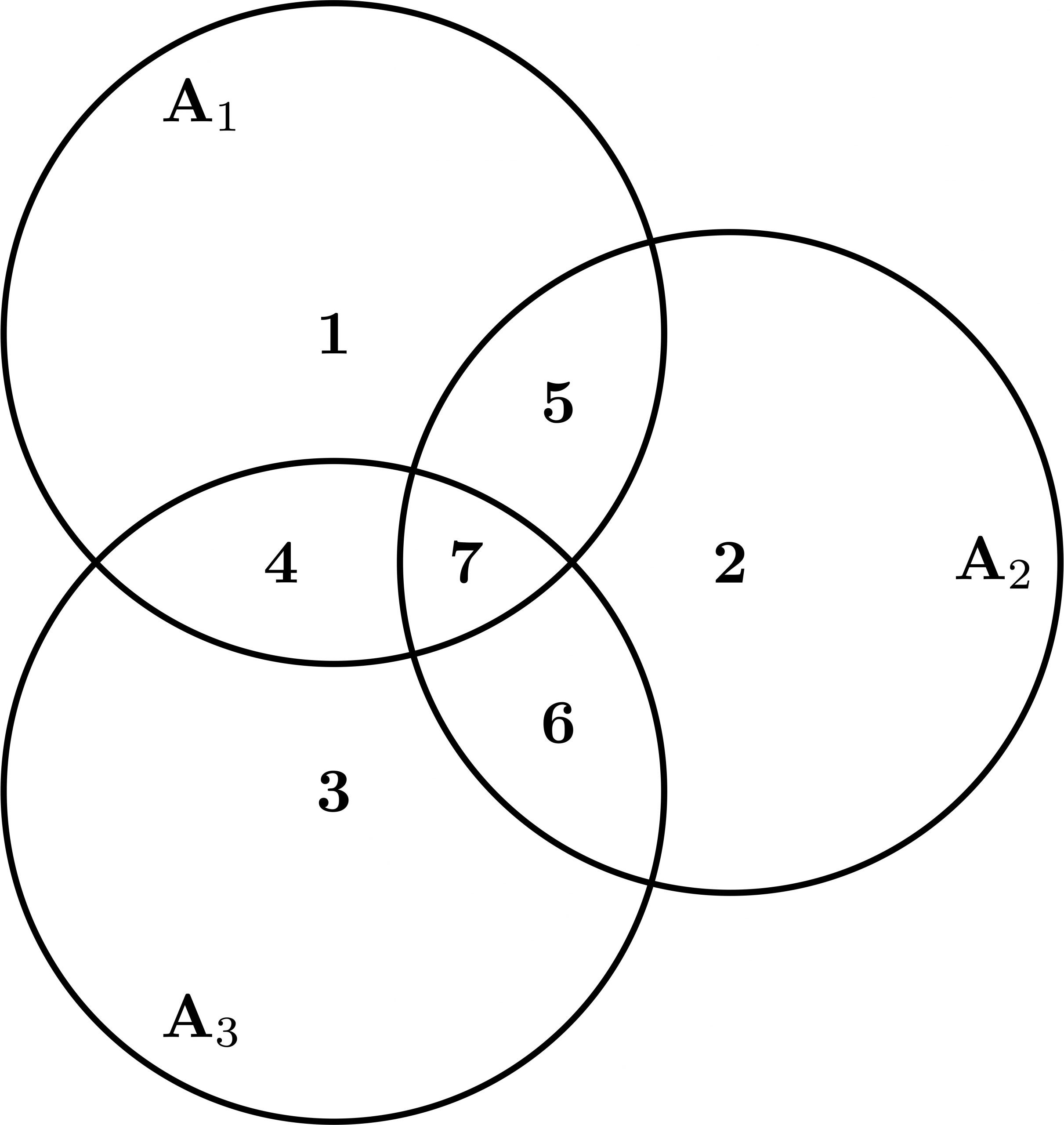
Las intersecciones son en este caso \(B_1=\{1,4,5,7\}\), \(B_2=\{2,5,6,7\}\), \(B_3=\{3,4,6,7\}\), \(B_4=\{5,7\}^{-1}\), \(B_5=\{4,7\}^{-1}\), \(B_6=\{6,7\}^{-1}\) y \(B_7=\{7\}\). Podemos obtener la unión, mediante las operaciones permitidas, usando todas las intersecciones y con el signo adecuado. Por ejemplo \begin{align*} &A_1\cup A_2\cup A_3\\&=B_1\cup(B_2\smallsetminus B_4)\cup\bigl[(B_3\smallsetminus B_5)\smallsetminus(B_6\smallsetminus B_7)\bigr]\end{align*} observar que \(B_7\) lleva como dos signos \(-\), así que cuenta como sumar una vez. Una descomposición como esta existe con \(N\) conjuntos con todas las intersecciones no vacías.
La representación anterior con \(N=3\) conjuntos es válida para el caso de 3 conjuntos en cualquier caso. Incluso si las intersecciones son vacías. Por ejemplo quitando el elemento \(4\) en todos los conjuntos anteriores tendremos \(B_5=A_1\cap A_3=A_1\cap A_2\cap A_3=B_7\). Por tanto esta intersección va con coeficiente \(=0\) y no puede usarse. Nosotros lo usamos dos veces en la representación anterior una vez con signo positivo y otra con el negativo. La solución aquí sería simple, basta sustituir en la representación anterior \(\bigl[(B_3\smallsetminus B_5)\smallsetminus(B_6\smallsetminus B_7)\bigr]\) por \(B_3\smallsetminus B_6\) que está permitida pues el \(4\) no está ahora contenido en \(B_1\). Pero todo esto en el caso general, de \(N\) conjuntos, es demasiado lioso.
La notación \([P]\) la uso con frecuencia desde que leí el artículo de Knuth
Donald Knuth, Two notes on notation, Amer. Math. Monthly, 99 (1992) 403-422. arXiv:math/9205211.
En muchos casos, como usando el teorema de Fubini, puede aclarar mucho las ideas.
La imagen destacada hoy es del usuario herraez.

Dejar una contestacion