Matemáticas para describir y vencer a la enfermedad de Alzheimer

Esta entrada tiene como principal objetivo convencer sobre la relevancia que tiene la investigación científica sobre la enfermedad de Alzheimer y, en particular, el análisis matemático y numérico de modelos que describen su evolución.

¿Qué es la enfermedad de Alzheimer?

El Alzheimer es una enfermedad neurodegenerativa progresiva que afecta a la memoria, a la capacidad de pensamiento y a la conducta. A medida que avanza, puede influir en la calidad de vida de quienes la padecen, muchas veces de manera trágica.

Se caracteriza por la acumulación de placas de proteína beta-amiloide en el cerebro, que dañan las células nerviosas y dificultan la transmisión de mensajes entre éstas. Con el tiempo, esto puede conducir de forma progresiva al olvido, confusión e irritabilidad, a la desorientación, a los cambios de humor, a los trastornos lingüísticos y, en etapas avanzadas, a la incapacidad para llevar a cabo actividades elementales.

Se piensa que en las personas con padre, madre o hermanos(as) con Alzheimer la probabilidad de desarrollo de la enfermedad es mayor. Aunque no se sabe muy bien por qué, se cree que los factores hereditarios (genéticos) y ambientales (o ambos) son importantes (el rango de herencia genética se estima entre el 50 y el 80 %, pero la causa de la enfermedad es en esencia desconocida).

Se estima que unas 800.000 personas padecen la enfermedad de Alzheimer en España, aproximadamente un 7 % de las personas de más de 65 años y un 20 % de las mayores de 85. Por otra parte, a nivel mundial, la Organización Mundial de la Salud (OMS) calcula una cifra aproximada de 60 millones de personas que viven con Alzheimer, con porcentajes aún mayores (un 8.1 % de mujeres y un 5.4 % de hombres mayores de 65 años). La zona de mayor incidencia en el mundo es América del Sur, seguida de los países con las rentas más altas de Asia (Japón, Corea del Sur y Singapur) y de Europa Occidental.

Para más información, véase por ejemplo [1, 2, 3].

El hallazgo

Alois Alzheimer (1864-1915) fue un psiquiatra y neurólogo alemán formado en las universidades de Tubinga, Berlín y Wurzburgo y posteriormente colaborador del neurólogo Franz Nissl (1860-1919). Trabajó principalmente en un hospital psiquiátrico en Francfurt.

En 1901, Alzheimer trató una paciente que le acabaría haciendo famoso: Auguste Deter. Su marido la había llevado al hospital, extrañado por su comportamiento. Se había vuelto incapaz de realizar las tareas más simples en el hogar, creía ver objetos donde no había nada, se irritaba con frecuencia, etc.

Hay constancia de la primera conversación que tuvo con la paciente. Respondía de manera incorrecta a preguntas muy simples (¿cuál es su apellido? ¿dónde vive?) y era incapaz de razonar.

Después de un prolongado seguimiento, el psiquiatra la diagnosticó con una dolencia que entonces era desconocida. La llamó «enfermedad del olvido» y publicó en 1907 los descubrimientos que hizo al examinar post mortem su cerebro.

Personas célebres con enfermedad de Alzheimer y sus mensajes

La lista de personas célebres que se han visto afectadas por esta enfermedad no es corta. Mencionemos algunas de ellas que, directa o indirectamente, han tenido impacto positivo en la sensibilización de la sociedad y la investigación médica:

\(\bullet\) Adolfo Suárez, primer Presidente de Gobierno de la España democrática. Fue diagnosticado con Alzheimer en la década de 1990.

\(\bullet\) Pasqual Maragall (Presidente de la Generalitat de Cataluña).

\(\bullet\) Terry Jones (Miembro de Monty Python). Fue diagnosticado con Alzheimer, en 2015. A pesar de la pérdida de sus habilidades lingüísticas, Jones continuó trabajando en proyectos creativos.

\(\bullet\) Rita Hayworth (actriz de Hollywood). Diagnosticada con Alzheimer en la década de 1980, en una época en que se sabía mucho menos sobre la enfermedad. Su hija, Yasmin Aga Khan, marcada por la evolución de su madre, ha dedicado enormes esfuerzos a concienciar al mundo entero sobre este gran problema y ha impulsado con gran energía la investigación científica en el ámbito.

\(\bullet\) Ronald Reagan (actor de Hollywood y ex-Presidente de los Estados Unidos). Anunció en 1994 que había sido diagnosticado con Alzheimer. Su actitud también ha contribuido a generar avances científicos en tiempos recientes.

En la actualidad, un buen número de científicos está dedicando sus esfuerzos a la investigación sobre las causas, la evolución y las posibilidades terapéuticas de la enfermedad de Alzheimer; véase por ejemplo [4, 5]. También se analiza con gran interés qué factores parecen incidir (positiva o negativamente) en su desarrollo. En este sentido, parece haberse descubierto recientemente que los consumos de viagra y de cannabis ralentizan la evolución, mientras que gestos como hurgarse la nariz pueden ser causa de aceleración; véase [6, 7, 8].

Para saber más (I): Qué pueden hacer las Matemáticas en este marco

Estamos todavía muy al principio. Sólo encontraremos 189 entradas en MathScinet referidas a trabajos que contengan «Alzheimer» en el título. Sin embargo, empieza a ser posible modelar la evolución de la enfermedad con herramientas matemáticas. Esto permitirá en el futuro mejorar nuestra comprensión de los mecanismos, simular casos concretos y quién sabe si determinar terapias efectivas.

Presentamos a continuación un modelo relativamente simple tomado de [9] que permite describir la evolución de la enfermedad.

Una hipótesis bien extendida afirma que la enfermedad de Alzheimer está motivada por la presencia y aumento de oligómeros tóxicos de \(\beta\)-amiloides en el cerebro. El \(\beta\)-amiloide es un compuesto de 36 a 43 aminoácidos que se sintetiza a partir de una proteína concreta. En química, un oligómero es una molécula formada por varias unidades estructurales similares (monómeros) enlazadas en cantidad moderada. Si se trata de dos unidades, el conjunto es un dímero, si son tres es un trímero, etc. Cuando el número de unidades es elevado la molécula resultante se suele denominar polímero.

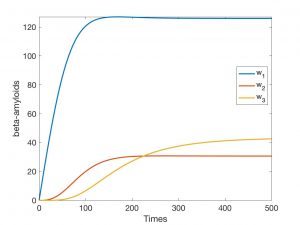
En este modelo, se supone que los monómeros de \(\beta\)-amiloide producidos por las células neuronales se van sucesivamente agregando en dímeros, trímeros, etc., hasta llegar a polímeros insolubles de larga longitud. Este fenómeno se modela fácilmente usando un sistema de EDOs donde las incógnitas son la concentración \(w_1\) de monómeros, las concentraciones \(w_2, \dots, w_{n-1}\) de oligómeros y la concentración \(w_n\) de polímero insoluble.

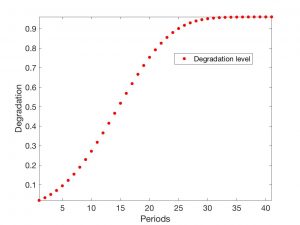
Aceptaremos que la producción de monómeros depende del nivel de degradación neuronal (una función \(a = a(t)\) que toma valores en \([0,1]\)) y que, a su vez, la agregación de oligómeros es tóxica y afecta a los valores que toma \(a\).

Para que el modelo sea mínimamente realista, fijaremos un abierto poliédrico \(\Omega\) ocupado por el cerebro y un mallado o triangulación del mismo \(\mathcal{T}_h\) y estudiaremos la evolución de los oligómeros y del nivel de degradación en cada elemento \(K \in \mathcal{T}_h\). Así, buscaremos funciones \(w_1, \dots, w_n\) y \(a\) en el espacio
$$
A_h = \{ v \in L^2(\Omega) : v|_K \in \mathbb{P}_0(K) \ \ \forall K \in \mathcal{T}_h \} .
$$

Para cada \(K\), denotaremos \(w_{i,K}\) y \(a_K\) las correspondientes restricciones e impondremos el siguiente sistema acoplado:

Primer bloque – Evolución de los \(\beta\)-amiloides:
$$
\frac{dw_{1,K}}{dt} = -k w_{1,K} \sum_{j \leq n-1} w_{j,K} – k^*w_{1,K} w_{n,K} + \Lambda_K(t) – M_1 w_{1,K} ,
$$
$$
\frac{dw_{i,K}}{dt} = -\frac{k}{2} \sum_{j+\ell = i} w_{j,K} w_{\ell,K} – kw_{i,K} \sum_{j \leq n-1} w_{j,K} – k^*w_{i,K} w_{n,K} – M_i w_{i,K}
$$
para \(i = 2, \dots, n-1\) y
$$
\frac{dw_{n,K}}{dt} = -\frac{k}{2} \sum_{(j,\ell) \in S} w_{j,K} w_{\ell,K} – M_n w_{n,K} ,
$$

donde \(S = \{ (j,\ell) : 1 \leq j,\ell < n, \ \ j+\ell \geq n \}\). Se interpreta que \(\Lambda_K = \Lambda_K(t)\), las \(M_i\) y las constantes \(k\) y \(k^*\) determinan respectivamente la producción de monómeros, la mortailidad y los ritmos de agregación.

Segundo bloque – Evolución del nivel de degradación (y de la enfermedad):
$$
a_K(t) = a_K(mT) + \theta \left( D_K(mT) – D^* \right)_+
\ + \ \sigma \!\!\!\!\sum_{K’ \in \mathcal{E}(K)} \left( a_{K’}(mT) – a_K(mT) \right)_+
$$
en \((mT,(m+1)T]\), donde
$$
D_K := \sum_{2\leq i \leq n-2} \gamma_i w_{i,K}, \quad \mathcal{E}(K) = \{ K’ \in \mathcal{T}_h : \text{int }(K’ \cap K) \not= \emptyset \} ,
$$

las \(\gamma_i\) y \(D^*\) son constantes positivas, \(T > 0\) es un período razonable de estabilidad degenerativa y \(m = 0, 1, 2, \dots\). A continuación, tomamos
$$
\Lambda_K(t) = A(1 – a_K(t))(1 + \beta a_K(t)) \ \text{ en } \ (mT,(m+1)T] ,
$$
donde \(A\) y \(\beta\) son constantes positivas.

Vemos por tanto que, en este modelo, la evolución de las concentraciones de oligómeros es mucho más rápida que la de las funciones \(a_K\) (que, por otra parte, son constantes a trozos en tiempo). Esto es coherente con la realidad. También vemos que los cambios de \(a_K\) de \(mT\) a \((m+1)T\) se deben a efectos locales (cuando \(D_K(mT) > D^*\)) y a efectos globales (cuando en el entorno de \(K\) hay valores de \(a_{K’}(mT)\) que son mayores).

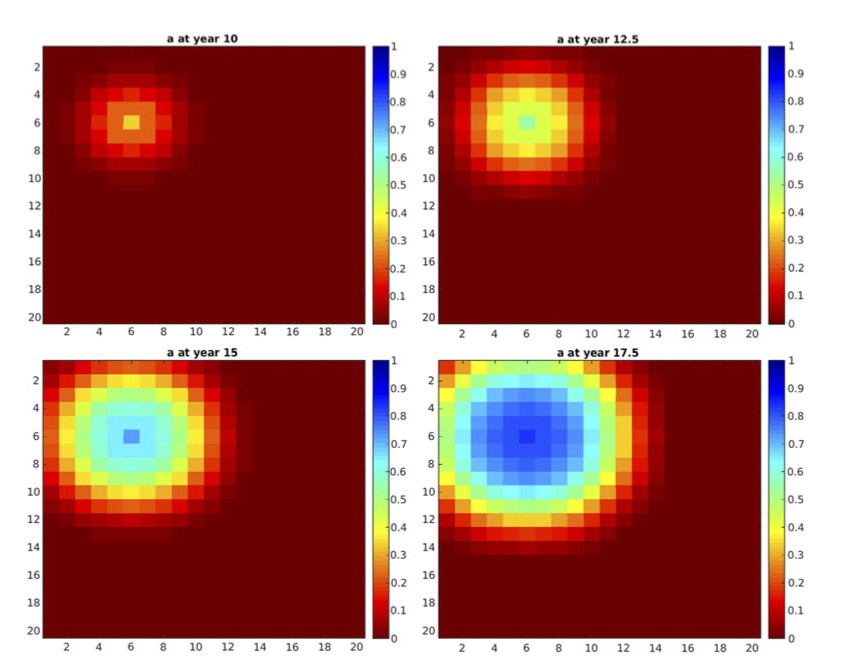
Fijados \(\Omega\), el mallado \(\mathcal{T}_h\) y datos iniciales en \(A_h\) para las \(w_i\) y para \(a\), existe una única solución del sistema precedente.

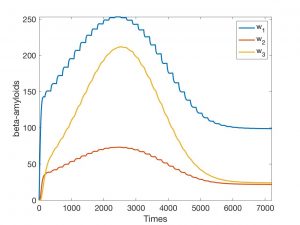
Una experiencia numérica para un modelo 2D simplificado definido con precisión en [9] está descrita en las Fig. 3-6. Se ha supuesto que el dominio de trabajo es el cuadrado \((0,20) \times (0,20)\) y que \(\mathcal{T_h}\) es un mallado regular constituido por \(400\) cuadrados de lado unidad. Hemos simplificado el sistema, tomando \(n= 2\) y suponiendo por tanto que sólo un oligómero es tóxico. En la Fig. 3 aparece la evolución de las \(w_{i,K}\) en un \(K\) arbitrario aislado cuando el nivel de degradación es \(0\). En la Fig. 4 queda reflejada esta evolución en un \(K\) aislado (sin interacción con los \(K’\) del entorno) cuando el nivel inicial de degradación es pequeño pero positivo. La evolución de \(a_K\) ha sido visualizada en la Fig. 5. Finalmente, una vez resuelto el sistema completo con un dato inicial para \(a\) que es sólo positivo y pequeño en un elemento, vemos en la Fig. 6 cómo evolucionan los valores a medida que avanza el tiempo.

Otros modelos más elaborados pueden encontrarse en [10, 11]. Para una recopilación de resultados conocidos, véase [12].

Para saber más (II): Algunas referencias

1. https://www.alz.org/media/documents/alzheimers-facts-and-figures.pdf.
2. T.C. Saido, Alzheimer’s Disease Research Guide. Animal Models for Understanding Mechanisms and Medications, Elsevier, 2024.
3. B. Prajapati, D.K. Chellappan, P. Kendre. Alzheimer’s Disease and Advanced Drug Delivery Strategie, Elsevier, 2023.
4. Y. Zhang and others. Amyloid ?-based therapy for Alzheimer?s disease: challenges, successes and future, Signal Transduction and Targeted Therapy (2023) 8 : 248.
5. U. Sehar and others. Amyloid Beta in Aging and Alzheimer?s Disease. Int. J. Mol. Sci. 2022, 23, 12924.
6. M. Adesuyan and others, Phosphodiesterase Type 5 Inhibitors in Men With Erectile Dysfunction and the Risk of Alzheimer Disease: A Cohort Study. Neurology 2024; 102:e209131.
7. A. Currais and others. Amyloid proteotoxicity initiates an inflammatory response blocked by cannabinoids. Aging and Mechanisms of Disease (2016) 2, 16012.
8. X. Zhou. Neuroinflammation in Alzheimer?s Disease: A Potential Role of Nose-Picking in Pathogen Entry via the Olfactory System. Biomolecules 2023,13,1568.
9. M. Berstch and others. The amyloid cascade hypothesis and Alzheimer?s disease: A mathematical model. Euro. J. of Applied Mathematics (2021), vol. 32, pp. 749-768.
10. M. Berstch and others. The role of A-beta and tau proteins in Alzheimer’s disease: a mathematical model on graphs. J. Math. Biol. 87 (2023), no. 3, Paper No. 49.
11. W. Hao, A. Friedman. Mathematical model on Alzheimer?s disease. BMC Systems Biology (2016) 10:108
12. F. Carbonell, Y. Iturria-Medina, A.C. Evans. Mathematical Modeling of Protein Misfolding Mechanisms in Neurological Diseases: A Historical Overview. Front. Neurol., 02 February 2018 Sec. Neurodegeneration, Volume 9 – 2018.