Publicamos la solución al divertimento de las dos torres. Muchas gracias a Renato Álvarez Rodríguez y Niurka Rodríguez Quintero, F. Damián Aranda Ballesteros, Marcos Jiménez y Manuel Zambrana, Antonio Medinilla Garófano y David Ramos Orozco, Don Pablo y Don Diedro, José Luis Ramírez Fabra, Ruben Ríos Mallqui y Cristóbal Sánchez-Rubio por las soluciones que nos han enviado. Se ha recibido una solución parcialmente correcta de Jesús Reyes Toro y Víctor Sánchez Sánchez.
Divertimento
La Torre Sevilla y la Giralda, que se encuentran a una distancia de aproximadamente 1670 metros, miden respectivamente 180,5 y 94,7 metros. Pero hay ciertos puntos, más próximos a la Giralda que a la Torre Sevilla, desde los cuales ambas torres aparentan tener la misma altura, es decir, el ángulo de elevación de su punto más alto, medido desde el suelo, es el mismo. ¿Cuáles son esos lugares?
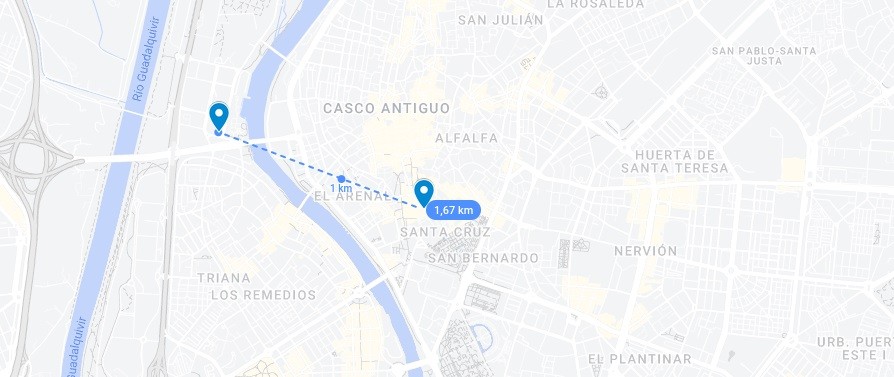
Nota: Suponemos que ambas construcciones se encuentran en una superficie plana.
Solución
Supongamos que estamos a una distancia \(d_1\) de la Torre Pelli, de altura \(h_1\), y a una distancia \(d_2\) de la Giralda, de altura \(h_2\), en un punto desde el que ambas tienen la misma altura aparente, y por tanto tienen el mismo ángulo de elevación \(\alpha\). En tal caso,
$$\frac{h_1}{d_1}=\tan \alpha = \frac{h_2}{d_2},$$
y así el cociente entre las distancias a ambas torres es constante,
$$\frac{d_1}{d_2}=\frac{h_1}{h_2}=c.$$
El lugar geométrico de los puntos del plano para los que el cociente de las distancias a otros dos puntos fijos es constante es una circunferencia, que se conoce como circunferencia de Apolonio. Supongamos que la Torre Pelli es el punto \(A=(0,0)\) del plano y la Giralda, el punto \(B=(0,b)\). Los puntos \(P=(x,y)\) que se buscan cumplen que
$$d(P,A)=d_1, \quad d(P,B)=d_2, \quad \frac{d_1}{d_2}=c.$$
Por tanto,
$$\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+(y-b)^2}}=\frac{d_1}{d_2}=c,$$
y de aquí,
$$x^2+y^2=c^2(x^2+(y-b)^2).$$
Desarrollando la identidad anterior, llegamos a que
$$\frac{c^2 b^2}{c^2-1} =x^2+y^2-2\frac{c^2b}{c^2-1}y.$$
Ahora, completando cuadrados se obtiene la ecuación de la circunferencia:
$$\left(\frac{c^2 b}{c^2-1}\right)^2 – \frac{c^2 b^2}{c^2-1} =x^2 + \left( y- \frac{c^2 b}{c^2-1}\right)^2.$$
Su centro y su radio son, respectivamente,
$$O=\left(0,\frac{c^2 b}{c^2-1}\right), \quad R=\sqrt{\left(\frac{c^2 b}{c^2-1}\right)^2 – \frac{c^2 b^2}{c^2-1}}$$
Observamos que el centro de la circunferencia que se obtiene está alineado con ambas torres. Teniendo en cuenta que \(b=1670\) y que \(c=180,\!5/94,\!7\), se tiene aproximadamente que
$$O=(0,2304,\!3), \qquad R=1209$$
Es decir, el centro de la circunferencia (alineado con la Torre Sevilla y con la Giralda, a 2304,3 metros de la primera) se encuentra en la esquina del edificio de la Diputación de Sevilla que da a la confluencia de las calles Rastro y General Ríos.
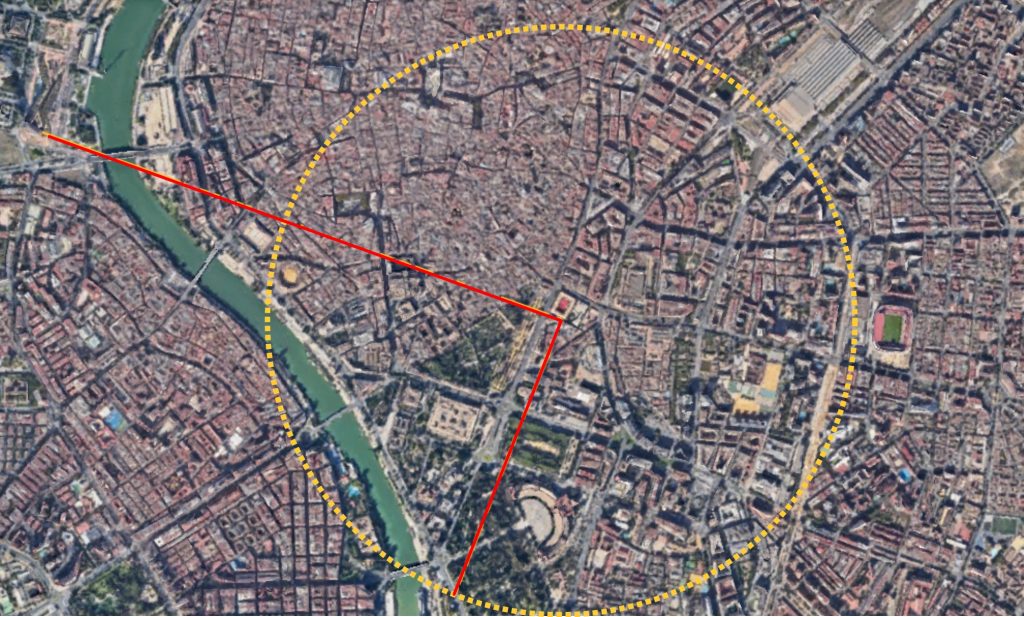
La Calle Betis, desde donde se grabó el vídeo, parece un buen lugar desde el que comprobar si ambas torres aparentan tener, efectivamente, la misma altura. Uno de nuestros lectores, Renato Álvarez Rodríguez, nos sugiere realizar una excursión al centro de Sevilla para encontrar otros lugares apropiados. Nos parece un trabajo muy interesante, y animamos a nuestros lectores a recorrer los nueve kilómetros y pico de la circunferencia trazada, evitando, eso sí, los tramos ocupados por edificios, y cruzando con cuidado el río y calles y avenidas transitadas.

Dejar una contestacion