En esta entrada y la que sigue, hablaremos de los orígenes, el desarrollo reciente, las aplicaciones y el futuro previsible de la teoría de control. En varias entradas anteriores hemos podido encontrar múltiples aplicaciones: vehículos autónomos, control de las epidemias, control de la polución y de enfermedades como la diabetes, etc. Podremos observar que se trata de una rica parcela de las Matemáticas íntimamente conectada con las Ciencias y la Ingeniería que ha tenido una enorme importancia en la evolución del mundo. Descubriremos también que conduce a un gran número de cuestiones abiertas de máximo interés teórico.
Qué es el control de sistemas
El término control posee, entre otros, dos significados: comprobación (o chequeo) y gobierno (o liderazgo). En el contexto de la teoría matemática de control, debemos referirnos al segundo de ellos.
A lo largo de la Historia, ha sido un deseo permanente conseguir gobernar el comportamiento o «controlar» los sistemas que nos rodean, con la finalidad de mejorar nuestras condiciones de vida. Esto se ha materializado en el diseño y construcción de herramientas y máquinas de todo tipo y, más recientemente, en la determinación de estrategias de actuación, siempre con el objetivo de optimizar el rendimiento.
El control en la antigüedad
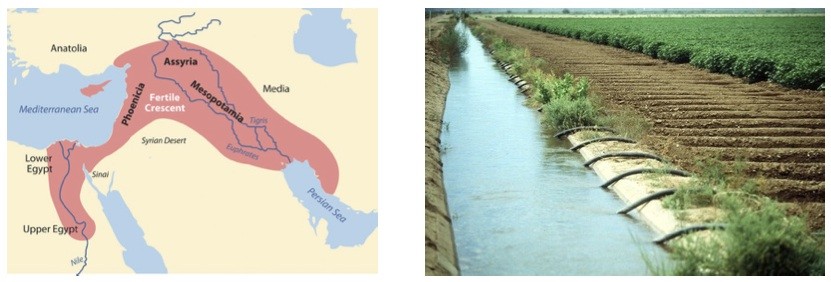
Tal vez el primer ejemplo de control se encuentra en el sistema de regadíos desarrollado en Mesopotamia, hacia el año 6.000 A.C. El ingenioso entrelazado de canales y compuertas permitía mantener el nivel de agua necesario para dar vida a la región a pesar de las duras condiciones geográficas y climatológicas.

Un caudal irregular e incluso «caprichoso» podía ser controlado de este modo, produciendo enormes beneficios.
Este logro está conectado con otra gran invención de la antigüedad: los acueductos romanos, construidos entre los siglos II A.C. y IV D.C. En este caso, conductos de largas dimensiones adaptados a las condiciones geográficas circundantes hicieron posible transportar y suministrar agua con eficacia desde fuentes lejanas hasta centros urbanos.
Es fácil convencerse de la gran dificultad que tiene conseguir el funcionamiento correcto de un acueducto: hay que conseguir que el caudal llegue a su destino con el ritmo más constante posible, de la manera más independiente posible de la aportación y de las condiciones meteorológicas. Esto exige incorporar al diseño elementos de diversa índole que produzcan efectos estabilizadores: desniveles y ensanchamientos del conducto, cámaras de aire, etc.

La máquina de vapor
Se acepta que la máquina de vapor constituyó en su día el punto de arranque de la ingeniería industrial basada en el control de sistemas.
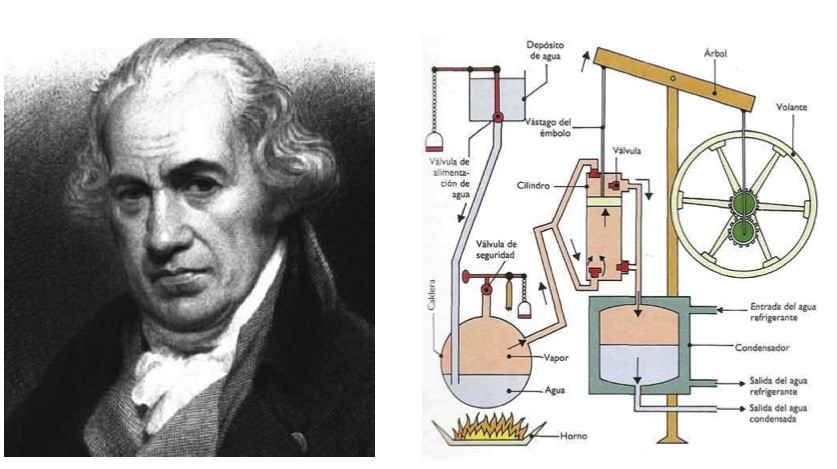
El funcionamiento de las primeras máquinas de vapor se basaba en el siguiente ciclo de trabajo: (1) Se genera vapor de agua por calentamiento en una caldera cerrada, lo que produce movimiento de rotación de una plataforma, (2) Al girar la plataforma, quedan abiertas válvulas de escape que disminuyen la presión del vapor y, en consecuencia, producen una reducción de la velocidad de rotación. (3) Esta reducción tiene como efecto que las válvulas se cierren, con lo que la presión y la velocidad de giro vuelven a aumentar, etc.
La idea crucial que había detrás era, por tanto, poner en práctica un mecanismo de autoregulación que permitía controlar la velocidad a la que giraba la plataforma. Fue desarrollada y perfeccionada por varios inventores de los siglos XVII y XVIII: Denis Papin, Thomas Savery, Thomas Newcomen y, sobre todo, el ingeniero escocés James Watt.
La máquina de vapor fue un elemento de desarrollo fundamental durante la Revolución Industrial. Permitió mover máquinas y aparatos diversos: bombas, locomotoras, motores marinos, etc.
La formulación matemática

La primera formulación matemática de un problema de control se debe a James C. Maxwell.
Apareció en un trabajo publicado en 1868, donde se introducen los conceptos de «moderador» y «gobernador». En pocas palabras, un moderador es un artilugio que corrige la velocidad de un dispositivo tratando de hacer mínima su desviación respecto de una velocidad deseada. Por su parte, un gobernador es un mecanismo análogo cuya acción está destinada a minimizar la integral en tiempo de la desviación precedente.
En ambos casos, se dice que el proceso seguido para controlar el comportamiento del dispositivo está regido por una ley de «feedback» (o retroalimentación): reposa sobre la observación del comportamiento de éste (la clave está en saber cuánto nos estamos desviando en cada instante de la situación deseada).
Los grandes nombres de la teoría de control moderna aparecieron en el siglo XX:
Rudolph Kalman, Lev S. Pontryagin y Richard Bellman. Estudiaron sistemas donde uno de los datos, denominado «control», debe ser elegido para que la solución, denominada «estado», cumpla propiedades deseadas.

Entre otros logros, Kalman, introdujo el concepto de controlabilidad. Dedujo condiciones necesarias y suficientes para que un sistema diferencial ordinario fuera controlable. Esto permitió conducir sistemas con origen muy diverso de situaciones iniciales desfavorables a situaciones deseadas con precisión. Por ejemplo, un hábitat donde conviven poblaciones que interactúan en cascada puede ser conducido, con alimentación adecuada administrada durante un período de tiempo suficientemente largo a un estado de equilibrio.
Por su parte, Pontryagin formuló el principio que lleva su nombre: una condición necesaria (y bajo ciertas condiciones suficiente) para que un control sea «óptimo», esto es, haga máxima una función de beneficio en una familia de controles admisibles. Bellman formuló y probó un resultado equivalente, denominado principio de la programación dinámica.
Como veremos en una segunda parte de esta entrada, la importancia de estos resultados es enorme en la actualidad. Por ejemplo, cuando se describe la evolución de un tumor en presencia de una terapia radiológica, aparecen de forma natural problemas de control óptimo cuya solución puede ayudar a comprender la eficiencia de los distintos tratamientos posibles.
Para saber más
- https://www.youtube.com/watch?v=5RP2KfewiJA
- https://www.youtube.com/watch?v=RqScpCHA08U
- Stuart Bennett, «A History of Control Engineering, 1930-1955», Peter Peregrinus Ltd., London, 1993.
- Enrique Fernández-Cara, Enrique Zuazua, «Control Theory: History, Mathematical Achievements and Perspectives», Bol. SeMA no. 26 (2003), 79-140.
- James C. Maxwell, «On Governors», Proceedings of the Royal Society, no. 100 (1868), en «The Scientific Papers of James Clerk Maxwell», vol. II, pp. 105-120.

Dejar una contestacion