En esta entrada hablaremos de nuevo de la teoría de control. Nos centraremos principalmente en las aplicaciones donde juega un papel importante hoy día.
Cómo y para qué se están controlando algunos de los sistemas que nos rodean
Para conseguir una temperatura constante en una habitación, es preciso que un mecanismo de «feedback» esté actuando de manera permanente.

Un mecanismo similar es también necesario para que la señal aérea que llega a un receptor de TV tenga la intensidad adecuada, o el funcionamiento de un teléfono móvil sea el apropiado, o el sistema de frenado de un automóvil funcione correctamente, o el sistema de localización de una embarcación proporcione resultados con precisión y rapidez.
Existen muchas más situaciones donde los beneficios que producen las técnicas de control son claros. Así, podemos mencionar los sistemas de conducción automática, los sistemas de grabación (que consiguen mantener un nivel de sonido consistente), los sistemas de guiado de robots domésticos, etc.
Prácticamente en todos los casos, los fenómenos considerados se pueden modelar mediante un sistema de ecuaciones diferenciales (más o menos complicadas) en el que algunos datos van siendo fijados de acuerdo con la solución que producen. Por ejemplo, en el caso de la conducción automática de un vehículo, el sistema toma la forma
$$
\left\{
\begin{array}{l}\displaystyle
y_t = F(y, u_1, u_2), \quad t \in (0,T),
\\ \displaystyle
y(0) = y_0 ,
\end{array}
\right.
$$
donde \(u_1 = u_1(t)\) y \(u_2 = u_2(t)\) determinan la dirección y la velocidad del vehículo, la incógnita \(y = y(t)\) sirve para identificar su posición y el par \((u_1(t),u_2(t))\) se elige en cada instante de tiempo \(t\) de manera que \(y(T)\) coincida con un valor dado y la cantidad
$$
\max_{[0,T]} |y(t) – \overline{y}(t)|,
$$
donde \(\overline{y} = \overline{y}(t)\) es una trayectoria deseada, sea lo menor posible.
La (enorme) familia de aplicaciones
Tradicionalmente, la teoría de control ha servido para sustentar muchas aplicaciones propias de la Ingeniería.
Desde hace tiempo, se ha usado en el diseño y optimización de procesos industriales, control de calidad,

automatización de la fabricación de productos y determinación de un transporte eficiente y seguro. También, ha ayudado en gran medida en el desarrollo de algoritmos que hacen posible a un robot el desplazamiento, el desempeño de tareas de manera autónoma y la toma de decisiones. Incluso está detrás de los mecanismos de coordinación de robots múltiples con objetivos comunes.
Pero el ámbito de aplicaciones es mucho más extenso. En efecto, los resultados a los que conduce son actualmente utilizados con éxito entre otros en problemas con origen en
- Economía y finanzas: con frecuencia, la teoría permite modelar e incluso predecir dinámicas económicas que pueden ayudar al análisis y a la formulación de políticas adecuadas. A nivel particular, permite optimizar estrategias de inversión y minimizar riesgos asociados, véase [1].
- Climatología y Ciencias Medioambientales: el uso de recursos naturales, la contaminación, la sostenibilidad del planeta, el impacto del cambio climático, etc. son elementos a los que tiene perfecto sentido aplicar las técnicas.
- Biología y Medicina: es posible de nuevo modelar y optimizar sistemas propios de la dinámica de poblaciones, regular procesos biológicos y determinar estrategias terapéuticas óptimas en el tratamiento de múltiples enfermedades. Para detalles, véase por ejemplo [2].
- Sociología: los fenómenos de comportamiento e interacción social constituyen desde hace algún tiempo una importante fuente de problemas a los que la teoría de control puede dar respuesta. A este respecto, véase [3].
En tiempos recientes, se ha profundizado con intensidad en la conexión de la teoría de control con elementos del aprendizaje automático (machine y deep learning). En particular, se observa que las técnicas de control permiten llevar a cabo un «aprendizaje reforzado», donde los agentes aprenden a tomar decisiones basadas en un proceso de feedback relativo al entorno; véase [4]. Este tema merece por sí solo una o varias entradas que posiblemente verán la luz próximamente.
Para saber más (I): Ideas fundamentales
El primer elemento de un problema de control es el sistema de estado. Con gran frecuencia, se trata de un problema de evolución
$$
\left\{
\begin{array}{l}\displaystyle
y_t = A(y,v), \quad t \in (0,T),
\\ \displaystyle
y(0) = y_0 ,
\end{array}
\right.
\qquad (1)
$$
donde \(y = y(t)\) es la solución (el estado) y \(v = v(t)\) es un dato (el control). Se supone que el estado es una función definida en \([0,T]\) con valores en \(H\) (un espacio de Hilbert) y el control pertenece a \(U\) (otro espacio de Hilbert); también, suponemos que \(A\) es una aplicación dada (lineal o no) e \(y_0 \in H\) es un dato inicial fijo.
En la práctica, esta formulación engloba una gran cantidad de situaciones de dificultad variable. Así, \(H\) y \(U\) pueden ser o no finito-dimensionales, \(A\) puede ser una aplicación lineal, un complicado operador diferencial o integro-diferencial, etc.
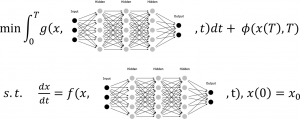
En los problemas de control óptimo, se fijan además una familia \(U_{ad}\) de controles admisibles (un subconjunto de \(U\)) y una función de coste \(J : U_{ad} \to {\bf R}\). Se supone que para cada \(v \in U_{ad}\) existe una única solución \(y_v \in L^2(0,T;H)\) de \((1)\) y que \(J\) es de la forma
$$
J(v) = J_0(v,y_v) \ \text{ con } \ J_0 : U_{ad} \times L^2(0,T;H) \to {\bf R} .
$$
El problema consiste en determinar \(\hat{v}\) tal que
$$
J(\hat{v}) \leq J(v) \quad \forall v \in U_{ad} \ \text{ con } \ \hat{v} \in U_{ad} .
$$
Caso de existir, se dice que \(\hat{v}\) es un control óptimo.
Un caso particular sencillo corresponde al sistema diferencial ordinario
$$
\left\{
\begin{array}{l}\displaystyle
y_t = a(y) + bv, \quad t \in (0,T),
\\ \displaystyle
y(0) = y_0 ,
\end{array}
\right.
\qquad (2)
$$
donde \(H = {\bf R}\), \(a \in C^1({\bf R})\) y \(b \in {\bf R}\), con
$$
U = L^2(0,T), \quad U_{ad} = \{ v \in L^2(0,T) : v \geq 0 \ \text{ c.p.d.} \}
$$
y
$$
J(v) = \dfrac{\alpha}{2} \int_0^T |y_v(t) – \overline{y}|^2 \,dt
+ \dfrac{\beta}{2} \int_0^T |v(t)|^2 \,dt ,
\qquad (3)
$$
donde \(\overline{y} \in {\bf R}\) y \(\alpha, \beta > 0\).
Las cuestiones más interesantes son las siguientes:
- ¿Existe control óptimo? ¿Es único?
- ¿Cómo podemos caracterizar los controles óptimos? Es decir, ¿es posible deducir un sistema de optimalidad para \(v\), el estado asociado \(y_v\) y posiblemente alguna función adicional necesariamente verificado por estas variables cuando \(v\) es un control óptimo?
- ¿Cómo calcular el o los controles óptimos caso de que existan?
En el caso particular del problema \((2)\)-\((3)\), el sistema de optimalidad es fácil de obtener. Se trata del siguiente:
$$
\left\{
\begin{array}{l}\displaystyle
y_t = a(y) + bv, \quad t \in (0,T),
\\ \displaystyle
y(0) = y_0 ,
\\ \\ \displaystyle
-\phi_t = a'(y)\phi + \alpha (y – \overline{y}), \quad t \in (0,T),
\\ \displaystyle
\phi(T) = 0 ,
\\ \\ \displaystyle
v = \left(-\dfrac{\alpha}{\beta} \phi \right)_+ .
\end{array}
\right.
$$
Se observa que, a partir del mismo, es factible deducir una regla de feedback que permite determinar controles óptimos a partir de los valores que toman los estados asociados:
$$v \to y \to \phi \to v,$$
donde la notación es auto-explicativa; véase [5].
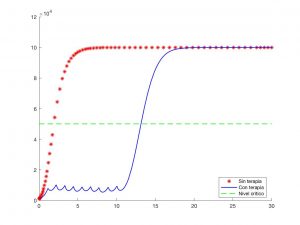
Una manera distinta de controlar un sistema reposa sobre la idea de hallar controles que «conducen» la solución a un estado deseado. Por ejemplo, el problema de controlabilidad nula (o exacta a cero) para \((1)\) consiste en hallar un control \(\tilde{v} \in U_{ad}\) tal que la solución asociada \(\tilde{y}\) verifica
$$
\tilde{y}(T) = 0.
$$
Estos problemas son por lo general más difíciles de resolver y también más «costosos», en el sentido de requerir controles de mayor tamaño, véase [6].
Para saber más (II): Algunas referencias
- D.P. Bertsekas. Dynamic programming and and optimal control, Vol. I and Vol. II. Athena Scientifc, Belmont, MA, 2012 and 2017.
- S. Anita, V. Arnautu, V. Capasso. An introduction to optimal control problems in life sciences and economics. From mathematical models to numerical simulation with MATLAB, Birkhäuser/Springer, 2011.
- J. Blot, N. Hayek. Infinite-horizon optimal control in the discrete-time framework. Springer, New York, 2014.
- R. Kamalapurkar, P. Walters, J. Rosenfeld, W. Dixon. Reinforcement learning for optimal feedback control. A Lyapunov-based approach. Springer, Cham, 2018.
- E.B. Lee, I. Markus. Foundations of optimal control theory. John Wiley \& Sons, Inc., New York-London-Sydney, 1967.
- J.-M. Coron. Control and nonlinearity, American Mathematical Society, Providence, RI, 2007.

Dejar una contestacion