Publicamos la solución al divertimento de circunferencias divertidas. Muchas gracias a Renato Álvarez y Niurka Rodríguez, Anónimo17, Ángel Jáñez y Magdalena Jáñez por las soluciones parcialmente correctas que nos han enviado.
Divertimento:
Llamamos divertido a un conjunto finito de circunferencias si satisface que cada una de ellas es tangente exactamente a otras cinco, ninguna de ellas se corta con cualquier otra y no hay tangencias entre más de dos circunferencias. ¿Existe un conjunto divertido de \(2024\) circunferencias? ¿Y de \(2025\)?
Solución:
La imagen de abajo muestra un conjunto divertido de \(22\) circunferencias. Como \(2024=92·22\), reuniendo \(92\) copias distintas de dicho arreglo respondemos afirmativamente a la pregunta.
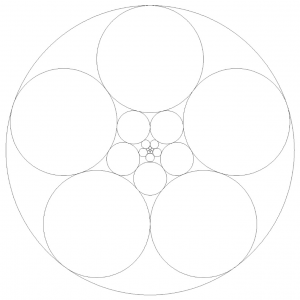
Por otro lado, no hay ningún conjunto divertido con \(2025\) circunferencias, ni con ninguna otra cantidad impar de ellas. En efecto, supongamos que dicho arreglo está formado por \(n\) circunferencias, y consideramos los pares \((C,P)\) formados por una circunferencia de ellas y un punto de tangencia de dicha circunferencia \(C\). Como \(C\) toca exactamente a cinco circunferencias, habrá \(5n\) pares. Por otro lado, para cada punto \(P\) habrá exactamente dos pares con él en la segunda componente. Por tanto, el número total de pares debe ser par (valga la redundancia), pero \(5n\) no puede ser par si \(n\) es impar.
El resultado que aparece en este divertimento se puede ampliar si utilizamos una idea que ha aportado Anónimo17 en su solución. Como vemos en la siguiente imagen, se puede encontrar un conjunto divertido con una cantidad menor de circunferencias que el que aparece en la Figura 1, concretamente, con \(12\) circunferencias. Si encajáramos esta misma figura dentro (o fuera) de sí misma, eliminando, a su vez, la circunferencia en la que se encaja, obtendríamos el conjunto divertido que aparece en la Figura 1. Iterando este proceso, se puede construir cualquier conjunto divertido que contenga \(10k+2\) circunferencias.


En el dibujo del modelo 12 hay un pequeño giro en la parte interna que haría que no se cumpla el enunciado. La primera corona circular, la más interna, debiera encajar cada círculo entre cada dos de la siguiente. Viene a ser el modelo de 22 y la parte más interna sustituida por un sólo círculo.
Corregido, Anonimo17, ¡muchas gracias por el aviso!