Como ya hemos contado la interpretación probabilística de la Mecánica Cuántica propuesta por Max Born en su trabajo “Zur Quantenmechanik der Stossvorgänge” (Sobre la mecánica cuántica de los procesos de colisión) de 1926 no fue precisamente bien acogida por la mayoría de los físicos de la época siendo Einstein su principal crítico. La razón fundamental era que se se perdía la descripción causal de los fenómenos, es decir la teoría no podía responder a la pregunta ¿Cuál es el resultado de la medición? sino ¿cuán probable es un resultado específico de una medición? De hecho el propio Born era consciente de lo que ello implicaba y en su artículo escribía
Aquí surge todo el problema del determinismo. Desde el punto de vista de nuestra mecánica cuántica, no hay ninguna magnitud que en cada caso determine causalmente el resultado de la colisión; pero tampoco experimentalmente por el momento tenemos ninguna razón para creer que existan algunas propiedades internas del átomo que condicionen un resultado definitivo para la colisión. […] Yo mismo me inclino a renunciar al determinismo en el mundo de los átomos. Pero esa es una cuestión filosófica para la que los argumentos físicos por sí solos no son decisivos.
Einstein se negaba a aceptar dicha interpretación como evidencia su famosa frase Dios no juega a los dados, que ya forma parte de nuestro acervo cultural, aunque casi siempre mal interpretada. En esta entrada, tal y como prometimos aquí, discutiremos el último intento de Einstein por demostrar su punto de vista.
Comenzaremos nuestra historia en octubre de 1927, durante la famosa conferencia 5ª Solvay que ya mencionamos aquí y que reunió a la crema de la física teórica del momento en Bruselas para debatir el tema Electrones y fotones, que traducido al lenguaje moderno significaba discutir la recién formulada mecánica cuántica.

Durante esa conferencia, según cuenta Heisenberg, más que a las charlas en sí mismas todos terminaron pendientes del duelo entre Bohr y Einstein sobre la interpretación de la Mecánica cuántica. Este fue su relato
Las discusiones se centraron pronto en el duelo entre Einstein y Bohr sobre la cuestión de hasta qué punto la teoría atómica en su forma actual podía considerarse la solución final de las dificultades que se habían discutido durante varias décadas. Generalmente nos encontrábamos en el hotel a la hora del desayuno y Einstein comenzaba a describir un experimento mental [Gedanken] en el cual, según él, las contradicciones internas de la interpretación de Copenhague [la interpretación probabilística de la función de onda] eran claramente visibles. […] Bohr generalmente terminaba el análisis completo del experimento mental a última hora de la tarde y se lo mostraba a Einstein durante la cena. Einstein no tenía ninguna buena objeción a su análisis, pero en el fondo [de su corazón] seguía sin estar convencido.
Esta situación (el duelo entre Bohr y Einstein) se prolongó durante años pues, según contó Otto Stern en la 6ª Conferencia Solvay de 1931 la situación volvió a repetirse, solo que ya no era en centro de la atención de todos como lo fue en 1927.
Fue en esa conferencia de 1931 (como contó Bohr años después) donde a Einstein se le ocurrió un experimento mental para mostrar que la relación de incertidumbre de Heisenberg fallaba y que puso en gran aprieto a Bohr, pero este, con un tremendo golpe de efecto a la postre le desmontó el razonamiento a Einstein usando la teoría general de la relatividad del propio Einstein. Tras esta aparente derrota Einstein claudicó y aceptó que la nueva mecánica cuántica era consistente, pero nunca la consideró una teoría completa.
Para entender de lo que estamos hablando veamos un ejemplo sencillo debido al físico David Bohm. Imaginemos una partícula, por ejemplo un electrón, cuyo estado esté definido por la siguiente función de onda
$$
\Psi=\frac{1}{\sqrt{2}}|\!\uparrow \rangle+\frac{1}{\sqrt{2}}|\!\downarrow \rangle,
$$
donde \(|\!\uparrow \rangle\) es el estado correspondiente al espín up \(\uparrow\) y \(|\!\downarrow \rangle\) al espín down \(\downarrow\).
Cuando medimos el espín de la partícula únicamente obtendremos uno de los valores \(\uparrow\) o \(\downarrow\). Solo realizando una gran cantidad de mediciones de energía descubriremos que en un 50 por ciento obtendremos uno u otro resultado. Eso es lo más que puede explicar la mecánica cuántica.
Pero supongamos ahora, como razonaba Bohm, que las partículas se producen siempre por pares, una con espín \(\uparrow\) y la otra con espín \(\downarrow\). Esto es lo que ocurre, por ejemplo, en la descomposición del mesón neutral \(\pi^0\) en un electrón y un positrón. Supongamos que el pión está en reposo y que tras la descomposición el electrón va en una dirección y el positrón en otra. Como el pión \(\pi^0\) tiene espín cero, entonces si el electrón tiene espín \(\uparrow\) (o \(\downarrow\)), el positrón necesariamente tiene que tener el espín contrario \(\downarrow\) (o \(\uparrow\)) pues se tiene que conservar el momento angular total. De esta forma, el estado del electrón y el positrón vendrá descrito por la función de onda
$$
\Psi_\pm=\frac{1}{\sqrt{2}}|\!\uparrow \rangle_A \otimes |\!\downarrow \rangle_B \pm\frac{1}{\sqrt{2}}|\!\downarrow \rangle_A\otimes|\!\uparrow \rangle_B,
$$
donde el subíndice \(A\) lo asociaremos al electrón y el \(B\) al positrón. Este estado es lo que se llama un estado entrelazado, término introducido por Schrödinger en 1935 e inspirado por el trabajo de ERP del que hablaremos en breve. Nótese que en cada descomposición de un mesón \(\pi^0\) se obtendrá un electrón y un positrón pero a priori no sabemos que espín tendrá cada uno (hay un 50% de posibilidades), pero lo que si sabemos es que las mediciones del espín de cada partícula están correlacionadas: sabiendo el espín de
una sabremos instantáneamente el espín de la otra.
En efecto, imaginemos que tras la descomposición cada partícula vuelan hasta los laboratorios de un par de amigos que llamaremos Alice y Bob. Cuando cada uno recibe su partícula no sabe cuál es su espín, así que han de asumir que su partícula se encuentra en el estado \(\Psi\) descrito antes. Solo al medir el espín de su partícula Alice (o Bob) sabrá si esta tiene espín \(\uparrow\) o \(\downarrow\). Hasta aquí no hay mucho problema, el problema viene del hecho de saber que como siempre se generan dos partículas, una con espín \(\uparrow\) y la otra con espín \(\downarrow\), entonces, tan pronto Alice (o Bob) realice su medición no solo sabrá el espín de su partícula, sino el de la de su colega Bob (o Alice).
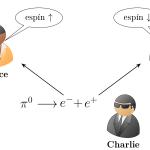
¿Por qué es eso un problema? Pues porque la teoría de la relatividad nos dice que no se puede trasmitir información a velocidad mayor que la de la luz y cuando uno de los dos amigos, Alice o Bob, hagan su medición, automáticamente sabrán lo que tiene el otro, independientemente de si sus laboratorios están a una distancia de 100 metros o en los extremos de la galaxia. Eso es lo que llamó Einstein spukhafte Fernwirkung, una acción fantasmal a distancia y eso no le gustaba nada a los físicos y especialmente a Einstein.
Antes de seguir conviene resaltar dos conceptos importantes que no están solamente relacionados con cuestiones físicas sino también con cuestiones filosóficas. Son el concepto de realidad física y el de localidad.
Esto es importante pues la interpretación de la mecánica cuántica mayoritariamente aceptada postulaba que solamente tenía sentido hablar del estado del sistema o de una determinada magnitud física tras medirla: solo existe lo que se puede medir. En palabras de Heisenberg
Para conocer el estado de un objeto, es necesario observarlo. Esta observación implica una interacción entre el observador [es decir, el sujeto] y el objeto, que modifica al objeto. Para las partículas pequeñas, la interacción se vuelve tan fuerte que la observación a menudo implica su destrucción. Bohr ha acuñado el concepto de «complementariedad» para describir la situación de forma más apropiada. Un conocimiento preciso de la velocidad [de la partícula] excluye un conocimiento preciso de [su] posición; el primero es complementario del segundo. O bien, la descripción causal de un sistema es complementaria de la descripción espacio-temporal del mismo sistema. Porque, para obtener una descripción espacio-temporal, es necesario observar, y esta observación perturba el sistema. Si el sistema se perturba, ya no podemos seguir su conexión causal de manera pura [exacta, sin adulterar] … [En consecuencia], el simple concepto determinista de la naturaleza que existía en la física [clásica] anterior ya no puede llevarse a cabo. La interacción entre el observador y el objeto hace imposible una conexión causal clara.
Algunos incluso iban más allá como Jordan, otro de los tres hombres (como le llamaban cariñosamente los físicos a los padres de la mecánica matricial: Born, Heisenberg y Jordan) quien afirmaba que
Las observaciones no sólo alteran lo que se debe medir, sino que producen la propia medición … Obligamos [al electrón] a asumir una posición definida … Nosotros mismos producimos los resultados de la medición.
Pues bien, Einstein (y otros muchos físicos de la época) defendía que las propiedades de un sistema físico existen independientemente de cualquier medición, es decir existe una realidad de verdad, y las propiedades y los objetos son reales, es decir, existen al margen de que podamos medirlos. Como le preguntaría Einstein durante un paseo a Abraham Pais -físico, historiador de la ciencia y biógrafo de Einstein- alrededor de 1950: ¿Realmente crees que la Luna solo existe cuando la estás mirando?
Lo siguiente en que todos estaban de acuerdo era que dicha realidad era siempre una realidad local, es decir, ni los cambios en un sistema físico dado ni la información pueden propagarse instantáneamente a otros lugares del Universo. Eso entraría en contradicción con la teoría de la relatividad.
¿Cuáles son las implicaciones de lo anterior? Pues que si tenemos una teoría local-realista las mediciones no pueden influir en los objetos de estudio ni en sus propiedades (la partícula siempre tendrá espín \(\uparrow\) o \(\downarrow\) independiente de que lo midamos o no), algo que como hemos dicho no tenía en cuenta la interpretación ortodoxa de la mecánica cuántica..
Lo que Einstein afirmaba era que la mecánica cuántica no era una teoría completa, es decir, había ciertas propiedades que, o bien no se estaban considerando, o que ni siquiera se conocían: las famosas variables ocultas. Según él, si tuviésemos toda la información no habría esas indeterminaciones, todo volvería a ser causal como era la física clásica. Resumiendo, según Einstein la cuántica no era una teoría completa pues no aceptaba que fuese una teoría no local-realista. Eso lo dejó plasmado en una carta a Max Born en marzo de 1947 donde afirmaba
No puedo creer seriamente en [la teoría cuántica] porque no puede conciliarse con la idea de que la física debería representar una realidad en el tiempo y el espacio, libre de acciones fantasmales a distancia.
Para mostrar su punto de vista describió un experimento mental que pasó a la historia como la paradoja de EPR (Einstein-Podolsky-Rosen) que publicó con Podolsky y Rosen en 1935. En dicho artículo Einstein, Podolsky y Rosen de 1935 comenzaban definiendo rigurosamente lo que para ellos significaba una realidad física:
Si, sin perturbar de ninguna manera un sistema, podemos predecir con certeza absoluta (es decir, con una probabilidad igual a uno) el valor de una cantidad física, entonces existe un elemento de realidad física correspondiente a dicha cantidad física.
A continuación razonaban, usando dos sistemas con posiciones y momentos (velocidades) dados, y mediante una construcción muy ingeniosa, que la función de onda del sistema compuesto no puede describir completamente la realidad, luego la teoría cuántica tal y como estaba formulada no era una teoría completa. De hecho, la función de onda propuesta en EPR describía un estado entrelazado como el que escribimos antes solo que más complicado.
Antes de terminar esta entrada conviene hacer notar que aunque el experimento propuesto por Bohm descrito antes es mucho más sencillo que el que describen Einstein, Podolsky y Rosen, las conclusiones son de ambos son equivalentes. En efecto, como al medir Alice (o Bob) el espín de su partícula sabe inmediatamente el resultado de la medición del otro, y está claro que como pueden estar tan alejados como quieran no hay forma de que la medición de uno pueda perturbar la del otro. Eso implica que el espín es una propiedad real de la partícula y tiene un valor independientemente de que se mida o no. Pero como ya vimos antes, cuando uno de ellos mide el espín de su partícula automáticamente sabe el resultado de la medición del otro, es decir se viola la localidad y aparece la acción fantasmal a distancia que tan poco gustaba a Einstein. Esa posibilidad de hacer una predicción simultánea hace que la realidad de un sistema dependa del proceso de medición realizado en el otro sistema que no perturba en modo alguno al primer sistema, algo que, en palabras de EPR: No se podría esperar que ninguna definición razonable de la realidad permitiera esto.

Aunque la respuesta de Bohr al artículo EPR no tardó demasiado, esta no fue lo suficientemente clarificadora como las veces anteriores, de hecho durante casi 30 años dio para muchas discusiones filosóficas. Así que, llegados a este punto no nos queda más remedio que preguntarnos si, efectivamente, la mecánica cuántica es una teoría completa, como defendían Borh, Heisenberg, Pauli, Jordan, etc. o era incompleta como afirmaba Einstein, Schrödinger, entre otros.
Obviamente la afirmación la mecánica cuántica no es una teoría completa es imposible de rebatir sin experimentos concretos (nuestro bendito método científico). Así que ¿cómo salir de este embrollo? Eso amigo lector lo descubriremos en la próxima entrada.
Para saber más:
En el Capítulo 12 de [1] hay una descripción muy detallada del experimento mental de Bohm y de como se solucionó la pregunta final de nuestra entrada que, como hemos prometido, aparecerá en a siguiente entrada del blog. La referencia [2], como siempre es una fuente inagotable y bien documentada de los inicios de la mecánica cuántica, en particular en el Capítulo II, sección 6 se puede encontrar una detallada descripción de lo que ocurrió en las Conferencias Solvay de 1927 y 1930.
[1] Griffiths DJ F. Schroeter – Introduction to Quantum Mechanics 3rd Edition, Cambridge University Press (2018).
[2] Jagdish Mehra, Helmut Rechenberg-The Historical Development of Quantum Theory. Vol. 6. The Completion of Quantum Mechanics 1926-1941 Partes 1 y 2. Springer (2000)
Como anécdota curiosa vale la pena incluir lo, que según Heisenberg, Ehrenfest, amigo de Bohr e íntimo amigo de Einstein, le dijo a este último durante una de las famosas discusiones entre Einstein y Bohr en la Conferecia Solvay de 1927: <<Me avergüenzo de ti, Einstein. Estás aquí exactamente en la misma posición que tus oponentes en sus inútiles intentos de refutar tu teoría de la relatividad>>.

Dejar una contestacion