Este divertimento forma parte del concurso de 2024. Puedes encontrar las bases en este enlace.
Delantal:
Se han escrito ríos de tinta sobre la relación entre las matemáticas y el arte, pasando por el estudio de las proporciones humanas, las propiedades de los mosaicos, el número áureo o el uso de proyecciones y perspectivas; y desde otro punto de vista, quizá sólo accesible a los matemáticos, se podría describir la actividad matemática en sí misma, en la búsqueda de nuevas relaciones y en la construcción de estructuras y demostraciones, como una forma de arte, como ya sugería G. H. Hardy al afirmar que «La belleza es la primera piedra de toque; en el mundo no hay un lugar permanente para las matemáticas desagradables desde el punto de vista estético.» El problema que planteamos hoy nos deja en la orilla de la influencia de las matemáticas en el arte, pues los cuadrados que tenemos que contar, bien escogidos y dotados de color con criterio, podrían dar lugar a una composición similar a las del artista holandés Piet Mondrian, quien fuera inspiración e influencia del movimiento Bauhaus, y autor de la imagen en la miniatura que acompaña a esta entrada.
Divertimento:
Consideremos tres números \(m\), \(n\) y \(p\), primos, distintos y mayores que 2, de modo que la cuadrícula formada por \(m\) rectas verticales y \(n\) rectas horizontales contiene en total \(p\) cuadrados de tamaños distintos. ¿Cuáles son los valores posibles de \(p\), \(m\) y \(n\)?
Observación: en la cuadrícula de la imagen, que contiene \(n=4\) rectas horizontales y \(m=5\) rectas verticales (representadas de forma discontinua), se han señalado tres cuadrados de tamaños diferentes.
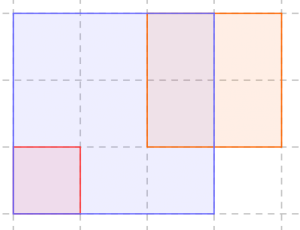
Esta cuadrícula contiene 12 cuadrados de lado igual a uno, 6 cuadrados de lado igual a dos y 2 cuadrados de lado igual a tres, de donde \(p=20\) (y no es solución del problema propuesto).
Actualización 7/11/24: se ha añadido una aclaración al enunciado del problema.
Solución:
Puedes enviar tus soluciones hasta el viernes 15 de noviembre a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el lunes 4 de noviembre. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.

Una pequeña duda. La cuadrícula expuesta sería de 3*4 si nos referimos a «longitudes» y se comenta 4*5 segmentos. ¿O serían puntos? Para tener claro si los valores primos se refieren a una u otra cosa.
La cuadrícula determinada por 4 rectas horizontales y 5 verticales forma un rectángulo de lados 3 y 4 unidades. Los valores primos de m y n son el número de rectas.
Se ha editado esta respuesta para añadir una aclaración.