Solución: cuadrados en una cuadrícula

Publicamos la solución al divertimento Cuadrados en una cuadrícula. En esta ocasión, hemos recibido respuestas correctas de Anónimo17, Renato Álvarez Rodríguez y Niurka Rodríguez Quintero, F. Damián Aranda Ballesteros, Don Diedro y Don Pablo, Magdalena Jáñez, Antonio Medinilla y David Ramos y Ruben Rios Mallqui.

Divertimento:

Consideremos tres números \(m\), \(n\) y \(p\), primos, distintos y mayores que 2, de modo que la cuadrícula formada por \(m\) rectas verticales y \(n\) rectas horizontales contiene en total \(p\) cuadrados de tamaños distintos. ¿Cuáles son los valores posibles de \(p\), \(m\) y \(n\)?

Observación: en la cuadrícula de la imagen, que contiene \(n=4\) rectas horizontales y \(m=5\) rectas verticales (representadas de forma discontinua), se han señalado tres cuadrados de tamaños diferentes.

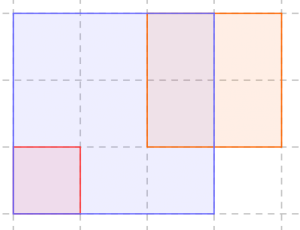
Esta cuadrícula contiene 12 cuadrados de lado igual a uno, 6 cuadrados de lado igual a dos y 2 cuadrados de lado igual a tres, de donde \(p=20\) (y no es solución del problema propuesto).

Solución:

Podemos suponer que \(m>n\) porque \(p,m,n\) son distintos (el caso \(n<m\) se corresponde con un rectángulo simétrico). Por otra parte, el número de cuadrados \(p\) es mayor que ambos números \(m\) y \(n\). Por tanto, \(p>m>n\).

Como \(m > n\), la cuadrícula formada por \(m\) segmentos verticales y \(n\) segmentos horizontales contiene, para cada valor de \(k \in \{1,\ldots,n-1\}\), exactamente \((m-k)(n-k)\) cuadrados de lado igual a \(k\). Por tanto, el número total de cuadrados es
$$
\sum_{k=1}^{n-1} (m-k)(n-k).
$$
Puede demostrarse por inducción que, para cualquier \(m\), si \(n<m\) se tiene que
$$
\sum_{k=1}^{n-1} (m-k)(n-k) = \frac{1}{6}(3m-n-1)(n-1)n.
$$
El valor de esta suma es un número primo \(p\), de modo que
$$
(3m-n-1)(n-1)n=2 \cdot 3 \cdot p,
$$
y por tanto \(n|2 \cdot 3 \cdot p\). Como además \(n\) y \(p\) son primos, se concluye que \(n=2\), \(n=3\) o \(n=p\). Pero el único caso posible es \(n=3\) por las condiciones del problema. Se deduce que
$$3m-4=p.$$
Los valores posibles de los números que se piden se corresponden con las ternas de la forma \((p=3m-4,m,n=3)\) con \(m\) y \(3m-4\) primos; por ejemplo, (11, 5, 3), (17, 7, 3), (29, 11, 3), (47, 17, 3), (53, 19, 3), (83, 29, 3), (89, 31, 3), (107, 37, 3), etc.
Desconocemos si existen una cantidad infinita de ternas con \(p=3m-4\) y \(m\) primos (agradeceríamos que, si algún lector conoce la respuesta, nos la haga llegar).