Solución: El salvapantallas del DVD

Publicamos la solución al divertimento de El salvapantallas del DVD. Muchas gracias a Antonio Medinilla Garófano y David Ramos Orozco, Renato Álvarez Rodríguez y Niurka Rodríguez Quintero y Rubén Ríos Mallqui por las soluciones que nos han enviado.

Divertimento:

Conectamos un reproductor de DVD a un televisor con una pantalla de 20 pulgadas de diagonal y formato 4:3. Pasados unos minutos, se activa el salvapantallas del reproductor y aparece un logotipo cuadrado cuyos lados miden 3 pulgadas. Inicialmente, el logotipo no toca ninguno de los bordes de la pantalla, y comienza a desplazarse con un ángulo de de 45º respecto al borde inferior. El logotipo rebota cada vez que toca uno de los bordes y mantiene sus lados paralelos a éstos en todo momento.

¿Es posible determinar si el logotipo tocará o no una de las esquinas de la pantalla?

Solución:

Como la pantalla tiene formato 4:3, sus lados son de la forma \(4x\) y \(3x\). Se cumple que $$ (4x)^2+(3x)^2=20^2,$$ de donde \(x=4\). Por tanto, los lados de la pantalla miden \(16\) y \(12\) pulgadas.

Sea \(P\) el centro del cuadrado en el momento en que aparece. La posición de \(P\) en la pantalla determina completamente la trayectoria del cuadrado. Observamos que, cuando el cuadrado toca uno de los bordes de la pantalla, el centro siempre se encuentra a \(1.5\) pulgadas de éste.

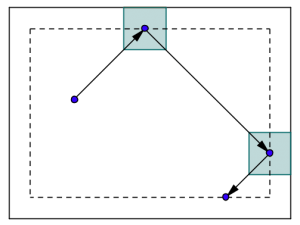
Así podemos simplificar el problema: consideramos la trayectoria que describe el punto \(P\) al moverse en el interior de un rectángulo de lados \(16-2\cdot 1.5=13\) y \(12-2\cdot 1.5=9\) pulgadas. El cuadrado toca una esquina precisamente cuando el punto coincide con uno de los vértices del rectángulo. Vamos a considerar un sistema de referencia con el origen en el extremo inferior izquierdo del rectángulo \(13 \times 9\), y denotaremos por \(P=(p_x,p_y)\) a las coordenadas del centro del cuadrado en el momento inicial.

Por otra parte, la trayectoria del punto rebotando en el interior del rectángulo es equivalente, mediante simetrías, a la que describe al desplazarse en línea recta sobre el plano con una teselación de rectángulos de dimensiones \(13\times 9\).

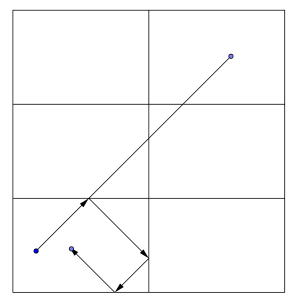
De este modo, el cuadrado tocará una de las esquinas si y sólo si la recta \(r\), que pasa por \(P=(p_x,p_y)\) con pendiente igual a \(1\), cuya ecuación es \(y-x=p_y-p_x\), contiene algún punto de la forma \((13m,9n)\) con \(m\), \(n\) enteros y positivos. En tal caso, \(m+n\) coincide con el número de veces que rebota en los bordes.

Ahora bien, \(r\) pasa por el punto \((13m,9n)\) si y sólo si \(9n-13m=p_y-p_x\). Por la identidad de Bézout, \(9n-13m\) toma cualquier valor entero cuando \(m,n\) son enteros positivos. Se concluye que el cuadrado tocará una de las esquinas si y sólo si el punto \(P=(p_x,p_y)\) pertenece inicialmente a una de las rectas \(r_k:y-x=k\) para \(-12 \leq k \leq 8\). Los vértices del rectángulo quedan excluidos porque el cuadrado no comienza tocando ninguno de los bordes de la pantalla.

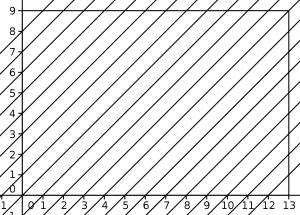
Adicionalmente, se puede hallar el número máximo de rebotes que daría el logo en caso de acabar tocando una esquina. Para ello, estudiamos cuál es el primer punto de la forma \((13m,9n)\) con coordenadas positivas por el que pasa cada recta \(r_k\).

La recta \(r_k:y-x=k\) pasa por el punto \((13m,9n)\) si y sólo si \(9n-13m=k\). Como una solución particular de esta ecuación diofántica es \(n=3k\) y \(m=2k\), tenemos que todas las soluciones son de la forma $$n=3k+13\alpha,\quad m=2k+9\alpha, \qquad \alpha \in \mathbb{Z}.$$

Para cada \(k\), sea

$$\alpha_k=\min \{ \alpha \in \mathbb{Z} : n=3k+13 \alpha>0, m=2k+9\alpha>0\},$$

es decir, \(\alpha_k\) es el valor del parámetro \(\alpha\) para el que se obtiene el primer punto de coordenadas positivas de la forma \((13m,9n)\) por el que pasa \(r_k\). Denotamos \(n_k=3k+13\alpha_k\) y \(m=2k+9\alpha_k\) a los valores correspondientes de \(n\) y \(m\).

El problema consiste ahora en determinar el valor de \(k\) para el que se obtiene el máximo de \(n_k+m_k\).

• Si \(-12\leq k \leq -9\), entones \(\alpha_k=3\). El mayor valor de \(n_k+m_k\) en este caso es \(n_{-9}+m_{-9} =21\).
• Si \(-8 \leq k \leq -5\), entonces \(\alpha_k=2\). El mayor valor de \(n_k+m_k\) en este caso es \(n_{-5}+m_{-5} =19\).
• Si \(-4 \leq k \leq -1\), entonces \(\alpha_k=1\). El mayor valor de \(n_k+m_k\) en este caso es \(n_{-1}+m_{-1} =17\).
• Si \(k=0\), entonces entonces \(\alpha_0=1\). En este caso, \(n_0+m_0=22\).
• Si \(1 \leq k \leq 4\), entonces \(\alpha_k=0\). El mayor valor de \(n_k+m_k\) en este caso es \(n_{4}+m_{4} =20\).
• Si \(5 \leq k \leq 8\), entonces \(\alpha_k=-1\). El mayor valor de \(n_k+m_k\) en este caso es \(n_{8}+m_{8} =18\).

Vemos que, efectivamente, la recta \(r_0:y-x=0\) pasa por el punto de coordenadas \((13 \cdot m_0,9\cdot n_0)=(13 \cdot 9, 9 \cdot 13)\).

Un punto que comience sobre \(r_0\) tocará una esquina después de rebotar \(22\) veces sobre los lados del rectángulo. Por tanto, podemos afirmar que, si después de \(22\) rebotes no ha llegado a una esquina, entonces el logo nunca va a tocar ninguna.