Este divertimento forma parte del concurso de 2024. Puedes encontrar las bases en este enlace.
Delantal:
En el problema que traemos hoy, con el que cerramos el año y la presente edición del concurso de nuestra sección, se propone encontrar el camino más corto entre dos puntos del interior de una isla circular, pasando por algún punto de la orilla. Aunque el desafío es interesante y la pregunta legítima -quizá fruto la necesidad de optimizar algún proceso o únicamente de la curiosidad- es inevitable pensar que sería preferible evitar el camino más corto, para así poder deambular libremente por la isla imaginaria que encierra la circunfencia, y hacer camino al andar; bien pensado, resulta más interesante considerar el camino más largo en lugar del más corto. No podemos concluir el delantal sin observar que, como en ocasiones anteriores, el problema resulta adecuado para discutir o pensar en una servilleta, en caso de que sea necesario amenizar alguna comida o reunión familiar.
Divertimento:
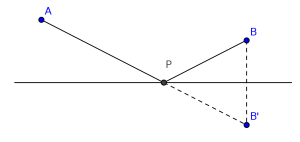
Es muy conocido el problema de encontrar el camino más corto entre dos puntos A y B situados en la misma margen de un río rectilíneo pasando por la orilla, así como la construcción geométrica, basada en la simetría axial, que indica el punto de la orilla donde se debe llegar al río.
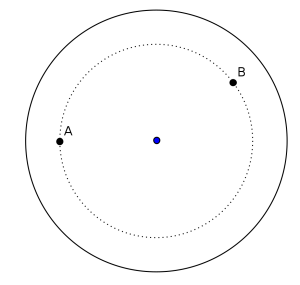
Se nos ha ocurrido preguntarnos cómo sería el problema si el río rectilíneo se cambia por una circunferencia. Supongamos que hay una isla circular donde hay dos puntos A y B situados a la misma distancia del centro. Se trata de determinar el camino más corto para llegar desde A hasta B pasando por la orilla, indicando una construcción para determinar el punto P de la orilla por donde se debe pasar.
Solución:
Puedes enviar tus soluciones hasta el viernes 10 de enero a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el lunes 13 de enero. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.

Dejar una contestacion