Today we comment on the article On the Erdös-Szekeres convex polygon problem by Andrew Suk published online in the Journal of the American Mathematical Society.
Before commenting on the content of the article, we will look at the interesting story of the problem that Suk solves (almost) completely.
The Anonymous group
In the spring of 1929 a group of mathematics students meet every Wednesday at the foot of the statue of Anonymous in the Budapest Park to discuss mathematics and solve the problems in Pólya and Szego’s book, Aufgaben und Lehrsätze aus der Analysis (Problems and Theorems of Analysis), Springer, Heidelberg, 1925.

They followed the advice of their teacher Pál Veress. The initial group consisted of Pál Turan, Márta Wachsberger and Eszter Klein. It soon was joined by György Szekeres, Miklós Ság, and the following year by Pál Erdös, Tibor Grünwald and others.
These were difficult times, since in March 1920 the fascist Horthy had come to power and unleashed a wave of anti-communism and anti-Semitism. Edward Teller, John von Neumann and the physicists Leo Szilard and Eugene Wigner, among many other Jews, emigrated to Germany, only to have to emigrate to the United States a few years later. In the autumn of 1939, they decided to inform President Roosevelt about the possibility of Hitler building an atomic bomb, and convinced Einstein to sign and send Roosevelt a letter, which is now famous, and which eventually launched the Manhattan Project.
It is known that Erdös used a special language. The Anonymous group often talked politics as well, but they all moved in the long-wave spectrum (red in Erdös’ dialect).
They did not only solve problems from the book; they soon started to raise their own problems. This love of problems is a characteristic of mathematicians. We find it in the Scottish Café problems in Lwow, and in these Budapest meetings the pattern is repeated (for the history of the Scottish Café, see the entries Stories of the Scottish Café: 1. Steinhaus and Banach, Stories of the Scottish Café: 2. The Mathematical Gathering, Stories of the Scottish Café: 3. The Scottish Notebook, Stories of the Scottish Café: 4. The Scottish Notebook Awards, Stories of the Scottish Café: 5. Wartime Gatherings and Stories of the Scottish Café: and 6. Feeding Lice).
One evening Eszter Klein came up with a new type of problem, starting from an observation of 5 points in the plane in general position (i.e. no three are aligned).
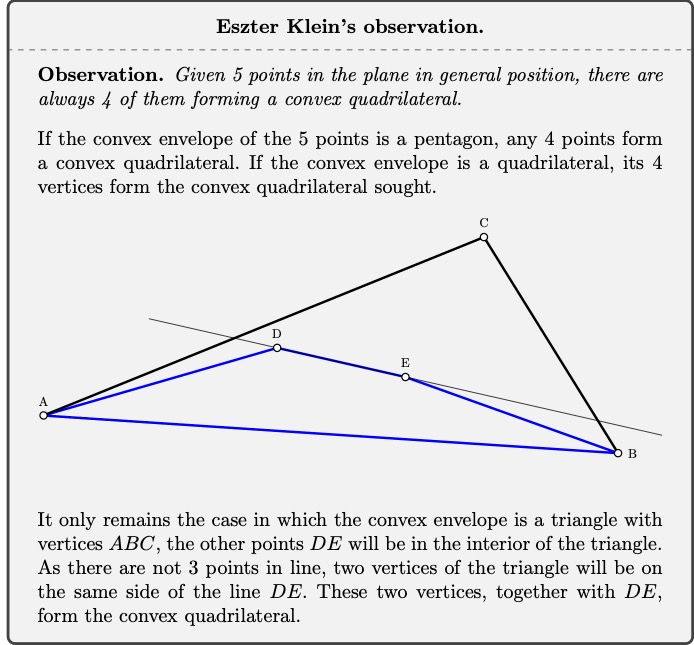 The problem posed by Eszter was the following:
The problem posed by Eszter was the following:
Given a natural number \(n\), is there a number \(N(n)\) such that any set of more than \(N(n)\) points in the plane in general position contains \(n\) points that are the vertices of a convex polygon?
At once the group saw that this was a new kind of problem. Combinatorial but also geometric.
Naturally the problem is also to determine the smallest possible number \(N(n)\). It is trivial that \(N(3)=3\), Eszter’s observation proves that \(N(4)=5\) and soon one of the Anonymous members, E. Makai, presented the proof of \(N(5)=9\).
Erdös and Szekeres soon became interested in the question of the existence of \(N(n)\). Szekeres had a particular view of the problem:
We soon realised that a simple argument would not get the solution.
We had found a new kind of geometric problem, we were eager to solve it.
For me, the fact that Epszi had proposed it [Erdös called Eszter so, short for epsilon] added a strong incentive to be the first to solve it. After a few weeks I was able to address Erdös with a triumphant
“E.P. open your wise mind”.
(Szekeres)
Szekeres then proved the existence of \(N(n)\). But his solution gave for \(N(n)\) an absurdly large value. He had rediscovered a Ramsey theorem. Nevertheless, his work ended in a wedding. Eszter and György married shortly after the paper appeared:
[1] P. Erdös y G. Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935) 463–470.
This is why Erdös called it The Happy End Problem.

This paper contains a second proof of the finiteness of \(N(n)\) which provides an improvement in the upper bound
$$N(n)\le {2n-4\choose n-2}+1.$$
Moreover, they formulate a conjecture with a naivety that leaves me astonished, so much so that I repeat their words in [1] presenting the conjecture
It is remarkable that \(N(3)=3=2+1\), \(N(4)=5=2^2+1\), \(N(5)=9=2^3+1\).
We can therefore conjecture that \(N(n)=2^{n-2}+1\), but the bounds given by our theorems are much larger.
(Erdös and Szekeres)
Can one imagine a lesser basis for a conjecture! However, Erdös and Szekeres came back 26 years later to publish on the question
[2] P. Erdös y G. Szekeres, On some extremum problem in elementary geometry, Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 3-4 (1961) 53–62.
They construct for each \(n\) a set of \(2^{n-2}\) points that do not contain \(n\) points that are vertices of a convex polygon. That is, they prove that
$$N(n)> 2^{n-2}.$$
This greatly strengthens the conjecture and brings us to the main issue.
Erdös-Szekeres problem: We know that
$$2^{n-2}+1\le N(n)\le {2n-4\choose n-2}+1.$$
What is the true value of \(N(n)\)? Is it as Szekeres conjectured \(N(n)=2^{n-2}+1\)?
For example in the case \(n=6\) we have the question:
Problem: We know that \(17\le N(6)\le {8\choose 4}+1=71\). Is \(N(6)=17\) actually?
Further progress on the problem until Suk’s arrival
This is a difficult problem indeed. It remained dormant for 37 years until its appearance in [3], the result of a long plane trip by another pair of mathematicians.
[3] F. R. L. Chung y R. L. Graham, Forced convex \(n\)-gons in the plane, Discrete Comput. Geom. 19 (1998) 367–371.
Chung and Graham manage to lower the upper bound of Szekeres and Erdös by the beautiful amount of \(1\). In other words, they prove that
$$N(n)\le {2n-4\choose n-2}.$$
This is something, but note that the lower bound is of the order of \(2^n\) and the upper bound is worth about \(4^n/\sqrt{n}\); the difference between the two is so great that to take one unit off seems too little. In our little problem this is \(17\le N(6)\le 70\).
But the release of [3] triggered a cascade of publications:
D. Kleitman and L. Pachter in the same volume as [3] but a few pages further on, prove
$$N(n)\le {2n-4\choose n-2}-2n+7.$$
G. Tóth and P. Valtr a few weeks later and a few pages further on in the same volume of the journal reduce the above result by about half
$$N(n)\le {2n-5\choose n-2}+2.$$
G. Tóth and P. Valtr 5 years later use Chung and Graham’s technique to improve their previous result by one unit!
$$N(n)\le {2n-5\choose n-2}+1.$$
So now we have \(17\le N(6)\le 36\), we are narrowing the margin.
There is a computer proof that \(N(6)=17\), by Szekeres himself, but a conceptual proof would be desirable.
Andrew Suk’s result

Last year it has appeared, but still exclusively online, the paper
[4] A. Suk, On the Erdös-Szekeres convex polygon problem, J. Amer. Math. Soc. publicado electrónicamente el 31 de Septiembre de 2016.
Suk proves that
$$ N(n)\le 2^{n+6n^{2/3}\log n}$$
for \(n\ge n_0\), where \(n_0\) is a given constant. For the first time the upper and lower bounds are of the same order.
The proof is based on many previous works. Already Erdös and Szekeres considered the points in a plane with a coordinate system and defined successions of points \(A_1\), \(A_2\), … , \(A_n\) which they called cups and caps. They form a cup if joining them by segments \(A_1—A_2— \dots —A_n\) gives the graph of a convex function (caps if the function is concave). Pór and Valtr had managed to obtain from a numerous set of points \(k\) subsets \(C_j\) each one with a fraction of the points of the total and in such a way that any selection of a point in each set \(A_j\in C_j\) gives points \(A_1\), \(A_2\), … \(A_k\) in convex position.
Suk’s work elaborates on these sets.
Hungarian Mathematics
Hungary is the country with the highest density of mathematicians. Andrew Suk is not of Hungarian descent, but the problem and his mathematical origins are indeed related to Hungary. Andrew is a professor in the Department of Mathematics, Statistics and Computer Science at the University of Illinois at Chicago, and completed his PhD thesis between (2006–2011) at the Courant Institute in New York under the direction of Janos Pach, who was also the director of Géza Tóth between (1993-1997). Janos Pach was born in Hungary and is the nephew of Pál Turan, one of the founders of the Anonymous group with which this story begins.
The success of Hungarian mathematicians is striking. It has earlier roots but it is from 1920 onwards that it exploded, names such as Fejér, von Neumann, von Karman, Haar, Pólya, Marcel and Frigyes Riesz, Szegö, Turán, Erdös, Szekeres, Lax, Rényi and many more come to mind. This success has continued through many political vicissitudes and has endured through many different periods and continues as we can see today.
It is important to understand why these differences exist between countries. In the case of Hungary, as in many others, it is in society. What society values. There are two obvious drivers
- The KöMaL journal
- La competición Eötvös.
KöMaL was founded in 1894, dedicated to young people between the ages of 14 and 18. It mainly publishes problems that have helped many scientists to develop their problem-solving skills. The best solutions are published together with the names of their young authors and every year the pictures of the best ones appear in the journal. (Nowadays they are published on the internet and we can search for the photo of Eszter Klein in the year 1925-26, Pál Erdös in 1926-27 and György Szekeres in 1927-28, or the names of the future geniuses in 2014-2015). The magazine also contains articles on interesting mathematical results.
The Eötvös (now Kürschák) competition started simultaneously with the magazine KöMaL, which prepared for it, consists of problem solving. The publication of the problems and the names of the winners was from the beginning an event of great public interest.
The problems are elementary in nature, but difficult and require ingenuity and creativity to solve. Any help in the form of books or notes is allowed. The top finishers were admitted to any university in Hungary to study mathematics.
Contrast in our country
In short: Hungarian society values talent; KöMaL magazine and the competitions detect and promote talent, it gives them obvious public recognition.
In our society other matters are valued. Sportsmen and women, chefs, saints, playboys and so on are valued. Mathematical talent (and many other talents) are treated with contempt. As misfits or madmen. In many areas there is a conspiracy of fools.
Many who see the problem of our education, believe that the remedy lies in changing the curricula. Nothing could be more contrary to reality. A curriculum needs time to find its place. The first problem of education in Spain is teachers’ salaries. Salaries are the main measure of recognition for an important job. Not so long ago, during the real estate bubble, a bricklayer earned much more than a teacher.
With decent salaries, the most qualified would go to fill that job. Nowadays, teaching is one of the careers with the fewest entry requirements and it is not necessary to have a high grade to be able to study it, so it is not unusual for some people to enter it because they cannot access other more prestigious careers, without stopping to think about whether or not they have the necessary vocation to practice it.
Learn more
A survey on the subject prior to Andrew Suk’s work:
W. Morris, y V. Soltan, The Erdös-Szekeres problem on points in convex position – A survey, Bull. Amer. Math. Soc. 37 (2000) 437–458.
After 70 years of marriage George and Esther Szekeres died within an hour of each other. George was 94 and Esther 95.
The story of the problem is told in a chapter of the book on Erdös, to be recommended:
P. Hoffman, The Man Who Loved Only Numbers. Fourth Estate, London, 1998.
An interesting lecture by Géza Tóth at the Rényi Institute is the following
The Erdos-Szekeres Theorem, and a generalization for lines.
In it he discusses a generalization for lines instead of points. In this case the solution \(N(n)\) approaches the upper bound instead of the lower one.
There are several web pages on Andrew Suk’s feat and the happy ending problem, for example:

Leave a Reply