We have devoted several of our previous posts (see here and here, for example) to explain how the attempt to understand certain natural phenomena led physicists and mathematicians in the early 20th century to propose some unorthodox theories. In this post we are going to tell the story of the discovery of atomic structure and, of course, the role that mathematics played in that discovery.

At the end of the 19th century, it was not clear how matter was constituted. While most scientists had no doubt that matter was made up of atoms, none of them had any idea what those atoms looked like. The most representative example of what was known about the subject is well described in a speech given by the eminent English chemist and physicist William Crookes at the Congress of the British Association for the Advancement of Science in 1898:
What is the atom, and is it the same atom that appears in solid, liquid or gaseous states? Each of these states involves ideas that have to do only with vast groupings of atoms. If, like Newton, we try to visualise an atom as a hard, spherical body, or, like Boscovitch and Faraday, consider it as a centre of force, or accept Lord Kelvin’s vorticial atomic theory, an isolated atom is an unknown entity difficult to conceive of.
Crookes’ statement is insightful, for indeed the atom is too small to see, but everything is made up of millions and millions of these tiny bricks. In this article we are going to tell how the first “modern” atomic model came about, the well-known “planetary” model now accepted by all and proposed by the English-based New Zealander Ernest Rutherford. So let us begin our story.

Although the first atomic models date back to the Greeks, we will start a few centuries later with the plum pudding model of J.J. Thomson, who proposed a more or less reasonable model that could quantitatively explain some of the experimental results of the time, namely: the real dimensions of atoms and that inside them there must be small particles carrying charges (which would later be called electrons, something that Thomson himself would confirm in a classic experiment with cathode rays). The best description of J.J. Thomson’s model appeared in a book entitled “Electricity and Matter” published in 1904, which Thomson himself wrote and in which he set out all his ideas on the subject.

On page 96 of Chapter V of that book, J.J. describes his plum pudding model, which stated that the atom consisted of a positively charged sphere inside which the electrons (which he still called corpuscles) were contained. The amount of total positive charge had to be equal to the sum of the charges on the electrons (because the atom was electrically neutral). Let us see what predictions this model could give us. Suppose for simplicity’s sake that we have a hydrogen atom, and assume, as was assumed at the time, that the oscillation of the electron inside the atom was responsible for the emission of electromagnetic waves of a given wavelength. Then, assuming that the positive sphere has radius \(R\), Newton’s laws in combination with Maxwell’s electrodynamics allow us to calculate the frequency of such radiation:
$$
\omega^2=\frac{e^2}{mR^3},
$$
where \(e\) is the electron charge and \(m\) its mass. If we take the frequency \(\omega\) equal to \(6\cdot 10^{-7}m\), corresponding to the visible spectrum of hydrogen, we obtain an estimate of the radius of the atom of \(3\cdot 10^{-10}m\) in perfect agreement with the experiments of the theory of gases among others. But… how to keep such a system in equilibrium? On the one hand the electrons repel each other and on the other hand they are attracted by the field generated by the positive sphere. In other words, the model had a big problem with stability, and although J.J. Thomson tried to use this flaw to explain the phenomenon of radioactivity (in chapter VI of his book), the model was eventually discarded because it was superseded by a simpler model: Ernest Rutherford’s “planetary” model. Here is its history.

It was the year 1895 when a 24-year-old New Zealand physics graduate student named Ernest Rutherford arrived in Cambridge after winning a scholarship to continue his studies in England. The setting chosen by the young Rutherford was the Cavendish Laboratory, which at the time was run by J.J. Thomson himself and was one of the best-equipped laboratories in England. At Cambridge Rutherford carried out his first research and published several articles that earned him the respect of the physicists of the time. So much so that at the age of 27, in 1898, he was offered a professorship at the University of Montreal, which he accepted. In Montreal he devoted himself to the study of radioactivity, obtaining some tremendously important results. On the one hand, Rutherford realised that the radiation emitted by uranium (and by radioactive elements in general, Becquerel’s newly discovered radioactivity) is composed of three very different types: what we know today as alpha, beta and gamma radiation. He also discovered with his colleague Frederick Soddy (an English chemist who worked for several years in Montreal) that radioactivity is accompanied by a disintegration of the elements, something completely new, since at the time it was believed that matter was indestructible. At the same time, Rutherford also deduced the famous formula for radioactive decay, which he published together with Soddy in 1902-1903. His research in Montreal won him the Nobel Prize in Chemistry “for his investigations into the disintegration of the elements and the chemistry of radioactive substances”, which is somewhat amusing, since Rutherford considered himself a physicist and is credited with the phrase “All Science is Either Physics or Stamp Collecting” (see an interesting article on this subject here)
Shortly before receiving the prize, in 1907, Rutherford left Montreal and went back to England to take charge of the Manchester Physical Laboratory, another of the world’s top laboratories. It was there that the vision of the atomic model that we accept today was accomplished. At that time Rutherford was interested in the process of diffusion of alpha particles (the ones we mentioned earlier, which are in fact helium ions), a problem that consisted of studying how alpha particles diffuse through different media, in particular through very thin films of different metals. The latter experiments were being carried out by Rutherford’s assistant at the time, Hans Geiger (the creator of the famous Geiger counter), together with Ernest Marsden, who at the time was an undergraduate student (in his final year of his degree) in Rutherford’s laboratory. The results they were obtaining were quite “odd“, they even thought that they did not make sense, because what they expected was that the trajectory of the alpha particles would vary a few degrees when they passed through the metal foil, and they had seen that sometimes the diffusion almost reached 90 degrees. The fundamental reason was that according to the plum pudding model, the deflection of the alpha particles would have to be very small, as can be seen in the following diagram:
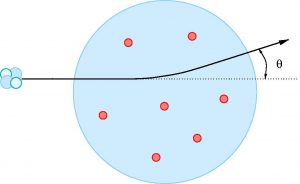

Rutherford, who usually visited the laboratory and was interested in the state of the experiments, entered the laboratory and Marsden explained the situation to him. Let Marsden himself tell the story:
Rutherford had been thinking about the matter, turned to me and said “See if you can get any effect from alpha particles directly reflected from a metallic surface”. I don’t think he expected any results, but it was one of those hunches that perhaps some effect could be observed… Rutherford was always ready to confront the unexpected and exploit it, if possible, though he also knew when to stop such explorations. Of course, I knew enough to realise that, even if what was expected was a negative result, if I let slip any positive result I would be committing an unforgivable sin. To my surprise, I was able to observe the effect I was looking for […] I remember well when I informed Rutherford of the result a week later […] A few weeks later Rutherford instructed me to prepare the results of the Geiger experiment in a form suitable for publication. [taken from Marsden’s article in “Rutherford at Manchester”, J.B. Birk ed., W.A. Benjamin, 1963].
A similar story (essentially the same, only differing in minor details) was told by Rutherford himself years later (in 1936) in a lecture entitled “Forty Years of Physics” (published in Background To Modern Science, J. Needham, Joseph and W. Pagel, eds. Cambridge University Press, 1938). On page 68 Rutherford recalled when Geiger told him that there were alpha particles scattering backwards:
It was the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch projectile at a piece of tissue paper and it came back and hit you. On consideration, I realised that this backward scattering had to be the result of a single collision, and when I did the calculations I saw that it was impossible to get something of that order of magnitude unless you took a system in which most of the mass of the atom was concentrated in a tiny nucleus. That’s when I had the idea of an atom with a tiny massive charged center.
Thus, on 19 May 1909, the Royal Society received the manuscript “On a Diffuse Reflection of the α-Particles” signed only by Geiger and Marsden, an example of honesty and generosity on the part of their boss and tutor Rutherford, who did not sign this important contribution. Why was this experiment so important? The reason is simple: the experiment ruled out the raisin-cake model because it was impossible to explain how an alpha particle fired at a metal sheet bounced off at an angle greater than 90°.

So Rutherford began to think the matter over, something that took him two years, apparently an eternity according to the point of view of many (if we measure it with today’s standards), but as Sánchez-Ron explains very well in his book “Historia de la Física Cuántica” (History of Quantum Physics), the consequences of Geiger and Marsden’s experiment were not as obvious as one might think: it was necessary to make sure that the mathematics of J. J. Thomson’s atom did not work, that is, that they could not explain such a deviation in the trajectory, and not only that, it was also necessary to prove that the new model did succeed. This is what Rutherford achieved in his paper published in May 1911 in the Philosophical Magazine (although he had presented the results at the Manchester Literary and Philosophical Society in February of the same year). At the beginning of that paper Rutherford wrote:
It has generally been assumed that the scattering that an alpha or beta beam undergoes as it passes through a thin film of matter is the result of a multitude of small scatterings by the atoms of the matter it passes through. However, Geiger and Marsden’s observations of alpha-ray scattering indicate that some of the alpha particles must be deflected by more than a right angle in a single encounter […] A simple calculation based on the theory of probabilities shows that the chance of an alpha particle being deflected by more than 90° is infinitely small.
Rutherford then showed that if he used J.J. Thomsom’s model, it was impossible that in a single encounter (it should be noted that Rutherford avoided using the word shock, as this was unique to mechanics and not to electric field interaction, which was what was thought, including by himself, to be the case) the alpha particle would bounce back as seen in the experiment.

What did Rutherford propose? That the atom consisted of a nucleus concentrated at about \(10^{-12}\) cm surrounded by a sphere of electrons of radius \(10^{-8}\) cm. To demonstrate the adequacy of his model Rutherford derived a formula relating the fraction of the total number of particles that are deflected by an angle greater than \(\theta\), something that should in principle be experimentally measurable. What happened next is told by his then assistant, Hans Geiger:
One day (in 1911) Rutherford, clearly in the best of spirits, came to my room and told me that he now knew what the atom looked like and how to explain the great deviations of the alpha particles. That same day I began to check the relation which Rutherford expected to exist between the number of particles diffused and the angle of diffusion.
On 11 April 1911, barely a month after the presentation of his model at the Manchester Literary and Philosophical Society, Rutherford wrote to his colleague Bertram Borden Boltwood that Geiger and Marsden were working to prove the veracity of his formulae, something they achieved two years later, in 1913. So, it seemed that the first secrets of the atom were being unlocked, but…
Yes, dear reader, another one of those “hated” buts. We mentioned earlier that one of the great theoretical drawbacks of J.J. Thompson’s model was stability. Well, all the physics on which Rutherford’s model was based was the classical physics of Newton (mechanics) and Maxwell (electromagnetism), and it was well known that these theories predicted that an electric charge in accelerated motion, like the electron in Rutherford’s model, should radiate energy and therefore move in an orbit that would end up falling into the nucleus, something that also happened in a record time of the order of \(10^{-10}\) seconds. Once again mathematics, that indispensable part of the scientific method, dashed the hopes of physicists to decipher the mystery of atomic structure. Curiously enough, Rutherford himself was aware of this problem, and he avoided the issue at the end of his 1911 paper:
The question of the stability of the proposed atom need not be considered at this stage, since this will obviously depend on the internal structure of the atom and the motion of the charged constituent parts.
One is compelled to smile when reading this. But you have to forgive good old Ernest, because understanding the atom, and the whole microscopic world, required a new Physics, because classical Physics was unable to answer these kinds of questions. We saw this in the case of the radiation of a black body, and it was not going to be different in this case. We would need the recent Quantum Physics of Planck, Einstein and so on. But we will tell you about that in future posts.
Learn more:
José Manuel Sánchez Ron, Historia de la física cuántica: I. El período fundacional (1860-1926), Drakontos, 2001.
You can find out more about Rutherford’s life and work on the web at: https://history.aip.org/history/exhibits/rutherford/

Leave a Reply