Over the course of several posts we have chronicled the birth of quantum theory, the theory that attempts to describe the microscopic world, the micro-world beyond the reach of our sight. Although it was Max Planck who introduced the famous quanta in 1900, it was not until Einstein’s work (1905-1909) and Compton’s experiments (1922-1923) that the quanta, at least in the case of light, were accepted by the rest of physicists (as we described here). From that moment on, the number of physicists interested in quantum theory and its mysteries began to grow exponentially. In this post we are going to tell the story of one of them, the Frenchman Louis de Broglie and his Wave Mechanics.

Louis-Victor Pierre Raymond de Broglie, known as Louis de Broglie, was born in 1892 into a French noble family (his father was the 5th Duke de Broglie, a title inherited by his eldest son, Maurice, and after his death, Louis). Louis finished high school in 1910 and enrolled at the University to study History and Law in order to become a high-ranking civil servant. However, and probably influenced by his older brother Maurice, who was by then already a well-known experimental physicist, he became interested in science and in 1911 moved to the Faculty of Science. Maurice de Broglie had been, together with Paul Langevin (another famous French physicist), the editor of the proceedings of the First Solvay Conference (the history of the Solvay Conferences deserves a separate post) which took place in Brussels at the end of 1911 and which was devoted to the recently appeared “Theory of radiation and quanta”. This congress brought together some of the most famous physicists of the time, including Einstein, Planck, Sommerfeld, Marie Curie, Poincairé, among others. Louis read these notes, which had an enormous influence on the young student. He himself recounted this in 1953:
“With the passion of my age, I took an enthusiastic interest in the problems that had been discussed, and I promised myself to devote all my efforts to gaining an understanding of the mysterious quanta, which Max Planck had introduced ten years earlier into theoretical physics, but whose profound significance had not yet been grasped.”

In 1913 de Broglie obtained his degree in Science and in the same year he joined the French Army Corps of Engineers to do his compulsory military service. On the recommendation of his brother Maurice, Louis became involved in research related to wireless telegraphy where, in addition to his brother, he collaborated with Léon Brilloun, another renowned French physicist. While working in the Corps of Engineers, he was surprised by the First World War, which kept him in the army until the end of the war in August 1919. Although de Broglie’s work during the war was quite successful, Louis was not happy because, as his brother Maurice later recounted, he was forced to abandon his studies and research into the fundamental problems of quantum theory and relativity, which he was only able to resume with great effort many years later.
After the war, Louis de Broglie attended several advanced physics courses at the University and worked in his brother Maurice’s laboratory. Here, they were interested in problems related to X-ray spectroscopy (which we covered in a previous post), the photoelectric effect, the atomic structure of heavy atoms, etc. Although de Broglie published a series of interesting papers between 1920 and 1922, it cannot be said that they were very relevant contributions; they were good articles but not revolutionary. But that was soon to change, because during those years de Broglie would forge an idea that would cause a breakthrough. After many discussions with his brother Maurice and Brilloun, Louis hatched the idea that particles could behave, under certain conditions, like waves. This is how de Broglie put it in 1953:
These long debates with my brother were very useful for me, because they made me think deeply about the need to always have the wave and particle (corpuscle) points of view together.
Léon Brilloun recalled years later that de Broglie, in 1921-22, sitting in his laboratory observing the results of some experiments on particle emission from radioactive sources, remarked to him: “Well, all this must be very similar. Either it’s all waves or it’s all particles”. Since Einstein had already explored the particle path (the light quanta), all that remained to be explored was the other possibility: that everything was waves, and that is what de Broglie did in 1923. In that year, as Brilloun tells us, de Broglie discovered the relationship between the momentum and the wavelength of a particle in motion.
What was de Broglie’s discovery? Einstein had established in his 1905 theory of the photoelectric effect that a light quantum of frequency \(\omega\) had an energy \(E=h\omega\), where \(h\) is Planck’s constant (something that was verified by the famed American physicist Robert Milikan). A few years later, in 1922, Compton showed experimentally that light quanta also had a linear momentum equal to \(p=h\omega/c=h/\lambda\), i.e. light quanta could be seen as particles with a given energy and linear momentum. This same result (i.e. that all electromagnetic radiation could behave as particles with a given energy and a given linear momentum, i.e. the corpuscular theory of light) had been arrived at by de Broglie in 1922, but by a totally different route. So de Broglie wondered what if we were now to consider that every particle in motion with momentum \(p=mv\) behaved as a wave whose wavelength \(\lambda\) was given by the same expression as that of the quanta of light? In his own words:
When I began to formulate, in the period 1922-23, the basic ideas of wave mechanics, I intended to extend to all particles the wave-particle coexistence that Einstein had discovered was present in the case of light.
Moving from the case of a quantum of light to that of a particle (an electron, for example) took de Broglie about a year. The results were published in 1923 in a series of three articles in the French journal Comptes rendus, which he further developed in his 1924 doctoral thesis. This is how he described it 40 years later:
As in my conversations with my brother, we always came to the conclusion that, in the case of X-rays, one had waves and corpuscles [both], suddenly – I cannot give the exact date of when it happened, but it was certainly in the course of the summer of 1923 – I had the idea that one had to extend this duality to material particles, especially to electrons. […]
and after a non-trivial and non-intuitive reasoning that connected theories of classical mechanics (Newtonian mechanics), geometrical optics, quantum and wave phenomena, he concluded:
I then said to myself that there must be a wave property associated with quantum phenomena, and I wrote three notes for Comptes Rendus in September and early October 1923, in which I tried to formulate these ideas with precision. These three notes together contain the essential ideas which then went into my thesis, which I wrote later.
What would soon become known as wave mechanics was born.
After the publication of these three papers, de Broglie embarked on the preparation of his doctoral thesis, which he finished writing in the summer of 1924 and submitted on 25 November 1924. In it de Broglie completed his results published in 1923 and attempted to bring order to the apparent chaos of quantum physics at the time. De Broglie took for granted the existence of Einstein’s light quanta and that they had the property of behaving as waves and particles at the same time: the wave-corpuscle duality of electromagnetic radiation (discussed here). Now, to answer the question posed in 1911 by Poincairé, Can we construct an adequate dynamics for the quanta? de Broglie took the opposite path to Einstein: to each material particle in motion he associated a wave with a wavelength perfectly defined by the formula
\(\lambda=\displaystyle\frac{h}{p},\)
where \(p=mv\) is the linear momentum of the particle. On the basis of this hypothesis, the wave-corpuscle duality of both particles and radiation (what we now call the wave-particle duality of matter), de Broglie could reproduce and explain practically all the results obtained up to that time in quantum theory, but …
Yes, dear reader, another one of those “buts”: what was the physical interpretation of his theory? De Broglie was aware of this problem and wrote so in the conclusions of his 1924 thesis:
Therefore, the present theory should be regarded more as an outline whose physical content is not fully defined than as a coherent doctrine that is definitely established.
As mentioned above, de Broglie defended his thesis on 25 November 1924. The examination panel was composed of great figures of French science: the physicists Jean Perrin (who was the president of the commission), Charles Victor Mauguin and Paul Langevin, and the mathematician Élie Cartan. According to the board, the ideas of the thesis were elegantly defended and the defence was quite good, however, some were not very convinced of the veracity of the ideas. For example, Mauguin acknowledged 30 years later that:
At the time of the defence of the thesis, I did not believe in the physical reality of waves associated with particles of matter. Rather, I considered them (waves) as very interesting imaginary objects, which allowed, for the first time, to avoid the completely empirical character of the rules of quantification, providing the latter with a simple, almost familiar interpretation, analogous to the laws of vibrating strings.

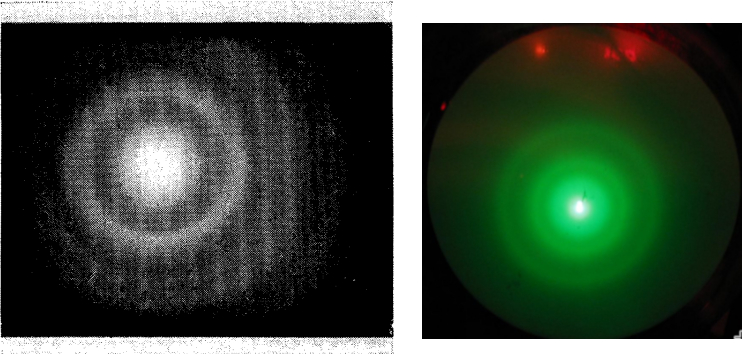
Something similar happened to Perrin. He could understand that during the interaction of electrons with other objects, X-rays of a certain frequency could be produced, i.e. that the particles could be transformed into waves, but whether the particles themselves were waves was another matter, so he asked de Broglie during the defence if he knew of any experimental way of verifying his ideas. De Broglie did not know of any experiments, but suggested that surely experiments could be done where very small particles (especially electrons) pass through very narrow slits. If indeed the particles (electrons) behaved like waves then a diffraction pattern similar to the diffraction of light would be seen. In fact, after his defence, he tried to convince Alexandre Dauvillier, one of the physicists in his brother Maurice’s laboratory, to perform such an experiment, but to Dauvillier’s disgrace he did not succeed, as we shall see later.
Paul Langevin’s opinion was quite different. Langevin found the thesis tremendously interesting, so much so that he asked de Broglie for permission to send a copy to Einstein, undoubtedly the greatest expert on the subject at the time. De Broglie himself recalled it with great satisfaction years later:
One day, Mr Langevin wrote to me, or phoned me, and said, “I spoke to Einstein about your thesis and he was interested; he would like to have a copy, do you have a typed one?” I said, “Yes, fortunately, I had three copies made and I have one.” Well, I sent him a copy, which he sent to Einstein.
Einstein carefully studied the thesis and was impressed. So much so that in a letter to Langevin dated 16 December Einsten wrote to him
The article [thesis] of de Broglie impressed me very much. He has lifted a corner of the great veil [Er hat einen Zipfel des grossen Schleiers gelüftet]. In a recent article I arrive at results which seem to support his own. Please convey to him my great respect and moral support when you see him. I want to present his ideas at our colloquium.
That same day Einstein writes to Hendrik A. Lorentz
The younger brother of [Maurice] De Broglie (whom we know) has made a very interesting attempt to interpret the Bohr-Sommerfeld quantization rules. I think it is the first ray of weak light to illuminate these rules, the worst of our physical puzzles. I have also discovered something that supports his construction.
Einstein’s support, as in Bose’s case, was providential. First, he convinced Langevin of the relevance of de Broglie’s work. But Einstein did much more. As J. Mehra and H. Rechenberg tell it in their encyclopaedic work “The Historical Development of Quantum Theory”, he did more than that:
He [Einstein] advocated De Broglie’s ideas in his second communication to the Prussian Academy on the quantum theory of an ideal gas (Quantentheorie des einatomigen idealen Gases. 2. Abhandlung, Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin), Physikalisch-mathematische Klasse, 1925, 3-14); he showed that the phase wave hypothesis [wave-particle duality] supported the quantum statistics of S. N. Bose and himself, thus providing further evidence of the correctness of Louis de Broglie’s ideas. Einstein’s article served to familiarise many physicists outside France with de Broglie’s work.
And how does our story end? Was de Broglie right? Or, as Mauguin thought, was his idea a mere artifice? There could only be one way to solve this problem: to test de Broglie’s hypothesis experimentally. We have already seen that during the defence of his thesis de Broglie had suggested a possible experiment (electron diffraction) and so did Einstein in his paper on ideal gases mentioned above.

Well, it turned out that none of the protagonists of our story were aware of an experiment that had been carried out by two Americans, Clinton J. Davisson and his assistant C.H. Kunsman, the results of which they had published in 1923. Davisson and Kunsman had discovered that when they bombarded a platinum plate with electrons, the electrons diffused through the plate in such a way that they apparently showed a diffraction figure, which was rare at the time (remember that de Broglie’s work appeared only in 1923 and 1924). Although there were some theories (proposed by the German physicist Max Born, which we will discuss in some future post) that attempted to explain the phenomenon, no one had tried to develop them mathematically. The then young physicist Walter Maurice Elsasser learned of this work during a seminar in Göttingen, which Born was organising. Some time later, Elsasser came across Einstein’s articles in which the quantum theory of ideal gases (mentioned above) was developed and in which reference was made to de Broglie’s thesis. It turned out that there was a copy of de Broglie’s thesis in the Göttingen library (Born had apparently requested it and de Broglie had sent him a copy). After reading it, Elsasser wondered whether he could not explain Davisson and Kunsman’s result using de Broglie’s theory. What a surprise it must have been when he discovered that the math worked out perfectly. After publishing a small note about it, Elsasser convinced his tutor in Göttingen, the prestigious experimental physicist James Franck, to let him use his laboratory to try to perform the experiment that would confirm his calculations and thus the veracity of de Broglie’s wave theory. Unfortunately, he only half succeeded. This is how he told the story years later:
I tried for two or three months to design an experiment to find these things [electron diffraction]. Franck told me that I could have access to his lab and so on, but I couldn’t ask any of his more experienced collaborators to leave their work to help me, which is what I had asked [Franck] to do. So after thinking for three months I gave up because this [designing and performing the experiment] is a very difficult job for a 21-year-old student with no experience.
What Elsasser failed to achieve in Göttingen was achieved a little over a year later by Davisson himself, this time with the help of his new collaborator Lester Haibert Germer and two English physicists, George P. Thomson and Alexander Reid. Both teams discovered experimentally, and without a shadow of a doubt, the wave facet of electrons, something that was well worth a Nobel Prize in Physics, which was finally awarded to Davisson and Thomson in 1937 “for their experimental discovery of the diffraction of electrons by crystals”. Louis de Broglie had received it nine years earlier, in 1929 for “his discovery of the wave nature of electrons“. The consequences of these “imaginary waves“, which were not such, were not long in coming, but we will tell you about that another time.
Learn more:
[1] J. Mehra y H. Rechenberg, The Historical Development of Quantum Theory, Vol 1. The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900-1925, 1982 Springer-Verlag New York Inc.
[2] José Manuel Sánchez Ron, Historia de la física cuántica: I. El período fundacional (1860-1926), Drakontos, 2001.

Me hace recordar mis años de Física, Físico-Químixa y Técnicas Instrunentales en la Facultad de Farmacia de Santiago de C. He disfrutado con su lectura y tomo nota del resto de entradas.