Solución: El reloj con dos minuteros

A continuación mostramos la solución al Divertimento El reloj con dos minuteros.

Gracias a Juan Luis Varona por la solución que ha aportado.

Divertimento:

Un relojero coloca dos agujas idénticas como horario y minutero en un reloj. Suponiendo que cualquiera puede dar la hora observando el cielo con un error inferior a seis horas, ¿cuál es el error máximo que podemos cometer al dar la hora con ese reloj?

Solución:

Denotemos por \(x\) e \(y\) a la posición de las agujas, con \(0 \leq x,y < 12\).
El minutero proporciona una información redundante, pues si \(\eta\) denota al minutero y \(\xi\) a la aguja horaria, tenemos que
$$
\eta – 12\{ \xi \}=0,
$$
donde \(\{\xi\}\) es la parte fraccionaria de \(\xi\).
Así, tenemos uno de los siguientes casos:

1. \(y – 12\{x\}\neq 0\) y \(x – 12\{y\}=0\). En este caso, la aguja \(y\) es horaria, y podemos determinar la hora exactamente.
2. \(y – 12\{x\}=0\) y \(x – 12\{y\}\neq 0\). Este caso es simétrico al anterior.
3. \(y – 12\{x\}=0\) y \(x – 12\{y\}= 0\). En este caso el reloj no determina unívocamente la hora.
   Las ecuaciones \(y – 12\{x\}=0\) y \(x – 12\{y\}= 0\) se corresponden con 24 rectas de la forma
   $$\begin{split} & y  =12(x-n), \qquad n \leq x < n+1, \qquad 0 \leq n < 11 \\
   &x  =12(y-m), \qquad m \leq y < m+1, \qquad 0 \leq m < 11,\end{split}$$
   que se cortan en los 143 puntos del retículo:
   

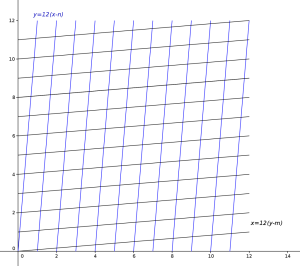
   Estos puntos se corresponden con la solución del sistema de ecuaciones $$\begin{cases} y =12(x-n) \\x=12(y-m), \end{cases}$$ que viene dado por la pareja de valores $$x=\frac{12}{143}(m+12n) \qquad y=\frac{12}{143}(n+12m).$$

Por tanto, el error máximo que podemos cometer al estimar la hora es
$$|x-y|=\frac{12}{143}|11m-11n| = \frac{12}{13}|n-m| = \frac{12}{13}k, \qquad k=1,\ldots,11.$$
Si además suponemos que el error es inferior a seis horas, el valor máximo se obtiene para \(k=6\),
es decir,
$$
|x-y| \leq \frac{72}{13}
$$
horas, que son 5 horas, 32 minutos y 18 y 6/13 partes de segundo.