I mean for mathematics. I have been reading arXiv entries related to my activity on a daily basis for many years. This year I have noticed an explosion of articles. Confinement has made mathematicians work like never before. This is not a novelty, it is said that Newton, retired in the countryside during a pandemic, conceived Calculus and Gravitation. André Weil in prison as an objector during the Second World War wrote to his wife:
My mathematics work is proceeding beyond my wildest hopes, and I am even a bit worried — if it’s only in prison that I work so well, will I have to arrange to spend two or three months locked up every year?
He even thought of writing to the authorities to recommend the imprisonment of mathematicians for a few months every year for the good of science. And we cannot forget other cases such as that of Bloch about whom I have recently written an article.
We should not get the idea that mathematicians are a bunch of lunatics immersed in their calculations. No, mathematics is very much a social activity, and the advancement of mathematics has a lot to do with travelling and meeting other mathematicians (although it may sound peculiar for me to say so). What is true is that mathematical creativity requires great concentration and tranquillity. You can’t constantly ask a mathematician for papers, to fill in applications, grants, projects, six-year periods, management activity. All this kills creativity. Nor can we ask them for a project of what they are going to do in the next few years. Creativity does not allow for such “projects”. If money is to be distributed, it must be based on what has already been done. Interesting projects, the most ambitious ones, cannot be included in these “projects” that ask for publications. If you try something really interesting, it is easy to fail. This encourages not creativity, but mediocrity, publishing a lot without making any progress.
Perhaps Bloch was so well off: table set every day, no obligations other than self-imposed study and research, isolated place to work without interruption, free from all paperwork, that he thought it better to pretend to be a fool than to do the foolish thing of ending his stay by appearing to be sane.
In this post we will discuss some of the results on which I base my assertion of the explosion of creativity. I will not discuss the topics in the usual depth, but only indicate each contribution, selecting a few out of many candidates. I will not include results that have already been discussed in my previous posts on this blog.
Orbit for a spy satellite
The problem was proposed by V. A. Zalgaller in 1996: what is the minimum length of a closed curve external to the unit sphere and such that its convex envelope contains the sphere?
The problem is equivalent to finding the curve of minimum length, external to the sphere and such that any point on the sphere \(A\) is visible from some point on the curve \(B\), that is, \(AB\) only cuts the sphere at the point \(A\). Already Zalgaller suggests that the solution is formed by the union of 4 semi-circumferences of length \(\pi\) each.
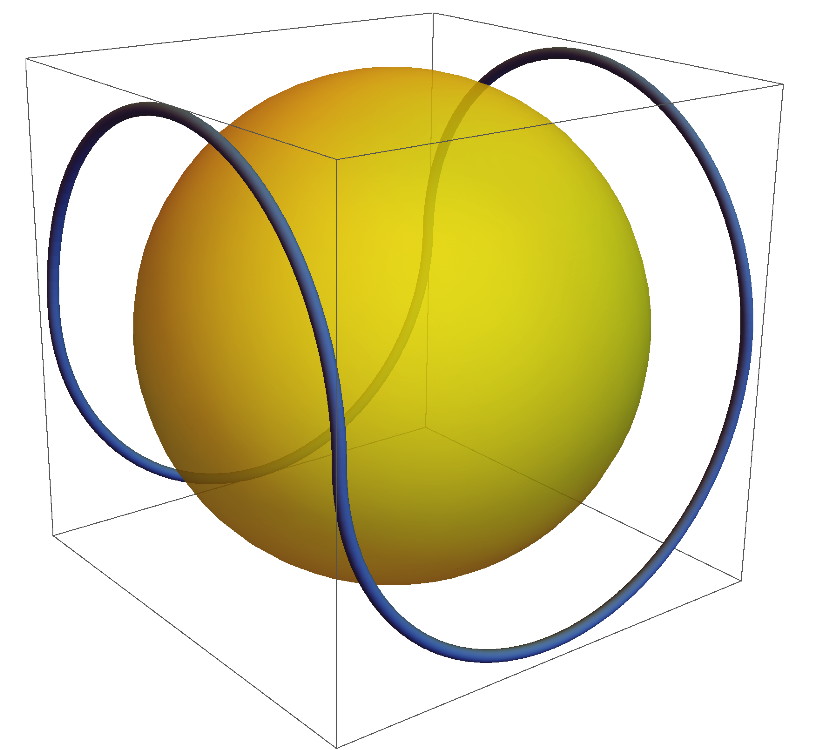
The problem was popularised when Joseph O’Rourke proposed it in June 2011 in MathOverflow.
On 29 October 2020 Mohammad Ghomi replied on MathOverflow with the solution he had uploaded earlier to arXiv. He proves together with James Wenk that the length of the curve is always \(\ge4\pi\) and equality is given only for the solution suggested by Zalgaller. Already in 2016 Mohammad Ghomi uploaded a partial solution to MathOverflow. So he has been working on the subject for some time, although he found the solution in 2020 during the pandemic. The solution uses ideas from Integral Geometry, Convex Analysis, Geometric Measure Theory, and Knot Geometry.
Our regular readers will recall that Joseph O’Rourke and Mohammad Ghomi were cited in our Dürer’s problem post.
The Conway and Jones problem (1976)
In 1976, in a very interesting article, Conway and Jones study equations of the kind of $$x\cos \Bigl(\frac{\pi y}{x^2+2}\Bigr)+(y^2+3x)\tan\Bigl(\frac{3\pi x y}{5y^2-7x}\Bigr)=1,$$ where there are rational functions with rational coefficients of the variables and trigonometric functions of angles that are products of \(\pi\) with rational functions –also with rational coefficients– of the variables. And solutions are sought with some integer variables \(x_j\in\mathbf{Z}\) and other rational variables \(y_k\in\mathbf{Q}\).
They prove that these equations are ultimately equivalent to ordinary diophantine equations without the intervention of trigonometric functions. And they add a method for solving the resulting equations using null sums of unit roots. They claim that their methods will possibly allow to find all tetrahedra with dihedral angles rational multiples of \(\pi\). An intermediate step in the attempt to determine all rectifiable tetrahedra, that is, those that can be dissected into polyhedra from which a cube can be formed.
Conway is among the victims of the covid, and that is why Kedlaya, Kolparov, Poonen and Rubinstein, dedicate to him the work we are discussing in which they determine all the tetrahedra with dihedral angles rational multiples of \(\pi\). The solution consists of 2 uniparametric families with dihedral angles \begin{align*}(\pi/2,\pi/2, \pi-2x, \pi/3, x, x), &\qquad x/\pi\in [1/6,1/2]\cap\mathbf{Q}\\(5\pi/6-x,\pi/6+x,2\pi/3-x,2\pi/3-x,x,x), &\qquad x/\pi\in[1/6,1/3]\cap\mathbf{Q}\end{align*} and 59 sporadic tetrahedra $$(\pi/4,\pi/3,\pi/4,\pi/3,\pi/2,4\pi/3), \dots (13\pi/60, 23\pi/60,\pi/4,7\pi/12,2\pi/5, 3\pi/5),\dots$$ that satisfy the conditions. Finding them all requires solving a polynomial with 105 monomials in roots of unity. All these tetrahedra are rectifiable. But as Conway and Jones state, we do not yet know all the rectifiable tetrahedra.
Monostable polyhedra
Conway and Guy (both deceased this year, the latter at the age of 103) conjectured in 1966 that a homogeneous tetrahedron is stable on at least two of its faces, but that there is a convex polyhedron that is stable on only one of its faces. These problems were solved positively in 1969. They called these polyhedra monostable and proposed three other related problems. The first question was whether there could exist a monostable polyhedron with an axis of symmetry with rotation \(2\pi/n\) with \(n>2\). The other question was whether a sphere could be approximated by monostable polyhedra. Both questions are answered in the affirmative in a paper by Zsolt Lángi uploaded to arXiv on 2 November 2020.
Apart from solving these problems, I was interested in the paper because of the information it provides about some polyhedra that surprised me:
(a) In dimension \(d\le 8\) no \(d\)-symplex (the analogue of the tetrahedron in dimension \(d\)) is monostable, but in dimension \(d=11\) there are monostable simplices. (R. Dawson et al.)
(b) Given a number \(r\) (think of a very large one), there exists a polyhedron of diameter \(1\) with the property that if we put it on a horizontal surface on a certain face, it rolls from this face to another and from this face to another,… until it reaches equilibrium at a distance \(>r\) from where it started. The authors of this version of the perpetual mobile Adrian Dimitrescu and Csaba D. Tóth title their article on this construction On the Cover of the Rolling Stone. I had a hard time finding it because if one searches the internet for the title, the song The Cover of “Rolling Stone” by Dr. Hook & The Medicine Show (1972) appears, which Dimitrescu and Tóth recognise as the inspiration for their title.
Moreover, such a polyhedron can be constructed in such a way that it has only one stable face and is as close as we want to a sphere.
Polynomial bijection \(p\colon \textbf{Q}\times\textbf{Q}\to\textbf{Q}\)
In 2010 user Z.H. asked on MathOverflow if there was any polynomial \(p(x,y)\) with rational coefficients that was a bijection between \(\mathbf{Q}\times\mathbf{Q}\) and \(\mathbf{Q}\). For a long time it has been the unanswered question that ranked first by number of points. The related question of whether there is a polynomial \(p\colon\mathbf{Q}\times\mathbf{Q}\to\mathbf{Q}\) that is injective was asked about 10 years earlier by Harvey Friedman and Don Zagier stated that the answer (to this second question) would possibly be positive and that for example \(x^7+3y^7\) could be an injective polynomial. The positive answer to the question of injectivity, under certain reasonable hypotheses, was given by Bjorn Poonen. The hypothesis he needed was the Bombieri-Lang conjecture.
In 2019 Terry Tao writes a blog post on the subject, in which he proposes a strategy for proving that there are no bijections, interestingly using the same hypothesis that Bjorn Poonen uses to prove that injectivities do exist. Tao comments that his knowledge of algebraic geometry is not enough to fill in the gaps in his reasoning but that he believes it could be a project for Polymath that will be successful in a short time. In January 2021 a paper has been uploaded to arXiv that proves that there are no bijections by assuming the Bombieri-Lang hypothesis and following the strategy suggested by Tao. But it is a paper that introduces a very complicated terminology for me.
The race to contradict Hedetniemi
Given a finite, loop-free graph \(G\), i.e., edges join distinct vertices, we can define its chromatic number, \(\chi(G)\), to be the smallest number \(n\) such that we can assign colours to the vertices of \(G\) such that two vertices joined by an edge have different colours and we do not use more than \(n\) colours. Hedetniemi’s conjecture states that \(\chi(G\times H)=\min (\chi(G), \chi(H))\). Here \(G\times H\) denotes the graph with pairing vertices of one vertex of \(G\) and one vertex of \(H\) and \((a,b)\text{—}(c,d)\) being an edge of \(G\times H\) if and only if \((a,c)\) is an edge of \(G\) and \((b,d)\) an edge of \(H\). The conjecture dates back to 1966. In 2019 Xuding Zhu published an article in Annals of Mathematics in which he proves the conjecture to be false. The paper is only 5 pages long but it is estimated that in his counterexample \(G\) has only \(4^{100}\) vertices but \(H\) has of order \(4^{10000}\). So the counterexample is finite by very little. Since then the pressure arises to give examples of \(\chi(G\times H)<\chi(G)\chi(H)\) more proportionate.
Shortly after the pandemic started, in April, Xuding Zhu uploaded a paper to arXiv with examples where the vertex numbers were \(|G|=912\) and \(|H|=553889\), and during the pandemic he kept working until he lowered these numbers to \(|G|=3403\) and \(|H|=10501\) almost in July. The paper is already published in the Journal of Combinatorial Theory B.
He is not the only one working on finding better graphs that contradict the conjecture. For example, Marcin Wrochna on Christmas Day (2020) uploaded another paper with an example where \(|G|=4686\) and \(|H|=30\). The race is still open.
Quantum Mechanics and Complexity
We come to the most surprising result of the year. A 206-page publication appeared in arXiv in September 2020. It deserves a separate entry, and I will only give here a brushstroke.
To explain it, we must remember some concepts:
The Halting Problem
This is the problem of deciding whether an algorithm will terminate or will enter an infinite loop. We know that it is unsolvable, that is, there is no algorithm \(A\) that, given a program \(P\), decides in finite time whether \(P\) will stop or enter a loop. This is so, it is an easy Turing theorem to prove.
(Note that we use the word problem in a special way, designating a collection of similar problems that we will call instances of the problem. Thus each program \(P\) is an instance of the Halting Problem).
Oracles
Suppose we are presented with an individual with superpowers. He tells us that he can solve the halting problem instantly. He is an Oracle (like the one at Delphi, or, since many say that God knows everything, he may be God himself :-)). So we assume that if we present the Oracle with a program, it tells us in a minimum amount of time whether \(P\) stops or loops. This oracle is pretty awesome, but we can think of other kinds of oracles with more credible superpowers, such as an oracle that tells us it can factor any number in polynomial time. Our goal is to decide whether we can give the oracle a certificate about its superpower.

MIP-type problems
Suppose we have an oracle for a superpower, which claims to solve the problem \(H\). If for each \(\varepsilon\), we are able to designate a set of questions to the Oracle, such that at the end of his answers we have (with probability \(1-\varepsilon\)) the certainty that he has the superpower, or else that he is a faker, we will say that the problem \(H\) is of type MIP.
To explain what I mean by this, I will consider a relatively modest Oracle. One that boasts of instantly deciding whether two graphs are isomorphic, that is, they are the same represented in different ways. What I do is find two graphs \(A\) and \(B\) that are sufficiently similar and have many vertices and edges. A graph is given as a set of vertices \(\{1,2,\dots, n\}\) and a set of edges \(\{(3,6),\dots, (k,l),\dots\}\).
From that moment on, I flip a coin, and if it is heads I make a copy \(C\) isomorphic to \(B\) obtained by permuting the vertices and changing the edges accordingly. If it is tails I do the same but copy the graph \(A\). I ask the oracle to tell me if \(A\) is isomorphic to \(C\) or not. If \(A\) and \(B\) were isomorphic the Oracle can only be right by chance with probability \(1/2\), but if \(A\) and \(B\) are not isomorphic the Oracle would always be right. Repeating this process, also with different \(A\) and \(B\), sometimes isomorphic and sometimes not, I can become convinced that the Oracle really has the superpower or that he is an impostor. So the problem of deciding whether two graphs are isomorphic is of type MIP.
This task of certifying Oracles has become more complicated over time. There is an advantage in having two Oracles with the same superpower if we can interrogate them separately. There is still a variant where both Oracles are allowed to make one or more measurements of a quantum system. Even if the Oracles are well separated, this gives them an advantage as the quantum systems can be entangled.
MIP*-type problems
We will say that a problem \(H\) is of type MIP* if we can decide whether two oracles have the superpower by interrogating them, but allowing them, being well separated, to share the measurements of a quantum system.
Well, what is shown in this article is that this class is equivalent to RE, the class of recursively enumerable problems, MIP*=RE. The Halting Problem is of the class RE. So we can certify two oracles claiming to be Oracles for the Halting Problem.
Already the result thus stated is very surprising: I would say that someone who has the superpower to solve the Halting problem has to be God. Well, this article resolves what questions we have to put to two gods with that superpower to convince us beyond reasonable doubt that they really do have that superpower. This is not mathematics, this is theology!
Learn more
Weil’s story can be seen in his biography, he considers his best result to be the one he proved in prison.
A. Weil, “The apprenticeship of a mathematician“, Birkhäuser, Basel, 1992.
But Weil enjoyed a cell for himself in benign conditions, much more complicated was the situation of Jean Leray, who developed the sheaf theory, among other results, during his 5-year stay in a concentration camp in Austria during World War II. This concentration camp became a university, classes were held, exams and degrees were given, 500 of the 5000 inmates obtained degrees after their liberation, with France recognising their studies. Leray, who acted as rector, wrote a treatise “Algebraic Topology taught in captivity”. There are many other examples of mathematicians in prison. Further information about Leray can be found in Leray in Edelbach.
Orbit for a spy satellite
The paper with the solution is in arXiv:
Mohammad Ghomi, James Wenk, Shortest closed curve to inspect a sphere, arXiv:2010.15204.
We can find useful information on the topic in MathOverflow.
The Conway and Jones problem
The problem was raised in the paper
J. H. Conway, A. J. Jones,Trigonometric diophantine equations (On vanishing sums of roots of unity), Acta Arith. 30 (1976), 229–240, DOI 10.4064/aa-30-3-229-240.
Marjorie Senechal is a mathematician who is also a brilliant speaker, and has a paper on the related problem as to which tetrahedra will fill the space:
Marjorie Senechal, Which tetrahedra fill space?, Math. Mag. 54 (1981), no. 5, 227–243, DOI 10.2307/2689983.
The article resolving the issue is available on arXiv:
K. S. Kedlaya, A. Kolpakov, B. Poonen, M. Rubinstein, Space vectors forming rational angles, arXiv:2011.14232, noviembre 2020.
Monostable polyhedra
The article we are commenting on can be found in arXiv:
Zsolt Lángi, A Solution to some problems of Conway and Guy on monostable polyhedra, arXiv:2008.02090, august 2020.
The article that builds the rolling stone is freely available online:
A. Dumitrescu and C.D. Tóth,On the cover of the rolling stone, Proceedings of the 31st Annual ACM-SIAM Symposium on Discrete Algorithms (2020), 2575-2586.
Polynomial bijection \(p\colon \textbf{Q}\times\textbf{Q}\to\textbf{Q}\)
One source of information is Tao’s blog where he sets out his strategy, another one is the old question in MathOverflow. The article that apparently solves the problem following Terry Tao’s strategy is
Giulio Bresciani, A higher dimensional Hilbert irreducibility theorem, arXiv:2101.01090.
The race to contradict Hedetniemi
There is a question on MathOverlow asking for information on reasonable counterexamples to the Hedetniemi conjecture. All the articles we have cited are available online: Shitov, Xuding Zu, and Wrochna.
Quantum Mechanics and Complexity
This is the only article I have commented on that actually appeared before the lockdown. But it has been growing during the confinement, the first version was uploaded to arXiv on 13 January 2020, it was a preprint of 165 pages, the second version was uploaded on 29 September 2020 and had grown to 206 pages. In any case, the repercussion that it generated justifies that we include it to give news of it, apart from the fact that we can dedicate a special article to it at a later date.
Zhengfeng Ji, Anand Natarajan, Thomas Vidick, John Wright, Henry Yuen, MIP*=RE, arXiv: 2001.04383 January-October 2020.
There is a great deal of information on this subject. I think I should at least cite Henry Yuen’s blog. In particular the posts: The shape of MIP* = RE and A visit from Alice and Bob.
But anyone searching the internet for “MIP*=RE” will find a lot of information, including three impressive videos of lectures by Henry Yuen at the Institute for Advanced Study in Princeton, the Fields Institute and the Simons Institute.
Denialists
As I write this I come across an article in the Financial Times, Where’s the spark? How lockdown caused a creativity crisis, unfortunately behind a wall, so I have not been able to read it. Of course, veryone’s views are colored by their own experience

Leave a Reply