The squaring of the circle

Problemas clásicos

How envious of the Greeks of classical times! Their gods posed mathematical problems, as when the Delphic oracle asked them to double the cubic altar to appease the plagues. We have here a plague of the devil and the bishops have done nothing but show their concern that “the offertory boxes are running empty”. 

Apart from the doubling of the cube, the Greeks also posed the squaring of the circle. These problems were solved many centuries later as has been described not long ago in this blog (Problemas matemáticos en tiempos de pandemia: la duplicación del cubo). Greek mathematicians assumed that they had to do the construction with ruler and compass. So understood, these problems were impossible, as Abel, Galois and Lindemann proved many centuries later.

But these problems took on a new and deeper life at the beginning of the 20th century thanks to the renewed vision of some mathematicians: Felix Hausdorff, Stefan Banach and Alfred Tarski, mainly. Perhaps Greek mathematicians were not ready to understand their gods.

The problem of measurement

At the beginning of the 20th century mathematicians considered the problem of defining the concepts of area and volume. In 1901 Lebesgue gives his definition. Very soon, in 1905, Vitali constructs his example of Lebesgue’s non-measurable set. So Lebesgue’s construction does not completely solve the problem. We want to define the area of any subset \(A\) of the plane \(m(A)\) in such a way that

• If \(A\) and \(B\) are disjoint sets \(m(A\cup B)=m(A)+m(B)\).
• If \(T\) is a movement of the plane and \(A\) is any set \(m(T(A))=m(A)\).
• If \(Q\) is a square of unit side \(m(Q)=1\)

If one thinks about it a little, one realises that these axioms must be sufficient to define the area. For example, it is easy to deduce that the points or segments must have zero area, since infinitely many disjoint copies fit inside \(Q\). One can deduce the measure of a triangle, from this the measure of any polygon, and with a little more work prove that the area of a circle of radius \(r\) is \(\pi r^2\), where \(\pi=4\int_0^1\sqrt{1-x^2}\,dx\). 

But all these reasonings start from the hypothesis that the function \(m\) exists. But this is exactly what Vitali had proved that Lebesgue had not achieved.

The doubling of the cube in the 20th century

In 1914 Hausdorff published his book Grundzüge der Mengenlehre, in which he demonstrates that the problem of volume measurement has no solution. For this he separates the surface of a sphere into four disjoint parts \(S^2=Q\cup A\cup B\cup C\), where \(Q\) is a countable set. He succeeds in proving that if there is a solution to the volume problem there is a solution to the measure problem on the sphere, and so \(Q\), being countable, must have zero measure. Hausdorff constructs two rotations of the sphere: one \(g\) of 120 degrees around an axis passing through the centre of the sphere and such that \(g(A)=B\), \(g(B)=C\) and \(g(C)=A\). Thus each of the three sets is one third of the sphere. But the second rotation \(h\), of 180 degrees, is such that \(h(A)=B\cup C\) and \(h(B\cup C)=A\). Then \(A\) and \(B\cup C\) are two halves of the sphere. \(A\) is both half and one third of the sphere.

Banach and Tarski, starting from Hausdorff’s construction, succeed in solving the cube doubling problem positively. They divide the unit cube \(Q_1\) and the double cube \(Q_2\) into parts \begin{align*} Q_1&=A_1\cup A_2\cup\cdots \cup A_N \\ Q_2&=B_1\cup B_2\cup\cdots\cup B_N.\end{align*} so that the \(A_j\) are disjoint two by two. The \(B_j\) are likewise disjoint two by two. And each part \(A_j\) by a movement of the space (a rotation and a translation) is transformed into the corresponding \(B_j\). So with the pieces \(A_j\) that compose the altar \(Q_1\) one can compose the double altar \(Q_2\) by simply moving the pieces \(A_j\) to their positions \(B_j\) in \(Q_2\).

Banach and Tarski achieve not only this, any two sets, which like the \(Q_i\) contain one ball and are contained in another, can be decomposed equally. This is what is called the Banach-Tarski paradox.

The problem of measurement in dimension 1 and 2

The Hausdorff construction and the Banach-Tarski theorem prove that the measurement problem has no solution in dimension 3, nor in any other dimension \(\ge3\).

The solution, this time positive, of the problem of measure in dimension 1 and 2, i.e. the definition of length on the straight line and area in the plane, was given by Banach, using all the techniques of functional analysis then emerging. There is one measure of length and another of area fulfilling the above conditions.

Tarski and the squaring of the circle

Tarski was interested in the definition of the concept of area. Banach had only proved the existence. Since in dimension 1 there is a solution of the measure problem, paradoxical decompositions of sets of different area are not possible.

On the contrary, Tarski wanted to prove that two flat sets \(A\) and \(B\) have the same area if and only if they are equivalent by finite decomposition. At least if the sets \(A\) and \(B\) are common flat figures.

The idea of decomposing two figures \(A\) and \(B\) into a finite number of parts \(A=A_1\cup A_2\cup\cdots\cup A_n\) and \(B=B_1\cup B_2\cup\cdots\cup B_n\) so that \(B_k\) is the result of a movement of \(A_k\) to prove that the two figures are equal, comes from antiquity. The classic Bolyai-Gerwien theorem tells us precisely that two polygons have the same area if and only if they can be decomposed into equal triangles two by two. In fact one of Hilbert’s problems raised the question of whether an analogous result was true for polyhedra.

\(A\) and \(B\) are equivalent by finite decomposition, \(A\equiv B\), if \(A=A_1\cup A_2\cup\cdots\cup A_n\) and \(B=B_1\cup B_2\cup\cdots\cup B_n\) can be decomposed so that the \(A_k\) and \(B_k\) are isometric. The difference with classical theorems, such as the Bolyai-Gerwien theorem, is that Tarski requires the \(A_k\) sets (and the \(B_k\) sets themselves) to be disjoint. In classical geometry, the edges of the figures were not taken into account. But Tarski’s figures have no edges and he required the \(A_k\) (and the \(B_k\)) parts to be disjoint.

Tarski succeeds in proving that two polygons have the same area if and only if they are equivalent by finite decomposition.

 

But Tarski was not satisfied with just polygons, he wanted to prove that any two figures \(A\) and \(B\) of classical geometry with the same area were equivalent by finite decomposition. When he failed to do so, he posed the problem of whether a disc and a square of the same area were equivalent by finite decomposition. This was in 1925 and is the revival of the classical problem of squaring the circle but now understood in a more basic way.

The solution of this problem is due to Miklós Laczkovich, first in 1990 he proves that the square and the circle are equivalent by finite decomposition, later in 1992 he extends his result by proving that two flat sets \(A\) and \(B\) with equal positive measure and with boundaries of dimension less than \(2\), are equivalent by finite decomposition, thus answering Tarski’s question positively and with great generality. The squaring of the circle is possible, understood in Tarski’s sense.

In his solution, Laczkovich manages to decompose the circle into \(10^{50}\) pieces which by translations alone compose the square. These parts might in principle not be Lebesgue measurable. Four years ago we wrote an entry, Squaring the circle, in which we explained the demonstration of the squaring of the circle with measurable pieces, a feat accomplished by the mathematicians L. Grabowski, A. Máthé and O. Pikhurko. All these constructions are more theoretical than practical. Today we tell of a new breakthrough in squaring the circle. One that we can really say is practical.  

All these constructions we have considered inherit something of the paradoxicality of the Banach-Tarski theorem, apart from the miracle of the loaves and fishes which is not documented, nobody expects to get two gold bars from one using the Banach and Tarski technique. The problem is that they are not constructive. What Andrew S. Mark and Spencer T. Unger achieve is squaring the circle with pieces that are Borel sets. This makes the pieces constructible and we can compute them. So much so that Mark and Unger have built figures, and even a film, with their solution.

First step: decomposition by means of Borel functions

In a previous step they construct a finite set of measurable Borel functions \(f_1\), …, \(f_N\) and corresponding translations \(a_1\), …, \(a_N\in\mathbf{R}^2\) such that $$\chi_S(x)=\sum_{k=1}^N f_k(x), \quad \chi_D(x)=\sum_{k=1}^n f_k(x+a_k),$$ where \(\chi_S(x)\) is the characteristic function of the square which is \(1\) if the point \(x\in S\) and \(0\) otherwise. \(\chi_D(x)\) is the characteristic function of the disk.

A useful technical trick is to consider the torus \(\mathbf{R}^2/\mathbf{Z}^2\) instead of the plane \(\mathbf{R}^2\). That is, we identify points in the plane whose coordinates differ in integers. So that in the translations what disappears on one side of the square appears on the opposite side.

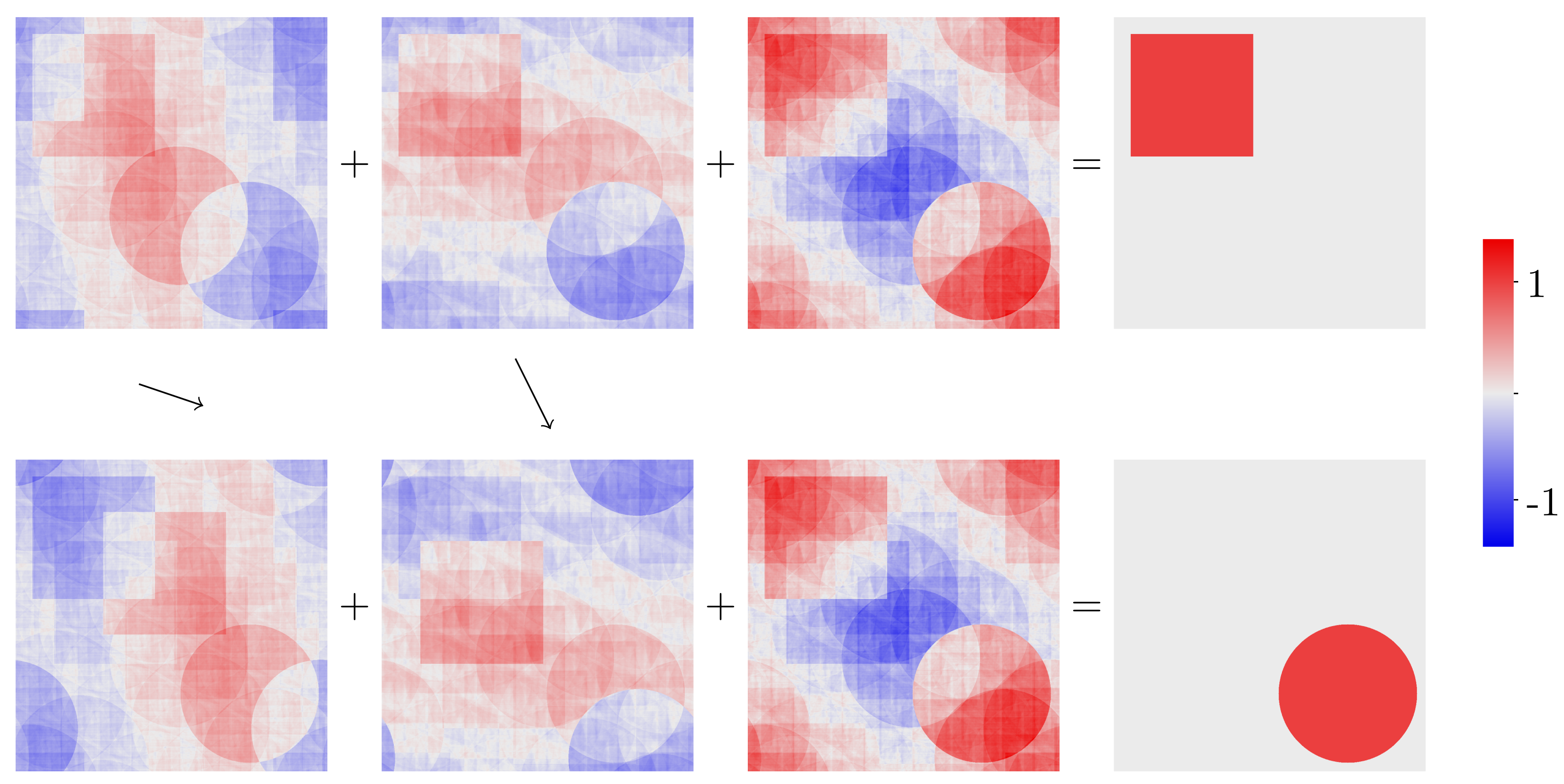
In the figure we see three bounded functions, representing their values by shades of colour. The three functions, represented in the upper line, add up to \(\chi_S\). Secondly, we see on the bottom line the three translated functions (represented in the same way as before), which this time add up to the characteristic function \(\chi_D\) of the disc. On Andrew Mark’s website we can see this figure, and also a larger one with a video in which we first see one of the functions moving and then the other in the process of converting the square into the disk.

These functions are calculated using the formula they give for constructing the function in their paper. This formula consists of taking a limit of averages of the function values \(\chi_S-\chi_D\) and their translated along translations of the type \(n_1 a_1+\cdots n_d a_d\) with \(a_j\) fixed translations and \(n_j\in\mathbf{Z}\). The theorem states that by properly taking \(a_j\) and \(d\) the process converges, but the figures have been obtained by forcing the value of \(d\) to be as small as possible and checking that with these values the averages were convergent.

This is only a first step, but they succeed in squaring the circle with Borel pieces. They obtain a decomposition of the square into 22 pieces that when translated make up the disc. They use 22 colours to represent the different pieces. I think that distinguishing the 22 pieces is difficult even for a person with normal eyesight, for a colour blind person like me it is a bit more difficult. I take this opportunity to say that with a red filter, looking alternatively with and without it, I manage to separate most of the pieces, in case any colour blind person wants to try it. Again, there is a larger version on Andrew Mark’s website.

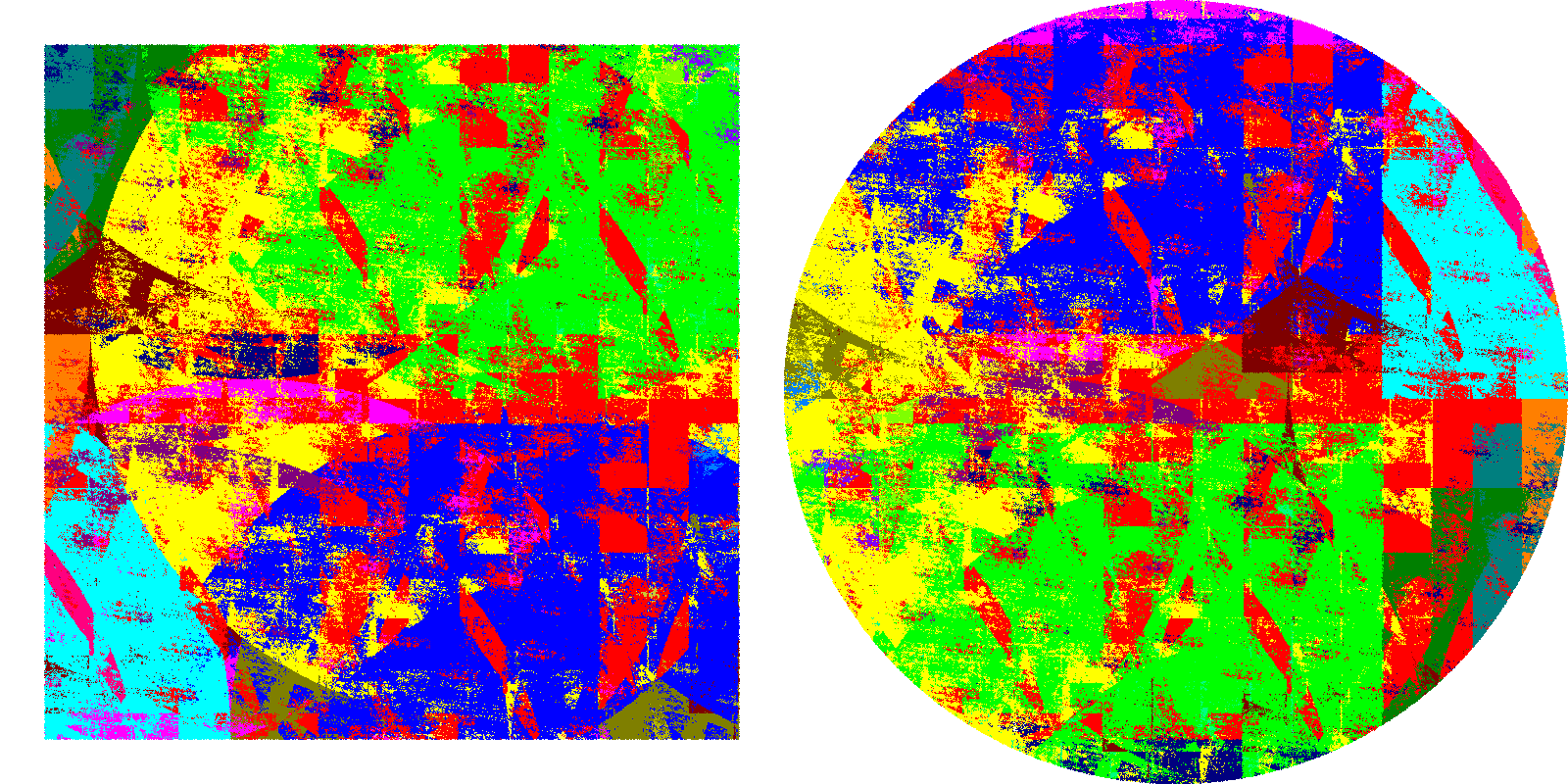
Someone might think it would be desirable to have simpler pieces, making it possible to make a puzzle and make some money out of the idea by selling it as a toy. But this is not possible, the one shown is likely to be the simplest solution. This was tried many years ago by Lester Dubins, Morris Hirsch and Jack Karush. They called two figures that could be transformed by pieces bounded by Jordan curves congruent with scissors. They proved that the disc is not scissor congruent to any convex figure other than its translated ones.

Learn more

The commented article is published in Annals of Mathematics, and can be downloaded from arXiv:

A. S. Mark, S. T. Unger, Borel circle squaring, Ann. of Math. 186 (2017) 581-605. arXiv:1612.05833.

There is a book on this and related issues that is highly recommended:

G. Tomkowicz, S. Wagon, The Banach Tarski Paradox, Second Ed., University Press, Cambridge, 2016.

Tarski’s life is very interesting. Information about him can be found at

A. B. Feferman and S. Feferman, Alfred Tarski. Life and Logic, Cambridge Univ. Press, 2004.

A. McFarland, J. McFarland, J. T. Smith, Alfred Tarski. Early Work in Poland – Geometry and Teaching, Birkhäuser, 2014.

S. Feferman, like many others, did his PhD with Tarski, the book must be friendly fire.

We have also commented on Laczkovich’s article and the one on congruence with scissors.

M. Laczkovich, Equidecomposability and discrepancy; a solution of Tarski’s circle-squaring problem}, J. Reine Angew. Math. 404 (1990), 77-117

L. Dubins, M. W. Hirsch, and J. Karush, Scissor congruence, Israel J. Math. 1 (1963), 239-247