En esta entrada analizaré algunos aspectos que surgen del análisis de la evolución de la COVID-19 mediante modelos epidemiológicos. En concreto, me voy a centrar en la segunda y tercera ola de la enfermedad en Andalucía (es decir, en el periodo comprendido entre el 12 de octubre de 2020 y el 20 de marzo de 2021), así como en los posibles efectos de la variante británica (B.1.1.7) del virus SARS-CoV-2. Para realizar este análisis, me basaré en algunos de los conceptos que aparecieron en mi primera entrada en este blog en la que tuve la osadía de realizar predicciones sobre la segunda ola; desgraciadamente, las predicciones fueron más optimistas que la realidad, pues en la mayoría de las ocasiones los modelos matemáticos son incapaces de prever el comportamiento humano, ya sea de políticos como de ciudadanos de a pie. En este punto, recomiendo al lector que eche un vistazo a dicha entrada si no lo ha hecho con anterioridad.
Segunda y tercera ola en Andalucía
En el análisis presentado en esta entrada he usado un modelo compartimental similar al de la entrada anterior, pero introduciendo una pequeña modificación: la inclusión de infectados presintomáticos. Para ello, me he basado en el modelo que hemos usado en un artículo recién publicado (aquí se puede descargar la versión preprint gratuita). No voy a hacer una descripción exhaustiva de lo que son modelos compartimentales, pero sí quiero explicar el funcionamiento del modelo que he usado para poder extraer conclusiones a partir del análisis de los datos de la segunda y la tercera ola en Andalucía. Para entender cómo funciona el modelo nos apoyaremos en el siguiente diagrama, en el que muestra los diferentes compartimentos en los que se divide la población y las conexiones que hay entre los mismos (dado los nombres de los compartimentos, podemos denominar a este modelo como SAPHIRED)
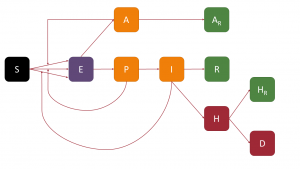
Así, una persona susceptible (S) de contagiarse, si entra en contacto con una persona infectada y esta última le transmite carga viral suficiente, pasaría a estar expuesta (E), es decir, contagiada pero sin posibilidad de contagiar durante el llamado periodo de latencia. Una vez transcurrido este periodo de tiempo, ocurrirá un paso fundamental en el proceso: la persona expuesta pasa a ser, o bien infectada asintomática (A), o bien infectada presintomática (P). En ambos casos, esa persona puede ya contagiar, pero, por otro lado, no presentará síntoma alguno; este hecho es el que hace a la COVID-19 en una enfermedad tan contagiosa (además de hacer dificultoso el análisis mediante modelos compartimentales).
Los individuos presintomáticos pasarán a ser infecciosos (I) sintomáticos tras el periodo preclínico, denominándose periodo de incubación al intervalo de tiempo que transcurre entre que una persona es contagiada hasta que muestra síntomas (es decir, la suma de los periodos de latencia y preclínico). Los infectados, tanto asintomáticos como sintómaticos, tras un periodo de infectividad, pasarán a un nuevo estado: los asintomáticos pasan al compartimento de asintomáticos recuperados (AR), mientras que los sintomáticos pasan, o bien a estar recuperados (R), o bien a estar hospitalizados (H). En estos estados los enfermos ya han dejado de infectar; para ello estamos asumiendo -algo no muy lejos de la realidad en la mayoría de los casos- que, cuando un enfermo es hospitalizado estará aislado de otros enfermos y el personal sanitario estará lo suficientemente protegido para no ser contagiado. Tras la hospitalización, los enfermos pueden recuperarse, pasando también al compartimento de hospitalizados recuperados (HR), o bien fallecer, pasando al compartimento de defunciones (D).
En el diagrama que se muestra a continuación, se resumen los diferentes periodos o tiempos característicos mencionados con anterioridad y su relación con el paso entre algunos compartimentos.
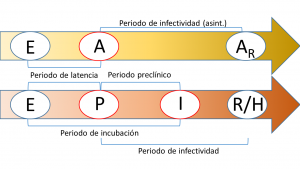
Uno de los principales problemas de los que adolece este tipo de modelos es la no identificabilidad de sus parámetros. Este problema, que no está presente en modelos compartimentales más simples como el SIR o el SEIR, consiste básicamente en que las soluciones a las ecuaciones que describen el modelo no dependen de los parámetros del modelo, sino de una combinación de los mismos y, en consecuencia, existe un conjunto infinito de parámetros que proporcionan exactamente las mismas predicciones. En el caso del modelo SAPHIRED, los únicos parámetros identificables (es decir, que no aparecen combinados con otros) son los tiempos característicos mencionados anteriormente (e ilustrados en la figura superior). Para mayor detalle, el lector puede consultar el siguiente artículo en el que abordamos este problema en un modelo similar (aquí se puede descargar la versión preprint gratuita). Otro problema al que nos enfrentamos y afecta principalmente a la tasa de transmisión (es decir, a la probabilidad de que una persona susceptible pase a estar expuesta mediante el contacto con un infectado), es la sensibilidad respecto a la variación de parámetros; en este caso, las tasas de transmisión tienen un intervalo de confianza muy amplio (en teoría, infinito) aunque, afortunadamente, las curvas de mejor ajuste presentan un intervalo de confianza razonable y se pueden realizar predicciones fiables (siempre que, claro está, la población no cambie sus hábitos).
Para hacer los ajustes con el modelo SAPHIRED hemos utilizado los datos suministrados por la Junta de Andalucía. Estos datos están agrupados por fecha de notificación al Ministerio de Sanidad, por lo que hay cierto retardo entre la fecha en la que realmente tienen lugar los diferentes eventos y la que usamos para hacer los ajustes; también tomamos la media para siete días en los datos para minimizar el denominado efecto fin de semana. Tomamos como «verdad absoluta» los datos relativos a las hospitalizaciones acumuladas y los fallecimientos acumulados. Así, el modelo «aprende» mediante el ajuste con estos compartimentos y, a partir de este aprendizaje, puede predecir qué les ocurre a los demás compartimentos o bien lo que ocurriría en el futuro si la población mantiene su comportamiento. En lo que respecta a los parámetros, hemos supuesto que todos son constantes excepto las tasas de transmisión (en nuestro caso, suponemos que hay dos, una debida al contacto entre individuos susceptibles y sintomáticos y otra para el contacto entre susceptibles y asintomáticos o presintomáticos). Hay que tener en cuenta que las tasas de transmisión, que dependen del número de contactos y de la carga viral, es el parámetro que se ve afectado por las diferentes medidas de contención de la epidemia, mientras que el resto de parámetros depende de las carácterísticas del virus. Así, hemos supuesto que las tasas de transmisión disminuyen a mediados de noviembre, aumentan a finales de diciembre y vuelven a disminuir a finales de enero (nótese que hay un retardo de un par de semanas con respecto a la fecha de aplicación de medidas en Andalucía). A finales de marzo habría una nueva subida de las tasas de transmisión, pero eso ya correspondería a la cuarta ola, la cual es bastante especial debido al proceso de vacunación y cuyo análisis lo abordaremos en una próxima entrada.
 En las figuras superiores se muestran los datos reportados para hospitalizaciones y fallecimientos, así como las las curvas de mejor ajuste. Los tiempos característicos obtenidos a partir de estos ajustes presentan la siguientes medianas:
En las figuras superiores se muestran los datos reportados para hospitalizaciones y fallecimientos, así como las las curvas de mejor ajuste. Los tiempos característicos obtenidos a partir de estos ajustes presentan la siguientes medianas:
- Periodo de latencia: 3,0 días
- Periodo preclínico: 2,5 días
- Periodo de infectividad (sintomáticos): 6,2 días
- Periodo de infectividad (asintomáticos): 6,1 días
Fijémonos que los infectados (con síntomas o sin ellos) tardarían 9 días desde el momento en el que son contagiados hasta que dejan de ser infecciosos. Este valor está de acuerdo con los 10 días de duración de las cuarentenas recomendados por las autoridades sanitarias.
De acuerdo a lo mencionado anteriormente, la curva correspondiente a los casos acumulados sólo puede ser predicha a partir de los parámetros obtenidos mediante aprendizaje por parte del modelo y comparada posteriormente con los datos suministrados por la Junta de Andalucía. Debemos tener en cuenta que en estos datos se encuentran todos los casos que han dado positivo en un test; es decir, que se incluyen individuos tanto sintomáticos como asintomáticos.
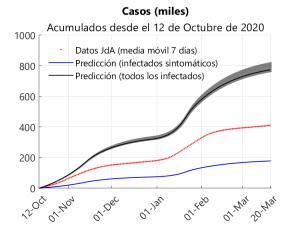
La figura superior muestra tres curvas para los casos acumulados desde el 12 de octubre: una para los datos suministrados por la Junta, otra para los casos sintomáticos (ahí se incluyen también los presintomáticos) y otra para los casos totales (la regiones sombreadas corresponden a los rangos intercuartílicos). Analizando los resultados mostrados en la gráfica y suponiendo que se han detectado todos los casos sintomáticos, se puede deducir que alrededor del 41% de los casos declarados serían sintomáticos y que se han detectado aproximadamente el 56% de los casos.
Variante británica: el caso de La Línea de la Concepción
Para finalizar la entrada, vamos a considerar el efecto que puede haber tenido la variante británica (B.1.1.7) en Andalucía. Teniendo en cuenta que esta variante ha convivido con otras en nuestra comunidad, debemos centrarnos en municipios en los que la variante británica haya sido la predominante durante la segunda/tercera ola. Ese ha sido el caso de La Línea de la Concepción, en la provincia de Cádiz. En este municipio, que está situado en la frontera con Gibraltar, alrededor de un 20% de sus 64.000 habitantes trabajan en este transfronterizo.
En el mes de diciembre se detectó por primera la variante B.1.1.7 en Gibraltar, lo que hizo que el territorio se confinara a finales de dicho mes, cerrando su frontera con España y limitando sus conexiones aéreas. En todo caso, esta variante debería estar presente al menos desde principios de noviembre; de hecho, el primer fallecimiento durante la pandemia en Gibraltar tuvo lugar el 11 de noviembre, y hasta esa fecha se habían detectaron 842 casos; cuatro meses después había 84 fallecidos y 4.256 casos, convirtiéndose en el «país» con mayor número de muertes por habitante en el mundo desde el comienzo de la pandemia (téngase en cuenta que la población de Gibraltar ronda los 33.700 habitantes). Una formidable campaña de vacunación (durante marzo se convirtió en el primer «país» en el que se alcanzaba el 70% de la población vacunada y, a fecha de 24 de abril está totalmente vacunada un 95% de la población) ha ayudado a que estos guarismos no fueran catastróficos. Estos datos dan una idea de la potencialmente alta propagación de la variante B.1.1.7. Como dato anecdótico, podemos destacar que a fecha de 24 de abril, Hungría ha desposeido a Gibraltar del deshonroso honor de ser el «país» con mayor índice de fallecimientos, ocupando el cuarto puesto tras Chequia y San Marino (España ocupa el puesto 21º, lo cual tiene bastante mérito tras haber ocupado el primer puesto durante la primera ola).
El hecho de que la población gibraltareña fuera vacunada durante esta oleada hace que no sea posible el estudio mediante el modelo SAPHIRED, ya que habría que añadir un compartimento adicional para los vacunados e incluir parámetros dependientes del ritmo de vacunación (que es, a su vez, bastante irregular). Por este motivo, decidimos estudiar a La Línea de la Concepción, pues dado el flujo tan alto de población entre este municipio y Gibraltar, la variante inglesa se hizo predominante en la localidad andaluza. Así, se pasa de haber acaecido 7 defunciones y 1.173 casos hasta el día 3 de diciembre a llegar a 105 defunciones y 5.233 casos el día 28 de marzo (o sea, el 6% de la población de La Línea se habría contagiado en este periodo). El hecho de que La Línea de la Concepción estuviera confinada perimetralmente a partir del 2 de Enero, permite que pueda estudiarse este municipio mediante un modelo compartimental, pues la entrada y salida de población fue mínima, de modo que La Línea puede considerarse como un sistema aislado. Así, hemos aplicado el modelo SAPHIRED al periodo comprendido entre el 10 de noviembre y el 14 de abril, suponiendo que todos los parámetros son constantes excepto las tasas de transmisión, que disminuirían a partir de mediados de enero. Para realizar el ajuste tomaremos los datos recopilados en Github por el investigador de la Universidad de Sevilla Francisco Rodríguez Sánchez, los cuales se basan a su vez en los publicados por la Junta de Andalucía. Solo hemos podido realizar el ajuste de las defunciones ya que la la Junta no ofrece los datos de hospitalizaciones en cada municipio.
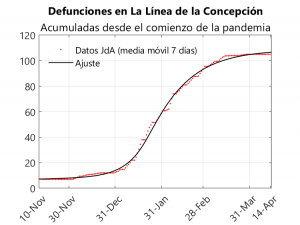
A partir de este ajuste obtenemos los siguientes valores para la mediana de los tiempos característicos (cfr. los datos obtenidos para toda Andalucía):
- Periodo de latencia: 2,6 días
- Periodo preclínico: 2,4 días
- Periodo de infectividad (sintomáticos): 5,9 días
- Periodo de infectividad (asintomáticos): 11,7 días
Nótese que el periodo de latencia es algo menor que en el caso de Andalucía; por otro lado, el periodo de infectividad de sintomáticos es similar al de Andalucía, aunque el periodo de infectividad para asintomáticos es sustancialmente mayor. Es decir, parece ser que la variante británica disminuye los periodos de latencia e incubación y aumenta el periodo de infectividad de los asintomáticos. Estos hechos contribuyen positivamente al aumento del poder contagioso de la variante. Estos cambios en los tiempos característicos pobrían ir acompañados de un incremento en las tasas de transmisión, hecho que no podemos saber con certeza a partir del ajuste con la curva de fallecimientos a causa de la falta de identificabilidad y/o la sensibilidad paramétrica mencionada en la sección correspondiente al análisis para Andalucía.
Para finalizar este análisis de la variante B.1.1.7, destacamos el estudio realizado entre jugadores, técnicos y empleados de varios clubes de la NBA (liga americana de baloncesto). Según este estudio, el tiempo que transcurre entre el contagio y la recuperación de los infectados por la variante británica es de 13,3 días en mediana (cfr. el valor de 14,3 días obtenidos para los asintomáticos con el modelo SAPHIRED). No obstante, los resultados de este estudio deben tomarse con mucha cautela, pues se ha realizado en una cohorte de 65 infectados, de los que en solo 7 casos se secuenció la variable británica. De hecho, este artículo se encuentra aún en proceso de revisión por pares.

Dejar una contestacion