We are happy being poor: Erdös-Faber-Lovász’s Conjecture

Combinatorial problems, as Number Theory ones, are easy to understand by everyone. They can even be more direct. Paul Erdös was very fond of combinatorial problems. He had a special gift for posing problems. Today we will discuss the near solution of one of his most famous problems, which he considered among his three favorite problems.

The problem arose in 1972 while Vance Faber, László Lovász and Paul Erdös were having tea. They were trying to find problems that would drive forward the theory of hypergraphs. As first step they propose a conjecture:

The \(n\) sets problem. Prove that if \(A_1 \), …, \(A_n \) are \(n \) sets, each of cardinal \(n \) and such that each intersection \(A_j \cap A_k \), with \(j\ne k\), contains at most one element, then there is a coloring of the union set \(\bigcup_ {k = 1} ^ n A_k \) with \(n \) colors so that each \(A_k \) has one element of each color.

They thought that the problem was a simple exercise and planned a meeting the next day to write down the best solution. None of them came up the next day with a solution.

Erdös was in the habit of awarding a cash prize to the first person who solved any of his problems. He set the value of this problem in 50 dollars. (With a good eye, even if you don’t have money, you can propose prizes. Like banks, that promise to save money, which actually they don’t have when you want it back.)

In 1981 Erdös wrote:

Faber, Lovász and I made this harmless looking conjecture at a party in Boulder Colorado in September 1972. Its difficulty was realised only slowly. I now offer 500 dollars for a proof or disproof. (Not long ago I only offered 50; the increase is not due to inflation but to the fact that I now think the problem is very difficult. Perhaps I am wrong.)

An example of the conjecture

I think that a good way to see what the problem is is to arrange the elements of the \(n \) sets \(A_k\), each with \(n \) elements on a board \(n \times n \). Each row represents a set. And every two rows share one element or none. Groping I have come to the following particular case: $$\begin{array}{|c|c|c|c|c|c|c|c|}\hline A & B & C & D & E & F & G & H \\\hline A & I & J & K & L & M & N & O\\\hline P & Q & J & R & E & S & T & Y\\\hline U & Q & V & K & W & X & G & Z\\\hline U & 1 & 2 & L & 3 & S & 4 & 8\\\hline B & M & Y & W & 11 & 1 & 10 & 6\\\hline D & N & T & X & 9 & 11 & 5 & 8\\\hline H & 7 & J & Z & 3 & 12 & 6 & 9\\\hline\end{array}$$ Thus, we see that rows 3 and 7 have the element \(T\) in common. In this case, the only rows that do not share an element are 1 and 5.

According to the conjecture we can color the elements with \(n \) colors so that each row has one element of each color (and naturally the common elements have the same color). We can turn this into a game. Let’s think that the elements in the \(k \)-th column are painted in color \(k \). Thus, each set (row) contains one element of each color. What happens is that this is not an allowed coloring because, for example, the element \(M\) in the second row is painted with the color 6 and the same element \(M \) in the 6-th row is painted with color 2.

But the elements of each row can be permuted without changing the problem since the \(A_j \) are unordered sets. So, the game consists of permuting the elements of each row, until all repeated elements are in the same column, as, for example, occurs with the \(A \) in the first and second rows. I leave the task to the reader.

The three faces of the problem

In order to be able to discuss the solution of the problem, we must familiarize ourselves with certain concepts,

We start with the concept of graph. A graph \(G = (V, E) \) is made up of a finite set \(V \) of vertices and a family \(E \) of edges that join them. We can think of edges as subsets \(\{a, b \} \subset V \) of two elements. We pay no attention at all to the structure of the vertices; \(V \) should be thought of as a set of points.

Mathematicians have long extended this structure to what is called a hypergraph.

A hypergraph \(H = (V, E) \) is composed of a finite set of vertices \(V \) and, in this case, \(E \) is a family of subsets \(A \subset V \) of \(V\) that we will call edges of the hypergraph.

A hypergraph is \(k \)-uniform if all edges have the same cardinal \(| A | = k \) (given a set \(A \), we designate by \(| A | \) its cardinal). The \(2 \)-uniform hypergraphs are ordinary graphs.

A hypergraph is linear if every two different edges \(A \) and \(B \) intersect at most at one point, that is, \(| A \cap B | \le 1 \). As with the lines of the plane, edges are either parallel or intersect at one point.

In a graph \(G = (V, E) \) a set of vertices \(Q \subset V \) is a clique if each pair \(a \ne b \in Q \) of elements of \(Q \) form an edge (\(\{a, b \} \in E \)) of \(G \).

If \(Q \) is a finite set we denote by \(C (Q) = (Q, Q ^ {(2)}) \) the complete graph that has \(Q \) as a set of vertices and its set of edges \(Q ^ {(2)} \) is maximal, that is, it is made up of all pairs \(\{a, b \} \) with \(a \ne b \) elements of \(Q \).

We will state three equivalent conjectures that are equivalent to the Erdös-Faber-Lovász conjecture.

Conjecture 1. Let \(V = \bigcup_ {j = 1} ^nA_j \) be a finite set, union of \(n \) subsets \(A_j \) each of cardinal \(| A_j | = n \) and such that for \(j \ne k \) we have \(| A_j \cap A_k | \le 1 \), then there is a function \(f \colon V \to \{1,2, \dots, n \} \) such that the image \(f (A_j) = \{1,2, \dots, n \} \) for all \(j \).

In the language of hypergraphs: Every linear and \(n\)-uniform hypergraph \(H = (V, E) \), admits a coloring of the vertices such that each color appears on each edge.

Conjecture 2. Let \(G = (V, E) \) be a graph such that there are \(n \) cliques \(Q_1 \), …, \(Q_n \) so that \(| Q_j | \le n \) for each \(j \), and such that for \(j \ne k \), we have \(| Q_j \cap Q_k | \le 1 \) and finally $$ E = \bigcup_ {j = 1}^ n Q_j ^ {(2)}. $$Then we can color the vertices of \(V \) with at most \(n \) colors and such that each edge \(\{a, b \} \in E \) has vertices of different colors

Finally, another equivalent version.

Conjecture 3. Let \(V \) be a set of cardinal \(n \) and \(E \) a family of subsets of \(V \) such that \(A \ne B \) in \(E \) implies \(| A \cap B | \le 1 \). Then there exists a coloration \(f \colon E \to \{1, \dots, n \} \) such that \(| A \cap B | = 1 \) implies \(f (A) \ne f (B) \).

In other words: Every linear hypergraph \(H \) with \(n \) vertices admits an edge coloring with no more than \(n \) colors. Of course, edge coloring requires that if \(| A \cap B | = 1 \), then \(f (A) \ne f (B) \).

The first conjecture is the \(n \) sets problem. It is not difficult to see that the three conjectures are equivalent. This what is known as the Erdös-Faber-Lovász conjecture.

For example, given sets \(A_j \) as in the \(n \) sets problem, we can consider a hypergraph \(H = (V, E) \) with set of vertices \(V = \{A_1, \dots, A_n \} \) and for each point \(a \in \bigcup_j A_j \) we consider an edge \(M_a = \{A_j \colon a \in A_j \} \). Applying Conjecture 3 to this hypergraph reduces the problem of \(n \) sets to Conjecture 3. From now on we will only consider Conjecture 3.

The authors and their theorem

A few months ago, in January of this year, an article has been uploaded to arXiv where its authors prove de following

Theorem. For every sufficiently large \(n\), every linear hypergraph \(H\) on \(n\) vertices has chromatic index at most \(n\).

The chromatic index \(\chi'(H)\) is the smallest number of colors needed to color the edges of \(H \) so that if \(A \cap B \ne \emptyset \), then \(A \) and \(B \) have different colors. Hence, they have proved the Erdös-Faber-Lovász Conjecture except for a finite number of cases.

Daniela Kühn and Deryk Osthus.

The authors are  professors Daniela Kühn and Deryk Osthus from the Combinatorics Group of the University of Birmingham, (although they come from German universities)  and three young people, Dong Yeap Kang, Tom Kelly and Abhishek Methuku, who are in their early postdoctoral studies, in the same group. Dong Yeap Kang is a Korean who defended his doctoral thesis in 2020 at the Advanced Institute of Science and Technology in Korea; Tom Kelly defended his doctoral thesis at the University of Waterloo in 2019 and Abhishek Methuku defended his doctoral thesis in 2019 in Budapest.

Don Yeap Kang, Tom Kelly and Abhishek Methuku

Tight cases of the conjecture

It is known that the conjecture is tight, in the sense that there are linear hypergraphs with \(n \) vertices \(H \) such that the chromatic index \(\chi ‘(H) = n \). There are essentially three examples:

Projective planes. For each finite field with \(q \) elements. The projective plane has \(q ^ 2 + q + 1 \) points and there are precisely \(q ^ 2 + q + 1 \) lines each with \(q + 1 \) points. We can thus form a hypergraph where the vertices are the points of the projective plane and the edges are the lines. Two different lines always intersect at one point, so the graph is linear. In a coloration, all the lines must have different colors since any two intersect. Therefore, the chromatic index is precisely the number of vertices \(q ^ 2 + q + 1 \).

Degenerated plane. Another extreme case occurs in the hypergraph $$H_n=(V=\{1,2,\dots, n\}, E=\{\{1,2\},\{1,3\},\dots, \{1,n\},\{2,3,\dots, n\}\}.$$ Obviously \(n \) colors are needed to color it.

Complete graph. The third and last extreme case is the complete graph \(K_n \) with \(n \) vertices and the \(\binom {n} {2} \) possible edges.

These three examples are important in the proof, because when a hypergraph is close to one of these examples we will have special difficulties in obtaining the coloration. In fact, one of the previous advances in the conjecture is Kahn’s theorem, which shows that the conjecture is asymptotically true since every linear hypergraph of \(n \) vertices satisfies \(\chi ‘(H) = n + o(n) \). Kahn suggested that for graphs far from the extremes the chromatic index would be less than \(n \). In the article that we are commenting, Kahn’s conjecture is proved by means of the following result

Theorem. For all \(\delta> 0 \) there is a \(\sigma> 0 \) such that for \(n \) large enough: If \(H \) is a linear hypergraph with \(n \) vertices such that

1. \(\Delta (H) \le (1- \delta) n \) and
2. at most \((1- \delta) n \) edges have size \((1 \pm \delta) \sqrt {n} \),

then \(\chi ‘(H) \le (1- \sigma) n \).

The degree of a vertex in a hypergraph is the number of edges where it is contained; \(\Delta (H) \) denotes the maximum degree of the vertexes. Thus, the first condition in the theorem eliminates the examples which are close to \(H_n \) and \(K_n \), and the second condition eliminates the examples which are close to the projective planes (recall that each line has \(q + 1 \) points, which is approximately the square root of \(n = q^ 2 + q + 1 \)).

The proof

Sometimes math proofs are like melodies; in this case it is more like a symphony. The ideal proof would be an algorithm that, given the linear hypergraph, determines the coloring of the edges. However, it is difficult to imagine an algorithm that would work in all cases. Rather, the proof consists on splitting the hypergraph into pieces, applying different algorithms to each piece, and then trusting that the pieces will somehow fit, and in case they don’t fit, modify something in the last part so that everything goes well.

Let’s imagine the problem solved. We will have the edges colored with \(n \) or less colors. Edges with the same color will be disjoint. This is what is called a matching: a set of disjoint edges. If we find a partition of the edges into \(n \) or less matchings, we will have the desired coloring. This is the reason why the proof searches for matchings, that is, sets of disjoint edges.

One of the authors, Abhishek, gave a lecture on February 16 at the seminar of the Alfréd Rényi Institute of Mathematics on the solution to the Conjecture. Among the attendees was László Lovász who congratulated Abhishek for the proof. I must thank Abhishek for the effort he made in describing the proof. I have taken the liberty of using his slides in this lecture to give the following short description of the proof.

Hierarchy of constants. Students take time to get used to demonstrations that contain the phrase “for every \(\varepsilon> 0 \) there is a \(\delta \dots \)”. With time we get used to it. This article has surprised me for the use (surely a routine to the authors) of the concept of hierarchy of constants. In the proof they use the following hierarchy: \begin{align*}0<&1/n_0\ll1/r_0\ll\xi\ll1/r_1\ll\beta\ll\kappa\ll\\ &\gamma_1\ll\varepsilon_1\ll\rho_1\ll\sigma\ll\delta\ll\gamma_2\ll\rho_2\ll\varepsilon_2\ll1\end{align*} that we must read from right to left. This is similar as saying: there is some \(0<\varepsilon_2 <1 \), and given this \(\varepsilon_2 \) there exists \(\rho_2 <\varepsilon_2 \). Then there is \(\gamma_2 <\rho_2 \) and, once all these constants are given, there is \(\delta <\gamma_2 \dots\).   I stop here, but the process continues until there is a natural number \(n_0 <\infty \) such that if \(H = (V, E) \) is a linear hypergraph with \(n \ge n_0 \) vertices, then we can color the edges \(E \) of \(H \) with no more than \(n \) colors.

These figures are from Abhishek’s notes. [/caption]

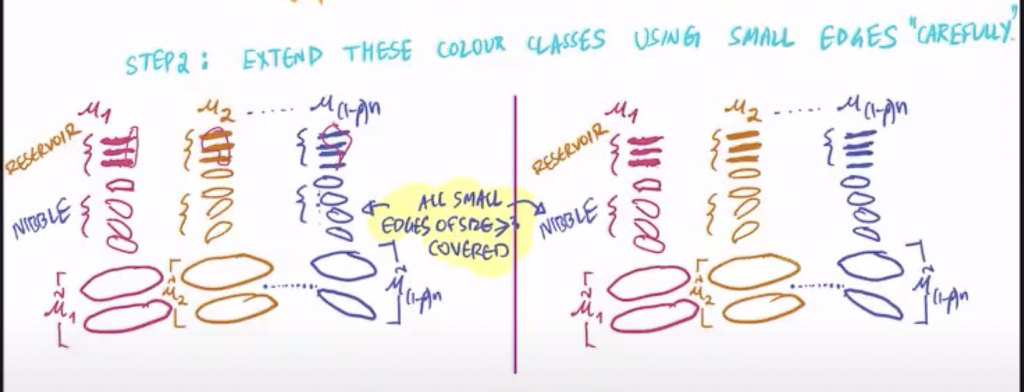
Firstly, one should organize the edges of \(H \) into three types, according to the number of edges that they contain: small, medium and large. The constants \(r_1 \) and \(r_0 \) are the ones that appear in the hierarchy of constants above.

The first step in the proof is to color the middle and large edges in such way that each color appears in few vertices. (This is not always possible, precisely when there are huge edges, and we are close to the degenerate plane. But let’s leave this case aside, because its solution is not the difficult part of the proof).

If we manage to pass the first step, two things can happen, (a) we have succeeded using few colors (say, using \(k \le (1- \rho) n \) colors, few compared to \(n \)); or (b) we needed practically all the colors.

Abhishek denotes by \(\widetilde{\mu_j}\) the matchings obtained from the large edges.

Now comes the main part of the construction. Step 2. We can see in the lower part of the figure [cases (a) and (b) separated, but essentially the same is done in both] the matchings, with different colors, formed with the large edges in the previous stage. Now we have to take almost all the small edges, those with cardinal \(\ge3 \), and extend the previous matchings with them.

This process is done via a random procedure called “Rödl nibble”, because it was introduced by Rödl in 1985 to solve another Erdös’ problem (the Erdös-Hanani conjecture).

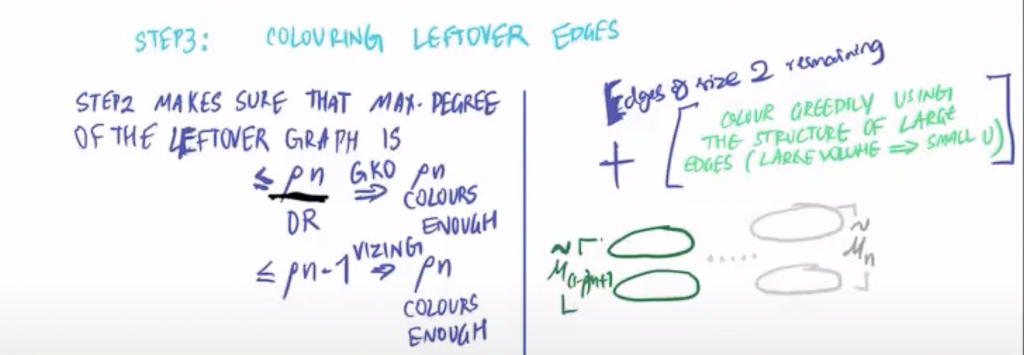
Once Step 2 is finished, we already have many colored edges. The remainder is formed by edges of cardinal 2, i.e., what remains is a graph in the ordinary sense and we can apply to it results from Graph Theory. In particular the Vizing theorem:

Theorem (Vizing). Every graph \(G\) with \(\Delta(G)\le D\) satisfies \(\chi'(G)\le D+1\). Moreover, if \(G\) contains at most two vertices of degree \(D\), then \(\chi'(G)\le D\).

With this, the edges of the remaining graph can be colored with \(\rho n \) colors and in case (a) we have finished, since these colors can be added with the \((1- \rho) n \) that we used in step 1 to color the entire graph with \(n \) colors.

In case (b) this is not enough. We are not telling the whole truth, but the structure of the graph in this case allows us to use colors from Step 1 in a compatible way. This case contains those cases in which the graph is close to the projective line.

Learn more

The paper we comment can be downloaded from arXiv:

Dong Yeap Kang, Tom Kelly, Daniela Kühn, Abhishek Methuku, Deryk Osthus, A proof of the Erdős-Faber-Lovász conjecture. arXiv:2101.04698 [math.CO] (2021).

There is an excellent webpage at quantamagazine written by Kelsey Houston-Edwards. Also Gil Kalai have also write in his  blog an entry about this.

Very interesting is the talk of  Abhishek at the seminar of the Alfréd Rényi Institute. At minute (1:36:21) you can see Lovász intervention:

László Lovász: Okay, I don’t actually have a question, a real question, but I just wanted to say how nice it is to see this really really hard old problem finally solved and I think I, yeah I must say that, so congratulations. Thank you for the nice talk as well.

Abhishek Methuku: Thank you very much.

And, do not miss the question of Katona:

Gyula Katona: Do you have some plans to collect the prize?

Abhishek M.: Well I have but, I don’t know, no, we don’t actually because uh as you know although he’s no more,  and Graham who manages the price is also no more, so, we are happy being poor.

Abhishek refers here to Erdös dying in 1996. After his death, Ron Graham distributed the prizes for Erdös problems, but Graham died in 2020.

There is another very similar talk  of Abishek, with same slides but a different audience and a different approach.

On the web such a prominent result has not gone unnoticed; many references can be found.