Kristin and Kirsten

This entry is dedicated to two great researchers: Kristin R. Swanson and Kirsten A. Morris. The former is a pioneer in the application of mathematics to the detection, understanding and therapy of tumours. The latter is a well-known specialist in the control of systems governed by partial differential equations, with particular applications to the behaviour of smart materials.

Let’s first talk about Kristin.

Kristin

She received her Master’s degree in Mathematical Biology in 1998 and defended her PhD Thesis in Mathematical Biology in 1999 in the University of Washington. After a postdoctoral fellowship in Mathematical Medicine at the University of California, San Francisco, she joined the University of Washington in 2000, with roles in Neuropathology and Applied Mathematics. In 2015 she joined the Mayo Clinic in Arizona as Professor and Deputy Chair of the Department of Neurological Surgery. There, hundreds of researchers dedicate their professional lives to reducing the effects of cancer. She also maintains permanent contact with Arizona State University and the Translational Genomics Institute.

Her research laboratory is a world leader in the field of mathematical neuro-oncology, generating data that support the practical application of personalised models to predict and optimise glioma treatment. Numerous institutions have funded her work over the years, including the James D. Murray Endowed Chair at the University of Washington.

As an example, let’s take a look at the fundamental ideas of one of her papers, which describes the evolution of a glioblastoma (a brain tumour).

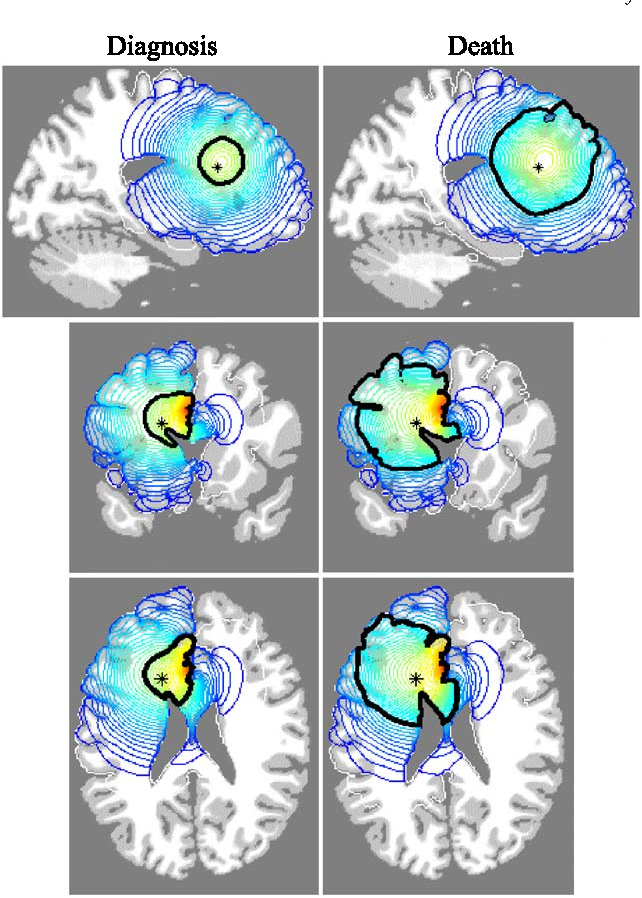
The whole thing is based on describing with appropriate formulae the following law: the rate of change of the tumour cell population coincides with the sum of the diffusion (or motility) of the cells plus the proliferation (or reproductivity) of the cells minus the death or deterioration due to therapy. If \(c = c(x,t)\) is a function that determines the density of cells at the point \(x\) at the instant \(t\), \(D\) and \(\rho\) are positive constants that allow us to quantify respectively their motility and reproductivity and \(G = G(t)\) determines the treatment, it is reasonable to suppose that \(c\) verifies the partial differential equation
$$
\frac{\partial c}{\partial t} – D \Delta c = \rho c – G(t)c,
$$

where, as usual, \(\Delta\) is the Laplace operator, that is, the sum of the second derivatives with respect to the components of \(x\). Knowing \(G\), the numerical resolution of this equation allows us to determine the evolution of the tumour.

In addition to her work in Biology and Mathematical Medicine, Kristin is author, together with other colleagues, of the book “The Mathematics of Marriage”, published in 2005, see [2].

This book attempts to present a theoretical explanation, based on mathematical models, of marital relationships, especially with regard to their stability and/or dissolution.

The tool chosen to model the related systems is difference equations.

Kirsten

Professor Kirsten Morris completed her PhD Thesis at the University of Waterloo and is currently a member of the Applied Mathematics Department at the University of Waterloo, with close links to the Mechanical & Mechatronics Engineering Department. She has also benefited several times from visiting professorial status at ICASE (NASA Langley), the Fields Institute and the Institute for Mathematics & Applications.

She is currently deputy director of the SIAM Control & Systems Theory Group and editor of several high-level scientific journals and collections.

Among other things, Kirsten Morris has contributed significantly to the analysis and control of systems associated with hysteresis phenomena. In intuitive terms, hysteresis can be said to be the tendency of a material to retain a property in the absence of the stimulus that generated it. For example, hysteresis occurs when, after magnetising a ferromagnet, the signal is retained even after removing the previously applied magnetic field. This behaviour allows the storage of information on a computer hard disk: the applied field induces a magnetisation, which is encoded appropriately. This coding remains in the absence of the field, and can be read later. Similar phenomena are also observed in many elastic materials subjected to prolonged stresses (indeed, the stress-strain curve that a rubber band follows when it stretches is different from the one it follows when it contracts).

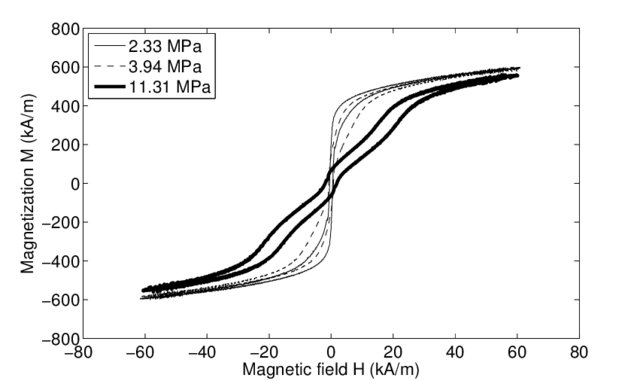
In hysteresis phenomena it is typical to find loops, such as the one in Figure 4. The idea pursued by Professor Morris is to exploit this behaviour to improve the performance of imposed controls and thus optimise (for example) data recording processes.

To learn more

1. Swanson K.R., Alvord Jr. E.C., Murray J.D., Virtual brain tumors (gliomas) enhance the reality of medical imaging and highlight inadequacies of current therapy. Br. J. Can. 2002; 86:14 – 8.

2. Gottman J.M., Murray J.D., Swanson C.C., Tyson R., Swanson K.R., The mathematics of marriage, dynamic nonlinear models, Bradford Books, MIT Press, 2005.

3. Jackson P.R., Juliano J., Hawkins-Daarud A., Rockne R.C., Swanson K.R., Patient-specific mathematical neuro-oncology: using a simple proliferation and invasion tumor model to inform clinical practice, Bull. Math. Biol. 2015; 77(5): 846-856, DOI: 10.1007/s11538-015-0067-7.

4. Valadkhan S., Morris K.A., Shum A., A new load-dependent hysteresis model for magnetostrictive materials, Smart Materials and Structures, October 2010, DOI: 10.1088/0964-1726/19/12/125003.

5. Morris, K.A., Control of systems governed by partial differential equations, IEEE Control Handbook Publisher, December 2010, DOI: 10.1201/b10384-79.

6. Morris K.A., What is hysteresis?, September 2011, Applied Mechanics Reviews 64(5): 1001, DOI: 10.1115/1.4007112.