Solution: Forgotten formula

We publish here the solution to the divertimento Forgotten formula.

The fun

A student taking an exam on the applications of Trigonometry is asked for the area of a trapezoid of which the two bases \(B\) and \(b\) are known, which are two integers, and the angles formed by the non-parallel sides with the larger base, 30º and 60º respectively. The student calculates the height \(h\) of the trapezoid, but does not remember the formula for the area of the trapezoid (which is not in the topic being examined) and does not know how to deduce this formula, hesitating between

$$ S_1=\frac{B+b}{2}\cdot h \qquad \text{and} \qquad S_2= \frac{B\cdot b}{2} + h.$$

After calculating both values with the data available and obtaining the same result, the student chooses to write in the exam after the calculation of the height

Therefore, the area of the trapezoid is …

without detailing the formula he has used.

We ask if the student made a mistake in obtaining the same value by applying both formulas or, if not, the relationship that exists between the lengths of the bases for this equality to occur.

Solution

Solution proposed by Cristóbal Sánchez-Rubio.

It is evident that the second formula is not an area, it remains to find out if for some value of the measures it can give the same result. The triangles ADD’ and CC’B are similar and both of the type \(30^o-60^o-90^o\), therefore it is clear that $$AD’=\frac{h}{\sqrt{3}}, \quad C’B=h \sqrt{3},$$

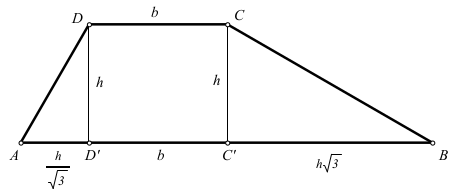
as shown in the figure. In addition

$$B-b= h \Big( \frac{1}{\sqrt{3}} + \sqrt{3} \Big) = \frac{4}{3}h\sqrt{3},$$

therefore

$$h=\frac{\sqrt{3}(B-b)}{4}.$$

If the two formulae yield the same value, it should be

$$ \frac{(B+b)}{2} \frac{\sqrt{3}(B-b)}{4} = \frac{B \cdot b}{2} + \frac{\sqrt{3}(B-b)}{4},$$

clearing \(\sqrt{3}\) results in

$$ \sqrt{3}=\frac{4Bb}{(B-b)(B+b-2)}.$$

This is impossible since, as the bases are integers, the right-hand member is rational and \(\sqrt{3}\) is irrational. Therefore, the student mentioned in the statement was wrong to obtain the same value by applying both formulae.