La comprensión de la turbulencia es uno de los problemas científicos más antiguos y complejos, quizás sólo comparable a la comprensión del funcionamiento del cerebro. Desde las primeras obras de Boussinesq y Reynolds a finales del siglo XIX, que formalizaron las características básicas de los flujos turbulentos, el análisis del comportamiento extremadamente complejo de la turbulencia ha atraído el interés de muchos investigadores.
La cuestión de lo que es la “turbulencia” aún está lejos de ser resuelta, aunque muchas de sus características pueden deducirse de observaciones y experimentos. Los flujos turbulentos tienen un enorme impacto en el desarrollo de la vida humana, desde la predicción del tiempo hasta el suministro de agua dulce, la generación de energía, procesos biológicos, transporte, contaminación, cambio climático… Por lo tanto, la simulación numérica de la turbulencia es de importancia primordial para mejorar la vida humana en muchos ámbitos.

La mecánica de fluidos clásica establece que el movimiento de un flujo viscoso se rige por las ecuaciones de Navier-Stokes, que en teoría deberían ser apropiadas para realizar simulaciones numéricas de flujos turbulentos. Sin embargo, un flujo turbulento es un sistema altamente irregular, caracterizado por cambios quasi-caóticos de su comportamiento que implican una amplia gama de escalas de espacio y tiempo, en interacción no lineal entre sí. Estas características generan una alta complejidad computacional, lo que hace imposible las simulaciones numéricas directas de los flujos turbulentos de las ecuaciones de Navier Stokes.
Se estima que un cálculo preciso de todas las escalas de un flujo turbulento sólo será posible a finales del siglo XXI, si la mejora de los recursos computacionales continúa a la misma tasa.
Para comprender la dificultad de la simulación numérica de un flujo turbulento plenamente desarrollado, hay que empezar por entender qué es el número de Reynolds: El parámetro esencial que determina el comportamiento de un flujo turbulento es el número de Reynolds, que representa la razón entre las fuerzas de inercia y las de viscosidad dentro del flujo. A mayor número de Reynolds, las fuerzas de inercia son mayores, por lo que se generan más torbellinos y el flujo es más y más complejo. Torbellinos grandes tienden a formar otros cada vez más pequeños, lo que consume energía cinética, que es “exportada” de los torbellinos grandes a los pequeños.
El tamaño de los torbellinos más pequeños corresponde a la energía cinética, que es disipada en calor por efectos de rozamiento viscoso entre moléculas, por lo que no puede haber torbellinos de menor tamaño (Figura 1). Al mismo tiempo, los torbellinos evolucionan en “escalas de tiempo” (el tiempo que tardan en experimentar cambios apreciables) igualmente dependientes del juego de fuerzas de inercia-fuerzas de viscosidad.
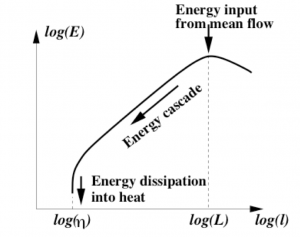
La modelización de la turbulencia está basada en propiedades llamadas “de similaridad” de los torbellinos en un flujo turbulento plenamente desarrollado: En grueso, las propiedades estadísticas de las fluctuaciones turbulentas son las mismas independientemente del tamaño de los torbellinos. La teoría de similaridad fue desarrollada con detalle por Kolmogorov, en 1941, y es la base de la moderna modelización de la turbulencia. En particular, esta teoría proporciona una estimación del tamaño (\(\eta\)) de los menores torbellinos creados en un flujo turbulento en términos del tamaño de los mayores torbellinos (\(L\)) y del número de Reynolds (\(\mathrm{Re}\)):
\(\eta = L\,\,\mathrm{Re}^{-3/4}\)
Por ello, el cálculo preciso del flujo en 3D requerirá un número de nodos del orden de \(\mathrm{Re}^{9/4}\). Este número resulta ser enorme para flujos reales, con números de Reynolds entre \(10^4\) y \(10^{12}\), o incluso mayores. Incluso para el menor de ellos, son necesarios \(10^9\) nodos computacionales.
Una estimación del esfuerzo computacional debe también tener en cuenta el paso de tiempo: Éste debe ser aproximadamente igual a la escala de tiempo de los menores torbellinos. El resultado, discutido en Pope (2000), es que incluso para flujos “simples” (flujo incompresible sin capas límites), el producto del número de nodos computacionales por el número de pasos de tiempo requeridos para simular una evolución típica de un flujo turbulento es aproximadamente \(160 \, \mathrm{Re}^3\).
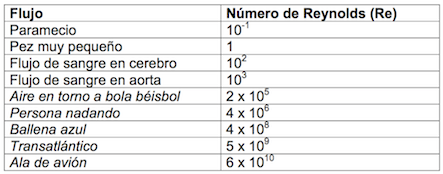
El número de operaciones de coma flotante por nodo computacional y por paso de tiempo varía, dependiendo de la efectividad del método numérico que se use, pero sin duda es mayor que 100. Tomando esta cota inferior, obtenemos una estimación final del número total de operaciones de coma flotante necesitadas para una simulación significativa de un flujo turbulento: en ningún caso será menor que \(10^4 \mathrm{Re}^3\). Considerando un flujo a número de Reynolds moderado, \(\mathrm{Re}=10^6\) (excedido por muchos flujos comunes, ver Tabla 1), el número total de operaciones es cercano a \(10^{22}\). Suponiendo que trabajamos en un servidor multiprocesador con 100 Gflops (\(10^{11}\) operaciones de coma flotante por segundo), los cálculos tomarían \(10^{11}\) segundos. O sea, unos 3000 años… Si ponemos ahora en marcha nuestro servidor, muy posiblemente nadie se acordará de nosotros cuando se acabe el cálculo…
Este ejemplo aclara la dificultad que requiere la simulación precisa de un flujo turbulento. Para remediar esta dificultad se introducen modelos de turbulencia, con el fin de reducir esta complejidad computacional.
Junto a la experimentación y la física, el modelado y el análisis matemático desempeñan un papel central en el estudio de los flujos turbulentos. Las matemáticas proporcionan un apoyo permanente para construir modelos de turbulencia en meteorología, oceanografía, climatología, medio ambiente y aplicaciones industriales. Un ejemplo de particular interés es la predicción del tiempo atmosférico, en la que aproximadamente cada década se avanza en la predicción fiable del tiempo por un día más. A este ritmo, también nos tomará unos 3000 años averiguar qué tiempo hará el año que viene…
Referencias:
- T. Chacón, R. Lewandowski (2014): Mathematical and Numerical Foundations of Turbulence Models and Applications. Birkhauser (2014)
- S. B. Pope (2000): Turbulent Flows. Cambridge University Press (2000).
- A. N. Kolmogorov (1941). Dissipation of Energy in Locally Isotropic Turbulence. Proceedings of the USSR Academy of Sciences (en ruso). 32: 16–18.
- O. Zhikanov (2015): Essential Computational Fluid Dynamics. Wiley (2015).
- O. Zhikanov (2011): Essentials of fluid dynamics, slides, https://umich.app.box.com/s/81xa9ivi5i6f1e3p7ddfxviuw0mjv8jh (2011)

Hola, Tomás
Has hablado de la importancia de las ecuaciones de Navier-Stokes, y que teóricamente deberían ser apropiadas para hacer simulaciones numéricas de flujos turbulentos. Pero me gustaría que nos explicaras que ocurriría si alguien descubriera las soluciones exactas (aparte de ganar un millón de dólares si demostrara además la existencia y regularidad de las mismas). ¿Podrías imaginar cómo sería la física moderna entonces? Se que es muy generalista la pregunta, si quieres puedo concretar más.
Gracias por el artículo y por vuestro blog