Publicamos la solución al divertimento El trozo del cuadrado. Gracias a Floro Damián Aranda Ballesteros, Pablo Cano Wall, Juan Miguel Expósito, Marcos Jiménez y Manuel Zambrana y Cristóbal Sánchez-Rubio por las soluciones que nos han hecho llegar.
Divertimento:
Se une un punto \(P\) en el interior de un cuadrado con los puntos medios de los lados, delimitando cuatro regiones de áreas distintas. Las áreas de tres de estas regiones son números enteros positivos consecutivos. Se pide demostrar que el área de la cuarta región también es un número entero consecutivo con los otros.
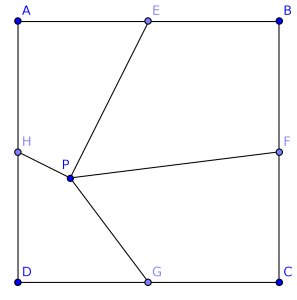
Solución:
Consideremos los segmentos que unen el punto \(P\) con cada uno de los vértices.
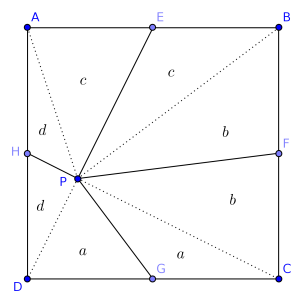
El triángulo \(DPG\) tiene el mismo área que el triángulo \(GPC\), pues tienen igual base y altura. La misma construcción puede hacerse en el resto del cuadrado, de modo que
\begin{equation*}\begin{split}
& \mathrm{área}(DHPG) + \mathrm{área}(PEBF) = (a+d) + (c+b) \\
& \mathrm{área}(AHPE) + \mathrm{área}(GPFC) = (d+c) + (a+b).
\end{split}\end{equation*}
Se deduce que cada región y su opuesta suman el mismo área que las otras dos, es decir,
$$
\mathrm{área}(DHPG) + \mathrm{área}(PEBF) = \mathrm{área}(AHPE) + \mathrm{área}(GPFC).
$$
Denotemos por \(x\), \(x+1\) y \(x+2\) a las tres áreas que sabemos que son consecutivas, y \(z\) al cuarto área. Existen tres posibilidades:
- Si \(x\) es el área opuesta a \(z\), entonces \(x+z = (x+1) + (x+2)\), de donde \(z=x+3\).
- Si \(x+1\) es el área opuesta a \(z\), entonces \((x+1)+z = (x+1) + x\), de donde \(z=x+1\). Este caso no es posible pues las cuatro áreas son distintas.
- Si \(x+2\) es el área opuesta a \(z\), entonces \((x+2)+z = (x+1) + x\), de donde \(z=x-1\).
En ambos casos, \(z=x-1\) o \(z=x+2\), se cumple que las cuatro regiones tienen áreas consecutivas.
Además, Floro Damián Aranda ha determinado las condiciones bajo las que existe un cuadrado como el que se propone: si las áreas son \(n\), \(n+1\), \(n+2\) y \(n+3\), entonces el lado del cuadrado es \(l=\sqrt{4n+6}\) y las coordenadas del punto en el interior son \(P=\left( \frac{2n-1}{\sqrt{4n+6}},\frac{2n+1}{\sqrt{4n+6}} \right)\) (rotando el cuadrado para que la región de área menor tenga su vértice en el origen de coordenadas).

Salvo error, si el eje de coordenadas se sitúa en el centro del cuadrado y considerando que las coordenadas del punto P sean (x,y), la menor de ellas (en valor absoluto) sería igual a 1 entre la mitad del lado, en tanto que la otra sería el doble (en valor absoluto).
Entiendo que hay un pequeño error cuando comenta que Floro Damián dice que el lado sería un entero positivo. A mi entender el lado del cuadrado nunca puede ser un entero atendiendo al siguiente razonamiento.
Sea m el menor entero entre las áreas. Sea a el lado del cuadrado. Entonces tenemos que
a^2 = m+m+1+m+2+m+3 = 4m+6
Por tanto, tomando módulo 4:
a^2 = 2 mod 4
Pero
0^2 = 0, 1^2 =1, 2^2 = 0, 3^2 = 1 mod 4
Es decir, un número entero al cuadrado no puede ser congruente con 2 módulo 4
Hola, Rafael:
Lo de que la raíz de 4n+6 es entera ha sido una errata nuestra al transcribir la solución, ya está corregido. Muchas gracias por avisarnos.
Un saludo,
Alberto
Nada, gracias a vosotros. Solo quería resaltar que, no solo es que puede haber casos en los que el lado del cuadrado sea un número no entero, es que de hecho nunca será un número entero.