Solución: El jardín

Publicamos la solución al divertimento del jardín. Gracias a F. Damián Aranda y Marcos Jiménez y Manuel Zambrana por las soluciones que nos han enviado.

Divertimento:

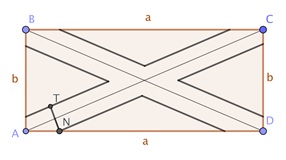
Las dimensiones de un jardín rectangular son números enteros. Se construyen accesos de igual anchura, \(14,\!4\) m (por ejemplo, el segmento \(NT\) en la imagen), que tienen las diagonales como líneas centrales y que resultan ocupar el \(36\%\) del área total del jardín (incluyendo los propios pasillos). Determinar las dimensiones del mismo.

Solución:

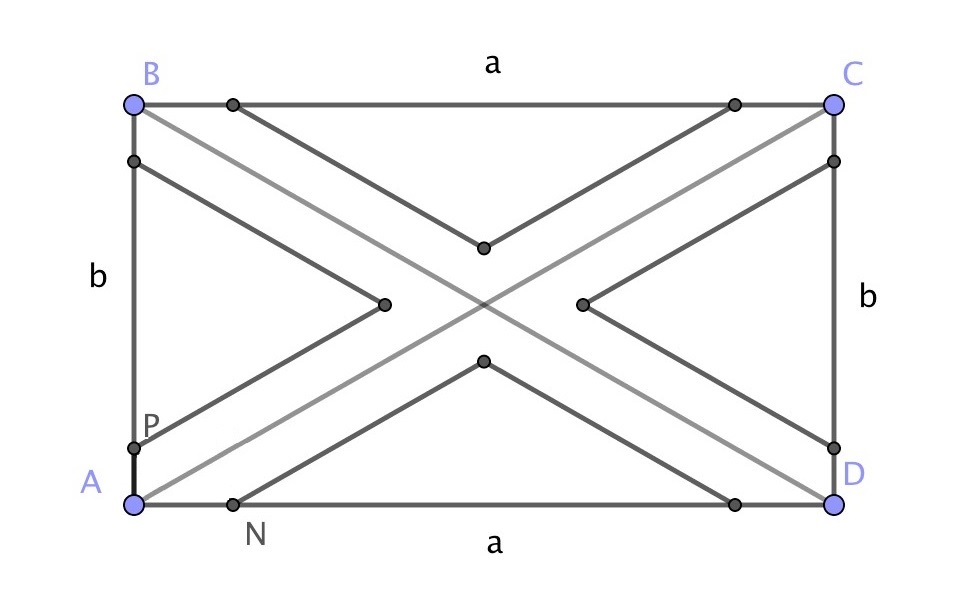
Llamemos \(a>b\) a los lados del jardín. Como los triángulos \(PAN\) y \(BAD\) son semejantes, tenemos que \(AP=AN\frac{b}{a}\).

De esta forma, resulta que la parte exterior a los accesos está formada por dos triángulos isósceles iguales de base \(a-2AN\) y ángulo en la base igual a \(\widehat{CAD}\) y dos triángulos isósceles de base \(b-2AP\) y ángulo en la base complementario a \(\widehat{CAD}\). Estos cuatro triángulos tienen la misma área, que es
$$S=\frac{b(a-2AN)^2}{4a}.$$

De esta forma, la condición del problema es \(4S=0,\!64 ab\), es decir,
$$\frac{b(a-2AN)^2}{a}=0,\!64 ab,$$

de donde se deduce que \(0,\!36a^2-4aAN+4AN^2=0\). De esta ecuación de segundo grado obtenemos que \(a/AN=10\) o \(a/AN=10/9\). Como \(2AN<a\), necesariamente tenemos que

$$0,\!1a=AN=\frac{NT/2}{\operatorname{sen}(\widehat{CAD})}=7,\!2\frac{\sqrt{a^2+b^2}}{b}.$$

En conclusión, \(ab=72\sqrt{a^2+b^2}\). Como \(a\) y \(b\) son enteros, también debe serlo \(\sqrt{a^2+b^2}\), y por tanto los lados del jardín deben formar una terna pitagórica. La forma general de tales ternas es
$$\left\{\begin{array}{l} a=2pqt,\\b=(p^2-q^2)t,\\ \sqrt{a^2+b^2}=(p^2+q^2)t,\end{array}\right.$$

donde \(p>q\) son enteros primos entre sí y \(t\) es un entero arbitrario. Las condiciones que deben cumplir estos números son \(pq(p^2-q^2)t=36(p^2+q^2)\). Como \(p\) y \(q\) no tienen factores primos comunes, \(pq(p^2-q^2)\) debe ser divisor de \(36\) y esto solo se consigue para \(p=2, q=1\). Para estos valores, se obtiene que \(t=30\). De este modo resulta que \(a=120 \text{m}\) y \(b=90 \text{m}\).