Un humorista ilustrado podría hacer un chiste malo contestando que si eres de letras puedes emular a Cervantes y ponerte a escribir una novela, pero si te van más las ciencias puedes darle a la cuadratura del círculo como hizo Anaxágoras en los tiempos de Pericles.
Porque, efectivamente, el origen del problema de la cuadratura del círculo se remonta a los últimos años de Pericles (495-429 a.C.). Después de la etapa gloriosa del apogeo de Atenas, llegó la guerra con Esparta y Pericles se atrincheró dentro de sus murallas. La estrategia podría haber sido buena, pero estalló una epidemia de peste y la ciudad no aguantó. Pericles fue depuesto y murió poco después a consecuencia de la epidemia. «Los ciudadanos de Atenas –escribió Bertrand Russell–, como los de otras ciudades en otras épocas y continentes, mostraron cierta hostilidad a los que intentaron introducir un nivel más elevado de cultura que al que estaban acostumbrados. Cuando Pericles envejeció, sus contrarios empezaron una campaña contra él, atacando a sus amigos. Acusaron a Fidias de haber malversado el oro con el que debía adornar sus estatuas. Dieron una ley permitiendo la denuncia de los que no practicaban la religión. Bajo esta ley persiguieron a Anaxágoras, que fue acusado de enseñar que el Sol era una piedra al rojo vivo». Quizá sea esta de Anaxágoras una de las primeras ocasiones –quizá la primera de la que hay constancia en el mundo occidental– en que lo religioso, constituido en poder fáctico, pretendió reprimir a lo científico. El caso es que el filósofo Anaxágoras acabó en la cárcel acusado de impío. A él se debe el descubrimiento de que la Luna no tiene luz propia sino que refleja la que recibe del Sol, de lo que acabó deduciendo una explicación racional para los eclipses: la Tierra o la Luna ocultan el Sol. Posiblemente los que lo enviaron a prisión nunca supieron a qué dedicó Anaxágoras una parte del tiempo que allí estuvo hasta que Pericles lo liberó –Anaxágoras volvió a Jonia, donde había nacido, y sobrevivió a Pericles en un año–; porque en la cárcel el filósofo se dedicó a cuadrar el círculo.
En la misma formulación de este problema late con fuerza la nueva personalidad que allá por el siglo VI a.C. la revolución pitagórica había impreso en las matemáticas: no se trataba de medir aproximadamente el área de un círculo, tal y como se habían planteado por razones prácticas egipcios o babilonios, sino de medirla en términos exactos, para lo cual había que transformar el círculo –un recinto que no está delimitado por segmentos rectos– en un cuadrado, o en otra figura limitada por lados rectos. La gracia estaba en hacer esa transformación usando exclusivamente regla y compás -para otro tipo de cuadraturas del círculo, véanse las entradas Cuadrando el círculo y La cuadratura del círculo-.
Antes de que los griegos se dieran cuenta de lo endiabladamente complicada –en realidad imposible– que es la cuadratura del círculo, un contemporáneo de Anaxágoras consiguió algunos resultados esperanzadores. Este personaje, tan oculto como Anaxágoras entre las brumas donde la leyenda se confunde con la Historia, se llamó Hipócrates de Quíos –y no hay que confundirlo con el más célebre Hipócrates de Cos, reputado como padre de la medicina y autor del famoso Juramento hipocrático que realizan los médicos–. Hipócrates mostró que al calcular la razón entre el área de un círculo y la del cuadrado levantado sobre su radio, el resultado será siempre el mismo, sea cual sea el tamaño del círculo, aunque no se ha conservado cómo hizo este descubrimiento. A ese «número» que se obtiene al dividir el área de un círculo cualquiera entre su radio al cuadrado es al que hoy llamamos \(\pi\). El que la razón entre el área de cualquier círculo y el cuadrado levantado sobre su radio fuera siempre la misma, con independencia del tamaño del círculo, no resolvía, tal y como lo entendían los griegos, el problema de la cuadratura del círculo, porque esa razón –nuestro número \(\pi\)– mostró ser una cantidad muy poco razonable, tanto que a los griegos \(\pi\) siempre les pareció sospechoso y nunca consideraron que fuera un número, porque nunca lograron mostrar que fuera una fracción –no lo es, de hecho–.
Hipócrates logró también cuadrar varias figuras curvilíneas cercanas al círculo, lo que dio esperanzas de que este también pudiera ser cuadrado. Esas figuras fueron las primeras de la historia en ser cuadradas aun siendo sus lados curvos; son todas de la misma familia y, por razones obvias que ahora se verán, se las llamó «lúnulas». He aquí el ejemplo más sencillo:
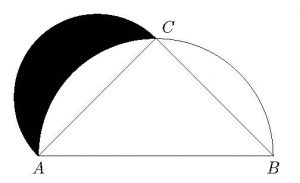
Partimos de un semicírculo con diámetro AB; en el semicírculo se ha inscrito el triángulo isósceles ABC –que tiene dos lados iguales: AC=AB–. Con centro en el punto medio del lado AC se ha trazado una media circunferencia que une los puntos A y C, y define la lúnula sombreada en negro. Hipócrates probó entonces que el área de la lúnula es exactamente igual a la mitad del área del triángulo ABC –la demostración es un bonito reto que el lector de esta entrada no debe privarse de intentar–.
Hay que insistir en que lo que hace al problema de la cuadratura del círculo tan difícil de resolver –en realidad imposible– es respetar la norma de que sólo se puede usar regla y compás. Lo mismo ocurre con otros de los problemas que más fascinaron a los griegos: la duplicación del cubo y la trisección de un ángulo -véase la entrada Problemas matemáticos en tiempos de pandemia: la duplicación del cubo–.
De otra forma, la cuadratura del círculo admite soluciones más o menos ingeniosas y, de hecho, los griegos encontraron algunas. Por ejemplo, la curva llamada cuadratriz: la definió Hipias de Elis en el siglo V a.C. y parece que fue su única contribución a las matemáticas. Hipias fue un sofista algo fatuo a quien Platón criticó en dos Diálogos. La cuadratriz se define por un recurso dinámico. Se considera un cuadrante de círculo inscrito en un cuadrado; se desplaza la base del cuadrado hacia abajo con velocidad constante y, a la vez, el radio del círculo gira en sentido a las agujas del reloj con velocidad angular constante y comenzado en el lado izquierdo del cuadrado, de manera que lado y radio tardan igual tiempo en recorrer cuadrado y cuadrante, respectivamente: la cuadratriz es el lugar geométrico de los puntos de corte del lado con el radio:
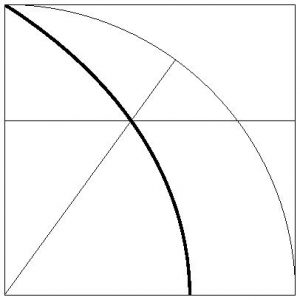
De manera obvia, la cuadratriz permite dividir un ángulo en cualquier proporción dada, y por lo tanto, permite su trisección. Sorprendentemente, también permite cuadrar el círculo usando el segmento que une el centro del círculo con el punto donde la cuadratriz corta a la base del cuadrado -para otras formas geométricas de cuadrar el círculo, véase la entrada Construcción geométrica de Pi-.
Como se comentó antes, el problema de la cuadratura del círculo usando regla y compás es imposible de resolver –al igual que la duplicación del cubo y la trisección de (casi todos los) ángulos–, pero demostrarlo llevó más de dos mil años, y la solución vino del álgebra, no de la geometría. Ahí reside buena parte de la magia de las matemáticas: partes aparentemente desconectadas están unidas de forma tan intensa como profunda, de manera que un problema evidentemente geométrico, como estas particulares construcciones con regla y compás, puede requerir técnicas puramente algebraicas para ser resuelto.
Las construcciones con regla y compás pueden describirse en términos algebraicos: requieren intersecciones de rectas, rectas y circunferencias, o dos circunferencias, lo que equivale algebraicamente a la resolución de sistemas de dos ecuaciones lineales, lineal y cuadrático o, dos ecuaciones cuadráticas. Por tanto, en la descripción de las coordenadas de los puntos del plano que se pueden construir con regla y compas sólo pueden intervenir las operaciones de la aritmética –sumas, productos y divisiones– y las raíces cuadradas. En particular, las coordenadas de estos puntos construibles con regla y compás tienen que ser números algebraicos: esto es, raíces de un polinomio con coeficientes enteros. Así, si pudiéramos construir con regla y compás un cuadrado que tuviera la misma área que un círculo de radio 1, su lado tendría que medir \(\sqrt \pi\), y entonces \(\sqrt \pi\), y por tanto \(\pi\), sería un número algebraico. Ferdinand Lindemann (1852-1939) demostró en 1882 que \(\pi\) es trascendente –esto es, no puede ser raíz de un polinomio con coeficientes enteros–; para lo cual siguió la estela de la demostración de Charles Hermite (1822-1901) de la trascendencia del número \(e\). Lindemann cerró así un reto que costó casi dos milenios y medio superar -sobre resultados de transcendencia véase la entrada Geometría griega, geometría algebraica y transcendencia-.
Referencias
A.J. Durán, Crónicas matemáticas, Crítica, Barcelona, 2018.

Dejar una contestacion