Física y Matemática
Pólya dudaba en el momento de elegir su carrera. Decía que él no era bastante bueno para la Física y era demasiado bueno para la Filosofía. La Matemática está en medio. Yo también me debatía de joven entre estudiar Físicas o Matemáticas, pero elegí las Matemáticas por la Libertad. La Física tiene que explicar el mundo real, en cambio el matemático es libre de crear un mundo y estudiarlo, y, si quiere, puede estudiar el mundo real. Lo cierto es que no es extraño que muchos físicos terminen haciendo matemáticas, demostrando haber hecho una mala elección.
Una estrategia para la prueba de la hipótesis de Riemann es lo que se conoce como la conjetura de Hilbert-Pólya. Se trata de encontrar un operador auto-adjunto en un espacio de Hilbert cuyos autovalores serían las ordenadas de los ceros de la función zeta. Al ser el operador auto-adjunto estos autovalores serían reales. En la Mecánica Cuántica un sistema está gobernado por un operador auto-adjunto: el hamiltoniano. Así que pensaron que un sistema físico adecuado tendría como hamiltoniano el operador del sueño de Hilbert-Pólya. Para mí la Mecánica Cuántica Clásica es una teoría física en pecado. El pecado de no ser relativista y el pecado de no saber bien qué es una observación.
Dicho lo anterior, volvamos a la matemática. Uno debe encontrar un espacio de Hilbert \(H\) y un operador \(D\) en este espacio. Después tiene que probar dos cosas: que \(D\) es auto-adjunto y que los ceros de zeta son todos de la forma \(\frac12+i\lambda\) cuando \(\lambda\) recorre los autovalores de \(D\).
Alain Connes ganó la medalla Fields en 1982 por sus trabajos en Teoría de Operadores. Aparte de un gran matemático es también un físico teórico. Vamos a comentar hoy un trabajo conjunto con Caterina Consani. He de decir que el trabajo es interesante y contiene ideas nuevas y experimentos numéricos que me han sorprendido. No dudo de que las ideas físicas hayan llevado a Connes y Consani a sus sorprendentes resultados. Pero mi objetivo aquí será exponer la parte matemática de su trabajo. Tengo en gran estima a la física, pero creo que en este caso este modo anti-físico aclara mucho lo que realmente tenemos enfrente.

Fórmula explícita de Weil
Debemos empezar por explicar la equivalencia de la hipótesis de Riemann con la positividad de la forma cuadrática de Weil.
Sea \(\mathbb R^*_+\) el grupo multiplicativo de los números reales positivos. La medida de Haar en este grupo es \(\frac{dx}{x}\). Para \(\varphi\in\mathcal C_c^\infty(0,+\infty)\) (funciones indefinidamente diferenciables y de soporte compacto contenido en \((0,+\infty)\)) definimos la transformada de Fourier (o su transformada de Mellin) por $$\widehat\varphi(t)=\int_0^\infty \varphi(x) x^{-it}\frac{dx}{x}.$$
La ecuación funcional de la función zeta nos dice que \(\pi^{-s/2}\Gamma(s/2)\zeta(s)\) toma el mismo valor en \(s\) y \(1-s\), esto implica que es real en la recta crítica y, por tanto, el argumento del factor \(\pi^{-s/2}\Gamma(s/2)\) en la recta $$\vartheta(t)=\mathop{\rm Im}\log\Gamma(\tfrac14+\tfrac{it}{2})-\frac{t}{2}\log\pi,$$ es una función real tal que \(\zeta(\frac12+it)=e^{-i\vartheta(t)}Z(t)\) siendo \(Z(t)\) real. La función \(\vartheta(t)\) es real, muy simple y fácil de calcular. La hemos definido por su papel en la fórmula explícita de Weil. Otro elemento son los ceros \(\alpha\) de la función \(\Xi(t)\), que son tales que \(\frac12+i\alpha\) son todos los ceros complejos de la función \(\zeta(s)\). La hipótesis de Riemann afirma que todos los números \(\alpha\) son reales.
Teorema. (Fórmula explícita de Weil) Para cualquier \(\varphi\in \mathcal C_c^\infty(0,+\infty)\) tenemos $$\sum_{\Xi(\alpha)=0}\widehat\varphi(\alpha) =\widehat\varphi(\tfrac{i}{2})+\widehat\varphi(-\tfrac{i}{2})-\sum_p\sum_{m=1}^\infty \frac{\log p}{p^{m/2}}(\varphi(p^m)+\varphi(p^{-m}))+\frac{1}{\pi}\int_{-\infty}^\infty\vartheta'(t)\widehat\varphi(t)\,dt,$$ donde cada cero \(\alpha\) se repite en la suma de acuerdo con su multiplicidad.
Definimos la forma hermítica de Weil $$W(\varphi_1,\varphi_2)= \sum_{\Xi(\alpha)=0}\widehat\psi(\alpha), \qquad \psi(x)=\int_0^\infty \varphi_1(t)\overline{\varphi_2(t/x)}\frac{dx}{x}.$$ La forma cuadrática de Weil correspondiente se define por \(QW(\varphi)=W(\varphi,\varphi)\).
Proposición. La hipótesis de Riemann es equivalente a la positividad de la forma cuadrática \(QW(\varphi)\ge0\) para cualquier \(\varphi\in\mathcal C_c^\infty(0,+\infty)\).
La forma hermítica (y la correspondiente forma cuadrática) tienen otra expresión dada por el miembro derecho de la fórmula explicita. Vemos que si el soporte de \(\varphi\) está contenido en \([\lambda^{-1},\lambda]\), entonces la suma de los primos en \(W(\varphi,\varphi)\) solo contiene los primos con \(p<\lambda^2\). En particular para \(\lambda=\sqrt{2}\) la suma en los primos es identicamente \(0\).
Yoshida en 1990 comenzó la competición de probar la positividad de \(QW_\lambda\) (la restricción de \(QW\) a las funciones con soporte contenido en \([\lambda^{-1},\lambda]\) para el mayor \(\lambda>1\) posible). Yoshida lo probó para \(\lambda=\sqrt{2}\) cuando los primos no juegan ningún papel. Connes-Consani juegan a esto pero lo que nos interesa es lo que obtuvieron en otra dirección.
Calculando los autovalores de \(QW_\lambda\) directamente
Queremos calcular el menor autovalor de \(QW_\lambda\) para probar que es \(\ge0\). Resulta que son muy pequeños, por ejemplo para \(\lambda^2= 11\) es \(2.389\times10^{-48}\).
Para calcularlos, Connes-Consani convierten el problema en uno discreto.
El sistema trigonométrico usual en \(L^2([-L/2,L/2],dx)\) $$\xi_n(x)=\begin{cases} (-1)^n (2/L)^{1/2} \cos\left(\frac{2\pi n x}{L}\right) & \text{for $n>0$},\\ L^{-1/2}, & \text{for $n=0$,}\\ (-1)^n (2/L)^{1/2} \sin\left(\frac{2\pi n x}{L}\right) & \text{for $n<0$,}\end{cases},\qquad |x|\le L/2,$$ puede transferirse por el cambio de variables \(x\mapsto e^x\) al espacio \(L^2([\lambda^{-1},\lambda],dx/x)\), con \(L/2=\log\lambda\). Por tanto las funciones $$\eta_n(x)=\xi_n(\log x)$$ forman un sistema ortonormal completo en \(L^2([\lambda^{-1},\lambda],dx/x)\).
Connes-Consani toman un número natural \(N\) grande y consideran el espacio \(E_N\) generado por estas funciones \(\eta_n\) con \(|n|\le N\). Calculan la matriz \(W(\eta_n,\eta_m)\) y obtienen el menor autovalor y su correspondiente autofunción como una combinación lineal de las \(\eta_n\) con \(|n|\le N\).
Resulta que la matriz \((W(\eta_n,\eta_m))_{|n|, |m|\le N}\) es simétrica y se anula cuando \(n\ge0\) y \(m<0\). De manera que el operador se descompone en dos correspondientes a las funciones pares e impares $$\varphi(x^{-1})=\varphi(x),\qquad \varphi(x^{-1})=-\varphi(x).$$
Funciones prolate esferoidales
Una de las ideas más interesantes del artículo es reconocer las autofunciones obtenidas por el procedimiento anterior. Pero no se trata de una demostración, es más bien un razonamiento heurístico seguido de una confirmación experimental.
Consideremos un operador \(\mathcal E\) definido en \(\mathcal S_0^{\text{ev}}\), el espacio de la funciones de Schwartz pares y tales que \(f(0)=\widehat f(0)=0\) mediante la fórmula $$\mathcal E f(x)= \sqrt{x}\sum_{n>0}f(nx).$$ Está conectado con la forma cuadrática de Weil por el hecho relativamente fácil de probar que \(QW(\mathcal E f)=0\) para cualquier \(f\in\mathcal S_0^{\text{ev}}\). La demostración es directa usando la definición de \(QW\) mediante los ceros de la función \(\Xi\). Dada una función en el espacio de Schwartz \(f\in\mathcal S_0^{\text{ev}}\) la fórmula de Poisson prueba que $$(\mathcal E\widehat f\;)(x)=(\mathcal E f)(x^{-1}), \qquad x>0, \quad f\in\mathcal S_0^{\text{ev}}.$$
Es natural pensar que los pequeños autovalores de \(QW_\lambda\) correspondan a auto-funciones en las que \(QW(\varphi)=0\). Por esto buscaremos \(\varphi=\mathcal E f\). Como en el caso de las autofunciones de \((W(\eta_n,\eta_m))\), nuestras funciones \(\varphi\) han de ser pares o impares: \(\varphi(x)=\pm\varphi(x^{-1})\). Estas condiciones y la fórmula de Poisson nos llevan a buscar una función \(f\in\mathcal S_0^{\text{ev}}\) tal que \(f(0)=\widehat f(0)=0\), con soporte en \([-\lambda,\lambda]\), tal que \(\widehat f(x)\approx\pm f(x^{-1})\) para \(|x|<\lambda\) y tal que \(\widehat f(x)\) sea muy pequeño para \(x>\lambda\).
Todo esto lleva a pensar en las funciones prolate esferoidales. Estas funciones aparecieron por primera vez en el Análisis como soluciones de una ecuación diferencial de segundo orden que aparece al transformar un operador diferencial a coordenadas prolate esferoidales. Pero deben su importancia a los trabajos de Slepian y colaboradores en los laboratorios de la compañía de teléfonos Bell, que en los años 60 descubrieron su papel en relación a la transformada de Fourier truncada.
El operador de Fourier truncado \(\mathcal F_\lambda\colon L^2[-\lambda,\lambda]\to L^2[-\lambda,\lambda]\) definido por $$(\mathcal F_\lambda\varphi)(x)=\int_{-\lambda}^\lambda\varphi(t)e^{ixt}\,dt$$ es compacto. Existe una sucesión de funciones (las prolate esferoidales) que satisfacen $$\int_{-\lambda}^{\lambda}\psi_{m,\lambda}(x) e^{2\pi i x y}\,dx=\chi_m\psi_{m,\lambda}(y).$$ La sucesión de autovalores \(\chi_m\) tiende a cero, pero para cada valor de \(\lambda\) empieza con varios autovalores muy aproximadamente iguales a \(\chi_m\approx(-1)^m\). Cuando \(\lambda^2\) es un semientero el número de estos autovalores es \(\nu(\lambda^2)\approx 2\lambda^2-1\). Esto corresponde a funciones de soporte compacto cuya transformada es aproximadamente también soportada en el mismo compacto.
Las funciones prolate esferoidales no satisfacen \(f(0)=\widehat f(0)=0\), pero conseguimos otras con la misma paridad y que satisfacen esta condición poniendo $$\begin{aligned} \phi_{2n}(x)&=\psi_{2n}(x)\psi_0(0)-\psi_0(x)\psi_{2n}(0)\\ \phi_{2n+1}(x)&=\psi_{2n+1}(x)\psi_1(0)-\psi_1(x)\psi_{2n+1}(0). \end{aligned}$$ Es fácil calcular los desarrollos de Fourier de las funciones \(\mathcal E \phi_n\) $$(\mathcal E \phi_{n})(x)=\sum_{n\in\Z} a_{n,j}\eta_j(x),$$ truncamos sus desarrollos $$\begin{aligned} (\mathcal E \phi_{2n})(x)\approx\mathcal E_{2n}(x)&:=\sum_{j=0}^N a_{2n,j}\eta_j(x),\\ (\mathcal E \phi_{2n+1})(x)\approx\mathcal E_{2n+1}(x)&:=\sum_{j=1}^N a_{2n+1,-j}\eta_{-j}(x).\end{aligned}$$ Y finalmente ortonormalizamos estas funciones siguiendo el proceso de Gram-Schmidt separadamente en las funciones pares e impares. De este modo obtenemos las funciones \(\varepsilon_n(x)\) para \(2\le n\le \nu(\lambda^2)-1\). Es sorprendente que estas funciones \(\varepsilon_n\) son las autofunciones de la forma \(QW_\lambda\) correspondientes a autovalores pequeños. En el gráfico están representadas las dos autofunciones para \(\lambda^2\) entre \(3.5\) y \(11\), en muchos casos la coincidencia es tal que no se ve más que una.
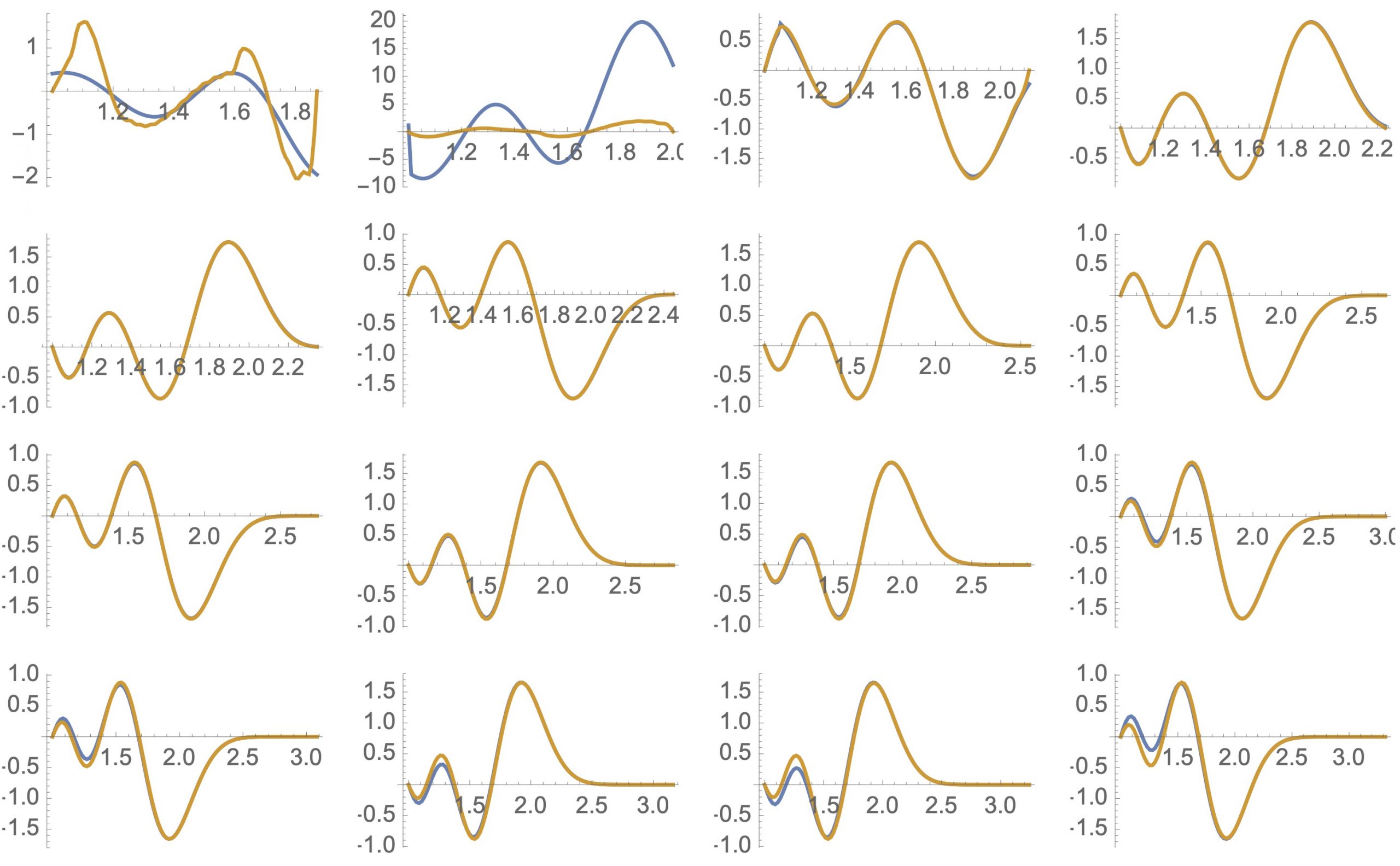
Más sorpresas
Las funciones \(\varepsilon_n\) son ortonormales por construcción. Las primeras \(k\) funciones \(\{\varepsilon_2,\dots,\varepsilon_{k+1}\}\) generan un subespacio \(H_k\) de dimensión \(k\) en \(L^2[\lambda^{-1},\lambda]\), en el espacio ortogonal a \(H_k\) consideramos el operador \(D=-ix\frac{d}{dx}\). Es decir, consideramos el operador $$D(\lambda,k)=(1-\Pi(\lambda,k))\circ D\circ (1-\Pi(\lambda,k)),$$ donde \(\Pi(\lambda,k)\) es la proyección sobre el subespacio \(H_k\) generado antes. Cuando \(k\) es menor pero prácticamente igual a su valor máximo \(\nu(\lambda^2)-2\), se prueba que el número de autovalores de \(D(\lambda,k)\) en el intervalo \((0,E]\) con \(E=2\pi \lambda^2\) es aproximadamente $$\frac{E}{2\pi}\log\frac{E}{2\pi}-\frac{E}{2\pi},$$ tantos como los de la función zeta. Y si vamos a los ejemplos estos autovalores casi coinciden con los de la función zeta.
Lo sorprendente aquí es que la proyección \(\Pi(\lambda,k)\) no ha tenido que ver nada con la función zeta o con sus ceros. Hemos partido de las funciones prolate esferoidales y con ellas hemos construido un espacio, y el operador \(D\) no puede ser más simple. Sin embargo, la coincidencia con los ceros de la función zeta es muy notable. Por cierto, este operador \(D\) fue pronosticado por Connes-Consani en otro artículo anterior basándose en argumentos físicos.
Hay alguna sorpresa más. Connes y Consani representan las funciones \(\lambda_j(D(\lambda,k))\) del \(j\)-ésimo autovalor en función de \(\lambda\):
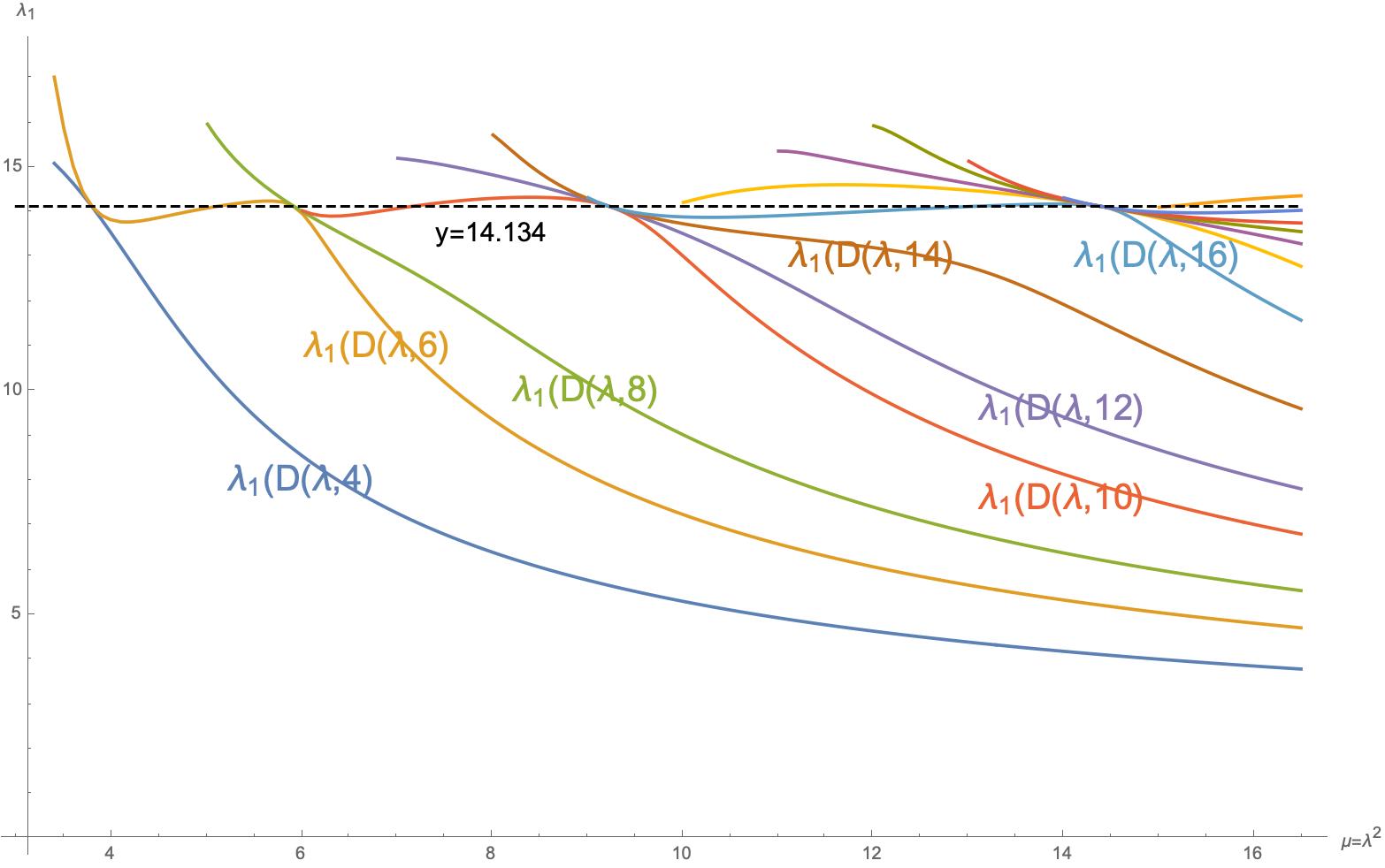
Vemos que estas curvas coinciden en algunos puntos, precisamente cuando toman el valor de la ordenada del primer cero de zeta (o del \(j\)-ésimo) representamos \(\lambda_j(D(\lambda,k))\). Los valores de \(\mu=\lambda^2\) donde se dan estas coincidencias son también notables, precisamente cuando \(\lambda=e^{\pi n/\gamma_1}\) con \(n\) un número natural.
Explicaciones
El trabajo de Connes-Consani contiene un solo teorema importante. Pero es un teorema que da una caracterización de los números reales \(\gamma\), tales que \(\zeta(\frac12+i\gamma)=0\). Lo notable, desde mi punto de vista, es que proporciona una diferencia entre los ceros en la recta crítica y los posibles ceros en la banda pero fuera de la recta, esto es, de las quiméricas excepciones a la hipótesis de Riemann.
[Uso aquí la palabra quimérico porque es lo que la mayor parte de los matemáticos dirían, no yo, que no veo tan improbable su existencia.]
Introducimos otros dos operadores $$(\Sigma_\mu g)(x)=\sum_{k\in\mathbb Z}g(\mu^k x)\qquad \vartheta_\lambda f(x)= f(\lambda^{-1}x).$$ Cuando esté definido se tiene \((\Sigma_\mu g)(\mu x)=(\Sigma_\mu g)(x)\). Así que podemos entender que esta función está definida en \(C_\mu:=\mathbb R^*_+/\mu^\mathbb Z\); este espacio tiene la topología de una circunferencia y puede ser dotado de la medida \(dx/x\).
El principal teorema del artículo es la siguiente caracterización de los ceros de zeta en la recta crítica.
Teorema. El subespacio \(\Sigma_\mu\mathcal E (\mathcal S_0^{\text{ev}})\subset L^2(C_\mu)\) no es denso si y solo si \(\mu=\exp(\frac{2\pi n}{\lambda_r})\) para \(n\in\mathbb Z\) y \(\lambda_r\) cualquier número real tal que \(\zeta(\frac12+i\lambda_r)=0\).
En la situación del teorema tenemos \(x^{i\gamma_r}\in\bigl(\Sigma_\mu\mathcal E (\mathcal S_0^{\text{ev}})\bigr)^\perp\). Y nuestro operador \(D\) cumple entonces $$D(x^{i\gamma_r})=-ix\frac{d}{dx}(x^{i\gamma_r})=\gamma_r x^{i\gamma_r}.$$
En el espacio \(\bigl(\Sigma_\mu\mathcal E (\mathcal S_0^{\text{ev}})\bigr)^\perp\) el operador \(D\) tiene como autofunción a \(x^{i\gamma_r}\) con autovalor justamente \(\gamma_r\).
Vemos pues un camino abierto. En lugar de buscar un operador extraño podemos usar \(D\) (o cualquiera de entre muchos otros que tienen todos los números reales como autovalores) y más bien modificar el espacio de manera que no le queden más que los autovalores \(\lambda_r\). Pero debemos ver qué subespacio escogemos de manera que no dependa de los ceros de zeta. El procedimiento de Connes-Consani no es perfecto porque \(\mu\) está definido a partir de \(\lambda_r\). Pero su trabajo nos da una idea de que debemos mirar al espacio \(E^\perp\), siendo \(E\) el conjunto de funciones que anulan la forma cuadrática de Weil \(QW(\varphi)=0\).
Para saber más
Hay mucho material sobre Alain Connes en internet. Ha publicado libros serios de matemáticas pero también tiene libros hablando de las matemáticas, de la física, de sus relaciones.
El artículo que hemos comentado está colgado en arXiv.
A. Connes y C. Consani, Spectral triples and \(\zeta\)-cycles, https://arxiv.org/abs/2106.01715.
Y hay varias conferencias en internet de Connes explicando este trabajo como, por ejemplo, North Atlantic Noncommutative Geometry Seminar.
Hay otro artículo con Henri Moscovici que está relacionado y no hemos comentado. Connes lo explica en esta conferencia: Conference in honor of Michael Douglas 60th birthday.
Hay muchas conferencias interesantes de Connes en youtube. La mayor parte en francés, pero muy recomendables y fáciles de encontrar. Por citar alguna, Connes fue miembro de Bourbaki y hay conferencia en que hablan varios miembros como Serre, Dixmier o Cartier sobre sus experiencias en Bourbaki y que está dirigida por Connes: Bourbaki, les années 1945-75. Otras: Le quantique, les mathematiques et le temps, y Alain Connes – «Espace temps, nombres premiers, deux défis pour la géométrie».
Pregunté a Connes por qué usa justo el operador \(-ix\frac{d}{dx}\), que él denomina operador de Dirac. Me remite a su trabajo: A. Connes, C. Consani, The Scaling Hamiltonian, arXiv:1910.14368, que como vemos es del año 2019.
A mi pregunta de cómo construir el espacio adecuado para la conjetura de Hilbert-Pólya, Connes me dirige al trabajo A. Connes, C. Consani, Hochschild homology, trace map and \(\zeta\)-cycles, arXiv 2207.10419.
Los intentos de relacionar la física con la hipótesis de Riemann son abundantes y no siempre afortunados, una recopilación puede encontrarse en D. Schumayer, D. A. W. Hutchinson,Physics of the Riemann Hypothesis, arXiv:1101.3116.
La frase de Polya esta sacada de
Las funciones prolate esferoidales son especialmente interesantes. Actualmente hay una buena referencia:
A. Osipov, V. Rokhlin, Hong Xiao, Prolate Spheroidal Wave Functions of Order Zero, Springer, 2013.
La imagen destacada es la Grevillea ‘Moonlight’. Los filamentos de sus flores son comparables a los ceros de la función zeta.


Dejar una contestacion