Solar energy (I): positioning, cleaning and directing mirrors

Clean sources of energy are needed to gradually replace traditional sources. The climate deterioration we are suffering urgently demands it.

One source of energy that is inexhaustible in practice is the Sun. In fact, one hour of solar radiation is equivalent to the electricity consumed in one year worldwide. It therefore seems natural and logical that we should seek to promote research and development of solar energy.

The context

Worldwide, the country with the most solar power installations is China; in Europe, it is Germany (followed by Spain). Germany aims to base its entire consumption exclusively on renewable energies by 2050 at the latest.

In Spain, the autonomous region with the largest number of solar installations is Andalusia, which was also the first in Europe to put into operation a solar thermal power plant.

Nowadays, solar energy is trendy. There are even jokes about it and its use. For example:

“Why are solar panels always optimistic?—They always keep their sunny side up.”

“What is a solar panel’s favourite song?—Here comes the Sun”, and so on.

Many celebrities have also set their own examples in favour of using solar energy for every possible purpose: Brad Pitt, Leonardo DiCaprio, Julia Roberts, Johnny Depp, Rachel McAdams, Penelope Cruz, etc.

Moreover, the authorities have been incorporating solar energy into the lighting of more and more monuments: among others, the Eiffel Tower, the Vatican, the White House and the Mosque of Cordoba; the latter has been using exclusively renewable energies since 2005.

Interestingly, the Dutch company Lightyear recently announced the definitive version of the first solar electric car, the Lightyear 0. Among other features, it is capable of lasting seven months without recharging.

Past and present

Lucian of Samosata (125-181) was a Syriac writer who used the Greek language for his work. He is considered a true master of satire and a pioneer of science fiction. He tells in one of his works that Archimedes, using concave mirrors (also called ustorii), burned the ships of the Roman general Marcellus during the siege of Syracuse.

The authenticity of this story has been the subject of debate for many years: Athanasius Kircher (1601-1680), one of the most important scientists of the Baroque era, went to Syracuse and “proved”, with the help of five mirrors, that a temperature high enough to burn ships could be obtained; René Descartes (1596-1650) suggested, however, that only the ignorant could believe such things; Georges Louis Leclerc, Comte de Buffon (1707-1788), French geographer, biologist, mathematician and writer, installed a huge concave mirror in Le Jardin du Roi in Paris and managed to set fire to various objects and even a whole house from a distance; more recently, in 1973, the Greek engineer Ioanis Sakka was able to set fire to a model of a Greek ship; in 1977, the British physicist and mathematician Dennis L. Sims demonstrated in a paper that Archimedes did not have the means to build mirrors to concentrate sufficient solar energy; finally, a group of students at the Massachusetts Institute of Technology (MIT) concluded that it would only have been possible to set fire to Marcellus’ ships if they had been motionless for several minutes.

However, the idea behind Archimedes’ “possible” feat, harnessing solar energy for our benefit, has been successfully practised since ancient times: the Egyptians and the Greeks used sheets of copper or silver to reflect and concentrate sunlight and, among other things, to heat water; the Romans also used glass to concentrate light and increase lighting and heat in dwellings, and so on.

The use of solar energy as an alternative to fossil fuels actually began in 1866, thanks to Auguste Mouchout (1825-1911), who was able to build the first solar engine, with a parabolic reflector and a cylindrical boiler, capable of driving a steam engine. Unfortunately, the booming trade of the time and the improvement of the railway network made coal supplies cheaper and turned solar power uneconomical. Due to the lack of funding for his proposals, Mouchot devoted himself to teaching and eventually died in poverty.

His is the following sentence:

“Eventually, industry will find no more resources in Europe. We will certainly run out of coal, so what will the industry do?”

At present, the best known forms of solar energy are:

• Photovoltaic energy, for production and consumption at household level; increasingly in demand, especially in recent times, given the huge rise in electricity and gas prices.

• Solar thermal energy, for medium to large-scale production; this is the main topic of this entry.

What both energies have in common is the use of the sun’s radiation. Solar thermal energy concentrates sunlight and converts it into heat; photovoltaic technology, on the other hand, converts solar radiation directly into electricity.

Solar thermal energy can be generated in various ways. The tools used to date are:

• Cylindrical-parabolic collectors that follow the sunlight in order to concentrate the rays on their focal line. In recent times, segmented mirrors have been used to reduce costs (at the cost of a certain loss of efficiency).

The first large-scale parabolic trough plant was conceived and built by the American engineer Frank Shuman (1862-1918) in 1913 in Maadi, Egypt. It was capable of driving a 60-70 hp engine that pumped more than 20,000 litres of water per minute from the Nile to the adjacent cotton fields. Unfortunately, the installation was destroyed during the First World War and was never rebuilt afterwards.

Between 1984 and 1991, the SEGS-1 to SEGS-9 plants were built in the Mojave Desert (California), with an installed capacity of 354 MW. Again, these are concentrating solar power systems based on parabolic trough collectors, this time connected to the electricity grid. These plants were the only commercial plants built before 2007, when it was the turn of the Spanish company Abengoa-Solar.

• Central receiver systems (or tower systems), which use a field of “heliostats” that direct the reflected rays towards a receiver on top of a tower and convert the solar energy into heat, then into mechanical energy and finally into electrical energy.

This technology began to be taken seriously in Sanlúcar la Mayor (Seville) in 2007, with the construction of the PS10 and PS20 plants. Today, there are more than 50 such plants, of different sizes and performance, spread all over the world.

Recently, the “old” parabolic trough plants SEGS-1 to SEGS-9 have been shut down, while the world’s largest tower plant (IVANPAH) was built nearby.

• Parabolic dishes that concentrate sunlight between 1000 and 4000 times on their focus, where a Stirling engine is normally installed. These are very promising systems that have proven to be more efficient than the previous ones, although they are currently in the development phase.

About tower technology facilities

The tower system consists of several elements:

1. A set of mirrors (heliostats) spread across the span of an enclosure.

2. A strategically placed tower supporting a radiation receiver.

Simply described, the operation of each of the elements is as follows:

1. Sunlight is reflected by mirrors and redirected towards the receiver.

2. The light produces a considerable amount of thermal energy which is transmitted to a suitable system of tubes attached to the walls of the receiver. These contain a fluid which, as a result of the applied energy, flows at high speed.

3. The fluid flows through the system of tubes and ends up in a turbine which, as it moves, generates electrical power.

The geographical area occupied can be circular, rectangular, etc. Moreover, in the same field there can be one or several towers and one or several receivers per tower.

The first interesting mathematical problem that arises is to find out where to place the mirrors optimally. Naturally, the concept of optimality has to be specified and, furthermore, a number of practical constraints have to be taken into account.

Another important problem, linked to the operation of the field, is to determine the best way in which the heliostats should be cleaned. This can be formulated as an integer programming problem and can be treated as such. Note that for a field of the usual size, with thousands of mirrors, this question is far from straightforward.

Let us also mention that the appropriate performance of a field makes it necessary to determine a good focussing strategy. In practice, this means that the different illumination zones of the receiver must be “allocated” to the different heliostats (or groups of heliostats) in such a way that the desired temperatures are reached and, if possible, no thermal overload occurs in any zone. Depending on the level of complexity of the model we choose, the determination of an optimal strategy can also be formulated as an extremal problem that can be of the integer or non-integer programming kind or even an infinite-dimensional problem.

About storage

A well-known political leader said several months ago the following:

“The left does not like nuclear and they do not like coal and they not like gas and they do not like hydro and they do not like wind now, and they complain that windmills damage the landscape. Of course, they only like solar energy. So do I. But the day before yesterday at eight o’clock in the evening was the peak of electricity consumption. And at eight o’clock in the evening, I do not know if you were around, but there was no chance that solar would emit. Basically, because it was night. So it is a question of logic.”

Perhaps no one had warned him that the solar energy produced by a family installation can be accumulated throughout the day, so that it can be used during the hours when there is no sun. You should have to be well-informed before talking like that, mate …

It is true, however, that storage is fraught with technical difficulties, especially if it is desired in the medium or long term. Energy from the sun is first stored in the form of heat and then converted into electricity. This raises the possibility of storing part of the thermal energy produced and making it available at a later date when needed. This would make it possible to generate electricity with solar technology at night …

Thermal energy can be stored (at least) in three different ways: by increasing the temperature of a medium, by causing a phase change (from solid to liquid or from liquid to vapour) or by initiating reversible chemical reactions. These three directions are currently being pursued intensively.

Around 2017, a system was designed at Chalmers University of Technology, called “MOST”: Molecular Solar Thermal Energy Storage Systems, based on a specially designed molecule of carbon, hydrogen and nitrogen, which changes shape when it comes into contact with sunlight. It is transformed into an isomer that can be stored in liquid form for later use. A suitable catalyst reverses the situation and returns the molecule to its original form, releasing the previously stored energy.

Kasper Moth-Poulsen, professor in the Department of Chemistry and Chemical Engineering at Chalmers, and his team have recently refined the system to the point where it is now possible to store the energy for several years. An “ultra-thin” chip that could be integrated into small electronic devices converts stored solar energy into electricity. Although much remains to be done, these ideas are very promising.

From a mathematical point of view, the storage problem is also of interest. For example, let us assume that the configuration of a field has been determined and that we know what is the maximum “usable” thermal energy, i.e. that can be converted into electrical energy during the day. In a scenario of excess of thermal energy during sunshine hours, is there an optimal consumption-storage mechanism (in the sense of harnessing as much of the energy produced as possible)? If the answer is yes, how can it be determined?

Furthermore, accepting that it is possible to profit from surplus production, is there an optimal consumption-storage-sale mechanism? How can it be determined?

Learn more (I): how to place mirrors.

Let’s consider the extremal problem
$$
\left\{
\begin{array}{l} \displaystyle
\hbox{Maximize } { {e(\mathbf{x})/c(\mathbf{x})} }
\\ \displaystyle
\hbox{Subject to } { \mathbf{x} \in F, \ \Pi(\mathbf{x})\geq \Pi_0 }
\end{array}
\right.
$$

The variables or unknowns are the positions of the heliostats:
$$
{ \mathbf{x}=\left\{ (x_i,y_i) \in \mathbf{R}^2 : i=1,\dots,N \right\}. }
$$

It is important to keep in mind that the dimension \(N\) of the problem is finite, of the order of \(10^3\) or larger, but unknown a priori. The admissible set where we must find the maximum is
$$
{ F := \{ \mathbf{x} : (x_i, y_i) \in D, \ { |(x_i, y_i)-(x_j, y_j)| \geq \delta} \ \mbox{ for } i \neq j \}. }
$$

The target function is \({ \mathbf{x} \mapsto {e(\mathbf{x})/c(\mathbf{x})}}\), where \(e(\mathbf{x})\) is the annual amount of energy produced and \(c(\mathbf{x})\) is the total cost of the facility. It is understood that \(F\) is the family of admissible positions. On the other hand, there is the constraint function \(\mathbf{x} \mapsto \Pi(\mathbf{x})\), where \(\Pi(\mathbf{x})\) is the power that the field reaches in a prefixed time \(T_d\).

The expression for \(c(\mathbf{x})\) is simple. Conversely, \(\mathbf{x} \mapsto e(\mathbf{x})\) is a complicated function. More precisely, the contribution of the \(j\)-th heliostat to the value of \({ e(\mathbf{x})}\) is
$${
e_{j} = \sum_{n=1}^{365} \int_{I^n} q_n(j,t) \,dt \simeq \int { p}(j,t)\, dt, }
$$

where

• The \(t \mapsto { p}(j,t)\) are polynomial interpolation functions,

• \({ q_n(j,t) := \sum_{i=1}^N q_{(i,n)}^*(j,t) }\) is the effective energy generated at the instant \(t\),

• \(q_{(i,n)}^*(j,t) = r_n(t) A_i(t) \prod_{\ell=0}^4 \nu^\ell_{(i,n)}(j,t) + B_i(t)\) for certain functions \(r_n\), \(A_i\) y \(B_i\), where

• \({ \nu^\ell_{(i,n)}}\) is the \(\ell\)-th efficiency factor corresponding to the \(i\)-th heliostat and to the \(n\)-th day of the year.

Efficiency factors are due to atmospheric, radiation, orientation and proximity circumstances and other factors. For example, we have expressions such as the following, which give an idea of the complexity of the target function:
$$
\begin{array}{l} \displaystyle
{ \nu^0}=\alpha_1- \alpha_2 \rho(i,Q_E)+\alpha_3 \rho(i,Q_E)^2, \ \ { \nu^1}=S_Ec_R,  \ \ { \nu^2} = \cos(\gamma(t) /2), \\
\displaystyle
{ \nu^3} = K_{(i,n)}(j,t) \int\!\!\int_S \exp\Big(-\frac{g_1(x,y)}{2\left(\sigma_{(i,n)}(j,t)\right)^2}\Big) \,dx\,dy, \dots
\end{array}
$$

This is a complicated problem (non-convex, of moderate or large size). The existence and uniqueness of the solution, the possible characterisation of the solution(s) and of course the design of convergent algorithms are non-trivial issues.

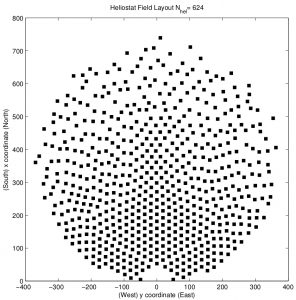
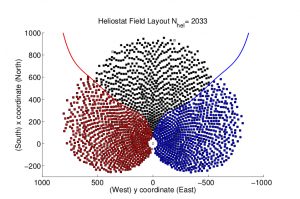
Some real solar thermal fields are the so-called PS10, RPS10 (re-optimised PS10) and SPS10 (spiral version of the PS10 field). In all of them, the arrangement of the heliostats is determined by pre-decided criteria.

Alternatively, we have applied a greedy algorithm to calculate the heliostat distribution in a field of similar size to the previous ones. The algorithm works as follows:

(a) First, we optimally place a single heliostat. To do this, we exhaustively explore the values of the cost function until we reach an acceptable numerical minimum.

(b) Then, taking into account the position of this one, we place a second heliostat also optimally, respecting the constraints of the problem.

(c) We repeat the operation with two heliostats, thus positioning a third one, etc.

(d) We stop the process when the power limit \(\Pi_0\) is reached.

The result was the GPS10 field. As a validation of the quality of the performed calculations, we present in Table 1 values that allow us to compare the performances of GPS10 and the other previous plants.

In particular, we see that GPS10 is admissible as an initial configuration for the determination of a “quasi-optimal” (or optimal) field, e.g. from local refinements.

Learn more (II): some references

For general information on solar thermal energy, see for example:

1. C.J. Winter, R.L. Sizmann, and L.L. Vant-Hull, Solar power plants: fundamentals, technology, systems, economics, Springer-Verlag, 1991.
2. J. Duffie and W. Beckman, Solar Engineering of Thermal Processes, Madison: John Wiley & Sons, Inc., 2006.
3. O. Behar, A. Khellaf, K. Mohammedi, A review of studies on central receiver solar 
thermal power plants. Renew. Sustain. Energy Rev. 2013; 23:12–39.
4. D.R. Mills, Advances in solar thermal electricity technology. Sol Energy 2004; 76:19–31.

For the resolution of heliostat placement, maintenance and orientation problems, see the following works and the references given therein:

1. E. Carrizosa, C. Domínguez-Bravo, E. Fernández-Cara, M. Quero,
   A heuristic method for simultaneous tower and pattern-free field optimization on solar power systems, Computers & Operations Research, Volume 57, 2015, Pages 109-122.
2. T.I. Ashley, E. Carrizosa, E. Fernández-Cara. Heliostat field cleaning scheduling for Solar Power Tower plants: A heuristic approach. Applied Energy 235 (2019) 653–660.
3. — Optimisation of aiming strategies in Solar Power Tower plants. Energy 2017.
4. — An extremal problem with applications to renewable energy production, Math. Model. Nat. Phenom. 16 (2021) 37.

For details on the storage problem, see:

1. M. Khalid, R. Walvekar, H. Panchal, M. Vaka, Solar Energy Harvesting, Conversion and Storage. Materials, Technologies and Applications. Elsevier (to appear in 2023)
.
2. https://news.cision.com/chalmers/r/converting-solar-energy-to-electricity-on-demand,c3540525