We publish here the solution to the divertimento about the geometric construction of pi. The problem is extracted from a paper by Thomas Osler.
Divertimento
Justify the following construction:
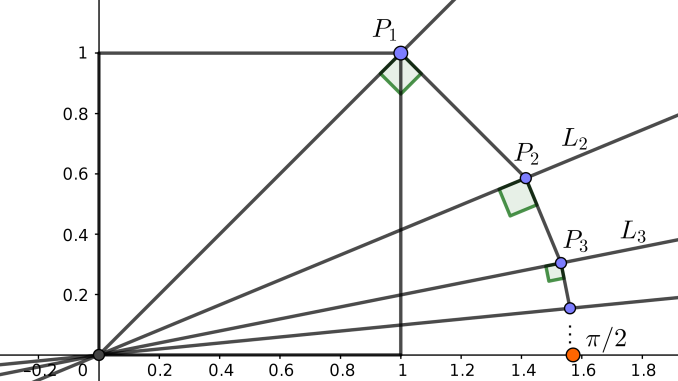
- Draw the unit square and the diagonal \(L_1\) passing through the origin and the vertex \(P_1\) .
- We draw the bisector \(L_2\) of the angle \(L_1\) with the horizontal axis. Draw the perpendicular to \(L_1\) through \(P_1\), which cuts the bisector at point \(P_2\).
- We repeat the process: we draw the bisector \(L_3\) of the angle that \(L_2\) forms with the horizontal axis and we draw the perpendicular through \(P_2\), which cuts \(L_3\) at the point \(P_3\), and so on and so forth.
- The sequence of the lengths of the segments converges to \(\pi/2\).
Hint: We consider the following formula of Viète to be valid:
$$\frac{2}{\pi} = \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{\frac{1}{2} + \frac{1}{2} \sqrt{\frac{1}{2}}}} \cdots$$
Solution
As proposed by Alberto Castaño.
Let \(l_1=\sqrt{2}\) be the distance from the diagonal of the square, \(OP_1\), and let \(P_0\) be the point \((0,1)\). Thus we know that \(c_1:=\cos(\widehat{P_0OP_1})=\cos(\pi/4)=1/\sqrt{2}\).
We now prove by induction that $$(*) \qquad l_n:=OP_n=\left(\prod_{i=1}^nc_i\right)^{-1},$$ where the \(c_i\) are recursively constructed as $$c_k=\sqrt{\frac{1}{2}+\frac{1}{2}c_{k-1}},$$ \(c_1\) being \(1/\sqrt{2}\) as above.
First, we must note that \(c_n=\cos(\pi/2^{n+1})\). Indeed, if \(n=1\) it is true, and for any \(k\), assuming it to be true for \(c_{k-1}\), we have that $$c_k=\sqrt{\frac{1+c_{k-1}}{2}}=\sqrt{\frac{1+\cos(\pi/2^k)}{2}}=\cos(\pi/2^{k+1}),$$ using the formula for the cosine of the half-angle.
Let’s now take any \(r\) and assume formula (*) for \(l_{r-1}\) holds. As the triangle \(OP_{n-1}P_n\) is right, we can express \(l_r=OP_r\) as $$l_{r-1}\cos(\widehat{P_{r-1}OP_r}).$$ Now, \(\widehat{P_{r-1}OP_r}=\pi/2^{r+1}\), therefore $$l_r=\left(\prod_{i=1}^{r-1}c_i\right)^{-1}c_r^{-1}.$$
In conclusion, when we repeat this process indefinitely, we get to $$\lim_{n\rightarrow\infty}l_n=\left(\prod_{i=1}^\infty c_i\right)^{-1}=(2/\pi)^{-1}=\pi/2.$$
As proposed by Cristóbal Sánchez-Rubio.
Calling \(a_k\) to the length of the segment \(OP_k\), we have $$\frac{a_{k-1}}{a_k} = \cos \frac{\pi}{2^{k+1}},$$ and as \(a_1 = \sqrt{2}\), it follows that $$\displaystyle a_k = \frac{\sqrt{2}}{\prod_{n=2}^k \cos \frac{\pi}{2^{n+1}}}.$$ In order to calculate $$\prod_{n=2}^\infty \cos \frac{\pi}{2^{n+1}}$$ we will use the equation discovered by Euler $$\sin x = x \prod_{n=1}^\infty \cos \frac{x}{2^n},$$ which can be found in the book Trigonometric Delights by Eli Maor.
Making \(x=\pi/2\), we get $$1 = \frac{\pi}{2} \prod_{n=1}^\infty \cos \frac{\pi}{2^{n+1}}=\frac{\pi}{2} \cos \frac{\pi}{4} \prod_{n=2}^\infty \cos \frac{\pi}{2^{n+1}},$$ so $$\prod_{n=2}^\infty \cos \frac{\pi}{2^{n+1}} = \frac{4}{\pi \sqrt{2}}.$$ Therefore $$\lim_{n \to \infty} a_n = \frac{\pi \sqrt{2}\sqrt{2}}{4} = \frac{\pi}{2}.$$

Leave a Reply