Publicamos la solución al divertimento de la sombra del triángulo. Muchas gracias a F. Damián Aranda Ballesteros, D. Diedro y D. Pablo, Antonio Medinilla Garófano y David Ramos Orozco y Julio Ojeda Infantes y Pablo Puerto Muñoz por las soluciones que nos han enviado. Los cuatro grupos enviaron unas soluciones de una gran calidad y, lo que es aún más notable, ¡cada una siguió un argumento distinto para probar el resultado!
Divertimento
Supongamos que tenemos un foco de luz que se puede desplazar a lo largo de una recta \(g\) paralela al suelo \(f\) y que hay un cuerpo de forma triangular \(ABC\) suspendido del techo por hilos sin grosor. ¿En qué punto de \(g\) habría que colocar el foco para que la sombra que proyecte el triángulo \(ABC\) sobre \(f\) tenga longitud mínima?
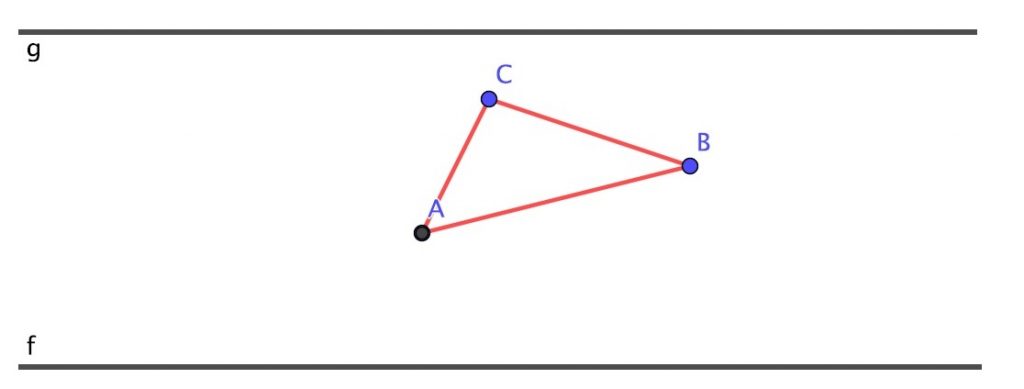
Solución
Como decimos en la introducción, podríamos incluir aquí cualquiera de las soluciones recibidas, pero dejaremos la que teníamos preparada sin desmerecer a ninguna de ellas.
Trazamos paralelas a la línea del suelo por los vértices del triángulo y se pueden dar dos casos: en el primero hay un vértice desde el cual la paralela corta a un lado del triángulo, en el segundo un lado del triángulo es paralelo a la línea del suelo. Veamos el primero:
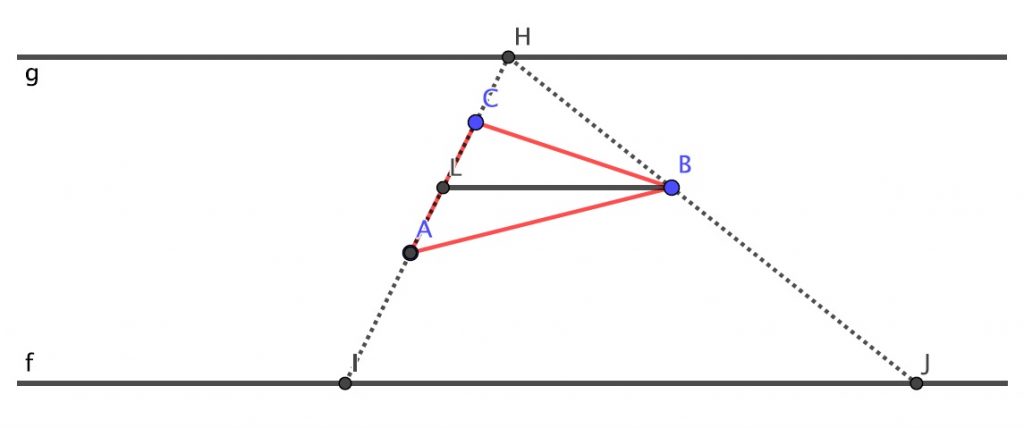
Se prolonga dicho lado hasta la línea del foco y ese es el punto, \(H\), desde el cual la sombra es mínima. Probemos que la sombra desde cualquier otro punto de \(g\) es mayor que \(IJ\). En efecto, sea \(M\) otro punto y sea \(ON\) la sombra proyectada desde ese punto. Se trata de probar que \(IJ<ON\).
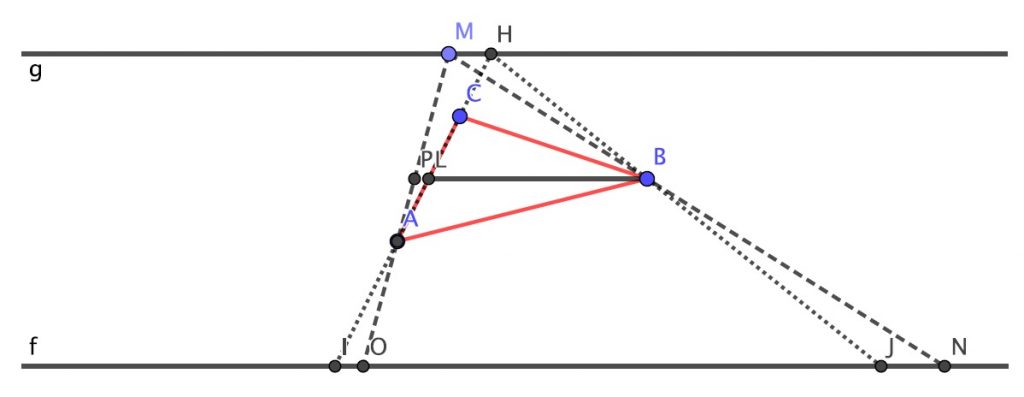
Se prolonga el segmento \(BL\) hasta que corta a \(MO\) en \(P\), que está fuera del triángulo. Los triángulos \(HLB\) y \(HIJ\) son semejantes y la razón de semejanza es \(\frac{LB}{IJ}\). De forma análoga, los triángulos \(MPB\) y \(MON\) son también semejantes y su razón de semejanza es \(\frac{PB}{ON}\). Además ambas parejas de triángulos tienen la misma razón de semejanza, porque \(HLB\) y \(MPB\) tienen la misma altura y también los tienen \(HIJ\) y \(MON\). Por consiguiente,
$$\frac{LB}{IJ}=\frac{PB}{ON}.$$
Y ya que \(LB<PB\), se sigue que \(IJ<ON.\)
Veamos ahora el segundo caso. Prolonguemos los lados \(AC\) y \(BC\) que cortan a \(g\) en los puntos \(V\) y \(T\), respectivamente. Es fácil probar que la sombra desde cualquier punto del segmento \(TV\) es constante y es una sombra menor que la producida cuando el foco está fuera de dicho segmento
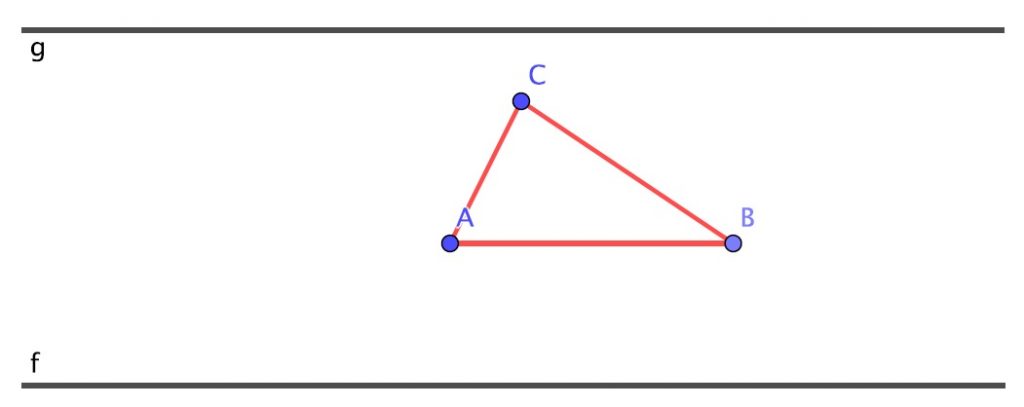
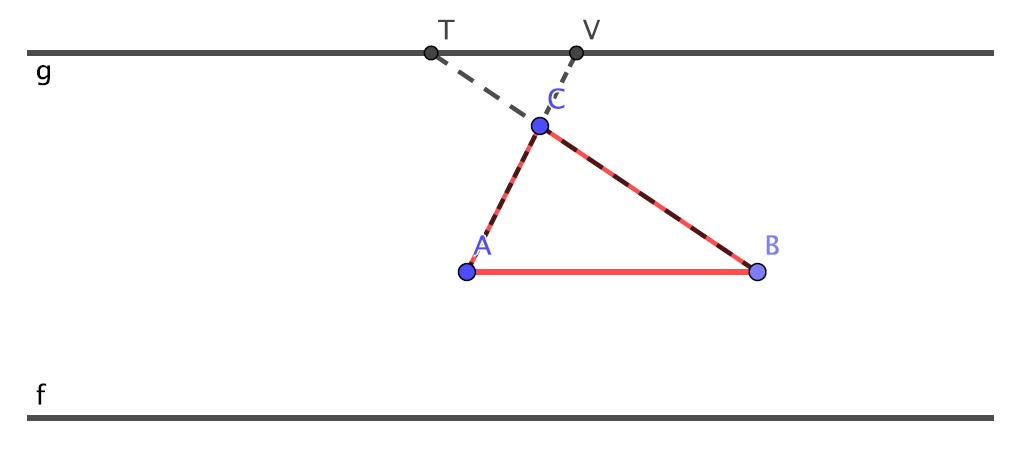
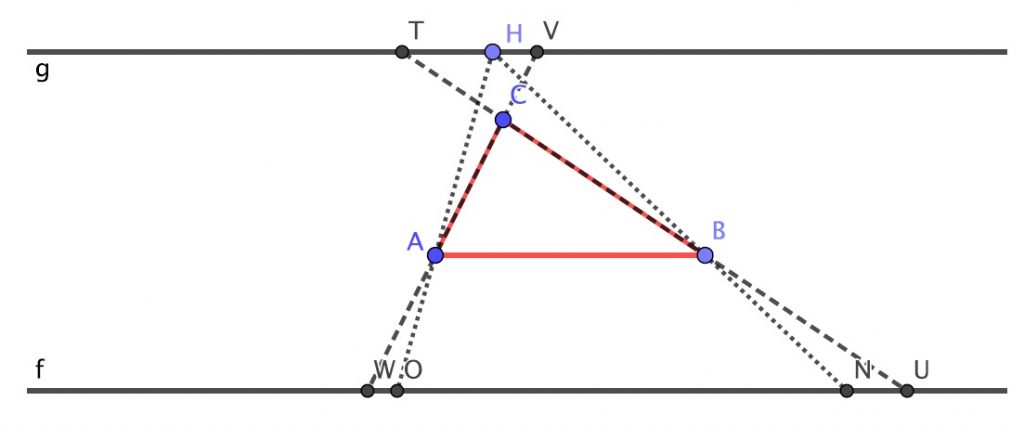
En efecto, si \(H\) es un punto cualquiera de dicho segmento, las rectas que determinan los extremos de la sombra \(HO\) y \(HN\) pasan por \(A\) y \(B\) respectivamente y el mismo argumento de semejanza anterior prueba que la longitud del segmento \(ON\) es constante. Asimismo, si el foco se toma fuera del segmento \(TV\), una de las rectas que determinan los extremos de la sombra pasará por \(C\), y esta recta cortará a la prolongación de \(AB\) en un punto exterior al triángulo. El mismo argumento de semejanza anterior prueba que la sombra tendrá longitud mayor que \(ON\).

Dejar una contestacion