Solución: Un truco de cartas

Publicamos la solución al Divertimento Un truco de cartas. En esta ocasión, Floro Damián Aranda, Juan Miguel Expósito, Antonio Medinilla Garófano y David Ramos Orozco, Don Pablo y Don Diedro y Rubén Ríos Mallqui han enviado respuestas acertadas.

Divertimento:

Un truco de magia con cartas relativamente conocido consiste en dar a un participante una baraja de 27 cartas, de la que debe seleccionar una, y sin mostrárnosla, devolverla a la baraja, que se mezcla. Entonces distribuimos las cartas cara arriba en 3 montones, de izquierda a derecha y una cada vez, para que el participante nos señale cuál es el montón que contiene su carta. Dicho montón se coloca entre los otros dos. Esta rutina se repite otras dos veces más: distribuir las cartas cara arriba de izquierda a derecha en tres montones, señalar el montón con la carta seleccionada, y colocarlo entre los otros. En ese momento, la carta que se busca siempre está en la posición número 14.

Proponemos una variación del juego anterior: damos a un participante una baraja con 27 cartas para que seleccione una, y sin enseñárnosla, la devuelva a la baraja, que se mezcla. Se reparten las cartas en 9 montones cara arriba, una cada vez y siempre de izquierda a derecha. El participante señala el montón que contiene su carta. Ese montón se coloca en tercer lugar comenzando desde arriba (la colocación del resto de montones no afecta). Estamos interesados en determinar cuántas veces hay que repetir esta rutina para asegurar que la carta buscada estará en cierta posición, para lo que se propone:

1. Denotemos por \([1:27]\) al conjunto de los números enteros entre \(1\) y \(27\). Determina la expresión de la función \(H:[1:27] \to [1:27]\) que transforma la posición \(x \in [1:27]\) de la carta escogida por el participante en su posición \(H(x) \in [1:27]\) tras separar en nueve montones y colocar el montón al que pertenece la carta en tercer lugar.
2. Determina los puntos fijos de \(H\).
3. Calcula las potencias de \(H\) necesarias hasta determinar las iteraciones que hay que hacer para determinar la posición de la carta pensada, y cuál es dicha posición.

Solución:

Solución enviada por Rubén Ríos Mallqui.

Vamos a utilizar la función techo \(\lceil x\rceil\) para dar una expresión de \(H\). La posición de la carta \(x\) es \(H(x)=\lceil x/9 \rceil + 6\), pues se colocan \(6\) cartas sobre esta, y \(\lceil x/9 \rceil\) describe la posición relativa en su montón.

Para hallar el punto fijo resolvemos la ecuación \(\lceil x/9 \rceil + 6=x\). Gráficamente, se observa que la única solución es \(x=7\).

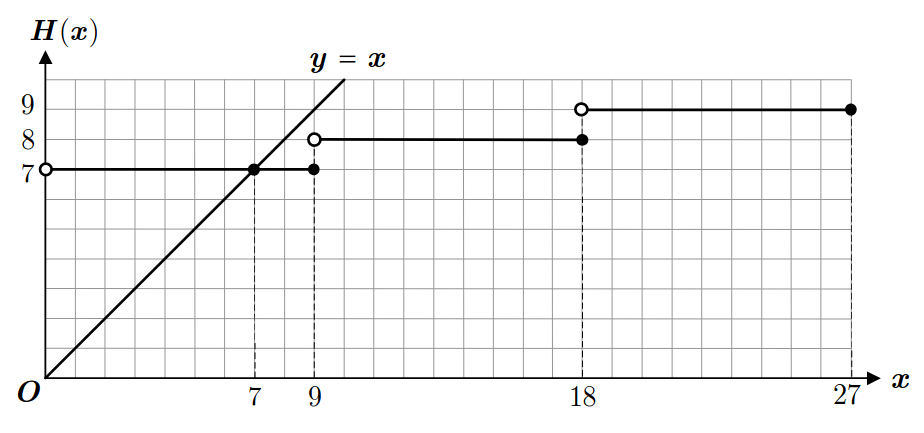
A partir del gráfico, encontramos que si \(x \in [19:27]\) entonces \(H(x)=9\) y \(H^2(x)=H(9)=7\). De manera similar, si \(x \in [10:18]\) entonces \(H^2(x)=H(8)=7\) y si \(x \in [1:9]\) entonces \(H(x)=7\).

En cualquier caso son necesarias dos iteraciones como máximo.