Cómo traducir turnpike
El término turnpike tiene varios significados. Los dos más importantes son los siguientes:

1 – En Inglés Británico, un turnpike (o turnpyke) es una barrera con púas o pinchos, diseñada para bloquear el paso de un camino o carretera a un viandante hasta que una tarifa sea satisfecha. También se denomina turnpike a todo camino dotado de tales barreras. La versión contemporánea del antiguo turnpike es el torniquete (turnstile en inglés).
2 – En Inglés Americano, un turnpike es una autopista, es decir, una carretera de larga longitud por la que generalmente circulan vehículos a gran velocidad y donde existen estaciones de peaje.
En Estados Unidos, se habla con frecuencia de algunas autopistas de gran relevancia por las ciudades que conectan y el tráfico que soportan: la New Jersey Turnpike, la Connecticut Turnpike, etc. También se conoce coloquialmente como «La Turnpike» a una banda de música country originaria de Oklahoma, la Turnpike Troubadours, fundada en 2005.
En el ámbito de la Economía, el término fue adoptado por L.W. McKenzie en los 80, haciendo referencia a las ideas de J. von Neumann y P. Samuelson, para describir una estrategia muy particular: para conseguir los mejores beneficios, es conveniente elegir medidas que puedan ser mantenidas en el tiempo y produzcan resultados de manera constante, al ritmo adecuado.
Esta idea, que ha dado excelentes resultados en Economía, subsiste en el comportamiento de muchos sistemas de la Naturaleza y, por otra parte, también ha sido aplicada con éxito en muchos otros campos. Podemos dar muchos ejemplos:
– La política educativa de un país que se precie se basa en medidas perdurables.
– La evolución de la población de un hábitat, actuando en beneficio propio, suele ser obediente a estas reglas.

– Con frecuencia, las mejores estrategias terapéuticas que se aplican en Medicina reposan sobre una intervención lenta pero constante, que produce cambios estables.
En el terreno científico, también han ganado popularidad y eficiencia estrategias y métodos basados en este principio. En particular, esto se observa con claridad cuando se diseñan técnicas que pretenden actuar sobre un sistema físico a la búsqueda de resultados óptimos.
La propiedad turnpike en problemas de control
El último aserto de la sección anterior, re-escrito en términos matemáticos, nos dice que el concepto turnpike es útil en la resolución de problemas de control. Esto ha sido analizado con intensidad por varios especialistas, muy especialmente por E. Zuazua en varios trabajos recientes.
Una situación concreta, tomada de [1], que ilustra bien la conveniencia de aplicar esta estrategia aparece cuando se planifica un viaje entre dos puntos distantes. Está claro que la mejor manera de proceder, aquélla que nos permite llegar gastando un mínimo de combustible y tal vez en el menor tiempo posible, consiste en:
a) Tomarse el trabajo de desplazarse hasta una red de autopistas que lleve a un punto cercano al deseado.
b) Realizar la mayor parte del trayecto circulando a gran velocidad (constante) por la mencionada red.
c) Finamente, acceder desde una salida de la autopista al punto de llegada.
En términos matemáticos, esta propiedad puede ser estudiada haciendo lo siguiente:

1 – Se formulan dos problemas de control óptimo: uno correspondiente al fenómeno evolutivo bajo consideración y otro asociado al fenómeno estacionario límite. Recuérdese que, en cada uno de ellos debe aparecer el control (un dato a precisar en el sistema que gobierna el fenómeno) y el estado (la solución del mismo).
2 – Se resuelven ambos problemas y se caracterizan las soluciones (los controles y estados óptimos) de la manera habitual.
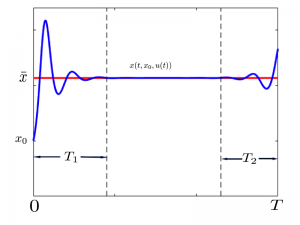
3 – Se investiga si la diferencia «control-estado evolutivo menos control-estado estacionario» es pequeña en el intervalo temporal con la posible excepción de un reducido subintervalo al comienzo y otro al final.
Este programa ha sido aplicado a un buen número de problemas de control gobernados por EDOs y EDPs. Por ejemplo, en [2], la técnica se aplica a un sistema de tipo Lotka-Volterra. Los resultados permiten mejorar las técnicas de disparo para la resolución numérica.
Para saber más
A continuación, indicaremos qué se puede hacer en este contexto cuando el modelo corresponde a una EDP lineal.
Por simplicidad, consideremos la evolución del calor en una barra de longitud \(L\) durante el intervalo de tiempo
\([0,T]\). Se supone que una fuente de calor \(v = v(x,t)\) actúa sobre los puntos de la barra situados entre \(L/4\) y \(3L/4\), la temperatura \(y = y(x,t)\) obedece a la ecuación del calor
$$
y_t – y_{xx} = v 1_{(L/4,3L/4)}
$$
(donde \(1_{(L/4,3L/4)}\) denota la función característica del intervalo espacial \((L/4,3L/4)\)), se mantiene igual a \(0\) en los extremos
$$
y(0,t) = y(L,t) = 0, \ \ t \in (0,T)
$$
y «arranca» de la temperatura inicial \(y_0\):
$$
y(x,0) = y_0(x), \ \ x \in (0,L) .
$$
Nuestro objetivo es conducir el sistema en el tiempo \(T\) a una temperatura próxima a la deseada \(y_d = y_d(x)\) aplicando una fuente \(v\) adecuada. Resulta entonces natural considerar el siguiente problema de control, denominado en lo sucesivo \(P_1\):
$$
\left\{
\begin{array}{l} \displaystyle
\hbox{Minimizar } \frac{1}{2} \int_0^L |y(x,T) – y_d(x)|^2 \,dx
+ \frac{1}{2} \int_0^T \!\!\! \int_{L/4}^{3L/4} |v(x,t)|^2 \,dx\,dt
\\ \displaystyle
\hbox{Sujeto a } v \in U, \ \ y \ \hbox{solución asociada,}
\end{array}
\right.
$$
donde \(U\) es el espacio adecuado de controles: \(U = L^2((L/4,3L/4) \times (0,T))\).

Consideremos ahora la situación «ideal» en la que el sistema está en estado estacionario, es decir, la temperatura \(\overline{y} = \overline{y}(x)\) y la fuente de calor \(\overline{v} = \overline{v}(x)\) verifican
$$
– \overline{y}_{xx} = \overline{v} 1_{(L/4,3L/4)} ,
$$
y las igualdades
$$
\overline{y}(0) = \overline{y}(L) = 0 .
$$
Tiene perfecto sentido considerar el nuevo problema de control \(P_2\):
$$
\left\{
\begin{array}{l} \displaystyle
\hbox{Minimizar } \frac{1}{2} \int_0^L |\overline{y}(x) – y_d(x)|^2 \,dx
+ \frac{1}{2} \int_{L/4}^{3L/4} |\overline{v}(x)|^2 \,dx
\\ \displaystyle
\hbox{Sujeto a } \overline{v} \in \overline{U}, \ \ \overline{y} \ \hbox{solución asociada,}
\end{array}
\right.
$$
donde \(\overline{U} = L^2(L/4,3L/4)\).
Es relativamente sencillo demostrar que ambos problemas, \(P_1\) y \(P_2\), poseen solución única. El carácter «turnpike» de la solución de \(P_1\) queda probado en el siguiente resultado de [3]:
Teorema: Sea \(v\) (resp. \(\overline{v}\)) la solución de \(P_1\) (resp. \(P_2\)) y sea \(y\) (resp. \(\overline{y}\)) la temperatura asociada. Entonces existen \(C, \lambda > 0\) y \(T_0 > 0\) tales que, si \(T > T_0\), se tiene
$$
\int_{L/4}^{3L/4} |v(x,t) – \overline{v}(x)|^2 \,dx + \int_0^L |y(x,t) – \overline{y}(x)|^2 \,dx
\leq C \left( e^{-2\lambda t} + e^{-2\lambda(T-t)} \right).
$$
Un resultado análogo se puede demostrar para muchos otros sistemas. Un buen número de ellos aparece en [4,5,6] y en las referencias allí mencionadas, acompañados de numerosos comentarios y problemas abiertos.
Referencias
[1] E. Zuazua, La teoría de la autopista o del «turnpike», DEIA, 29 de Julio de 2016.
[2] A. Ibáñez, Optimal control of the Lotka-Volterra system: turnpike property and numerical simulations. Journal of Biological Dynamics, 11(1): 25-41, 2017.
[3] A. Porretta, E. Zuazua, Long time versus steady state optimal control. SIAM Journal on Control and Optimization, 51(6): 4242-4273, 2013.
[4] E. Trélat, E. Zuazua, The turnpike property in finite-dimensional nonlinear optimal control. Journal of Differential Equations, 258(1): 81-114, 2015.
[5] B. Geshkovski, E. Zuazua, Turnpike in optimal control of PDEs, ResNets, and beyond. Acta Numer. 31 (2022), 135-263.
[6] T. Faulwasser, L. Grüne, Turnpike properties in optimal control. An overview of discrete-time and continuous-time results. Numerical control. Part A, 367-400, Handb. Numer. Anal., 23, North-Holland, Amsterdam, 2022.

Dejar una contestacion