Nash
John Forbes Nash (1928-2015) fue un matemático estadounidense, especialista en teoría de juegos, geometría diferencial y ecuaciones en derivadas parciales, laureado con el Premio Nobel de Economía en 1995 y con el Premio Abel en 2015.
Se licenció en Matemáticas en 1948 en la Universidad Carnegie Mellon y se trasladó a continuación a la Universidad de Princeton para iniciar su doctorado. En 1949 escribió un artículo titulado Puntos de equilibrio en juegos de \(n\)-personas, en el que definía el equilibrio de Nash. Con sólo 21 años, se doctoró con una Tesis de menos de treinta páginas sobre juegos no cooperativos, bajo la dirección de Albert W. Tucker y consiguió inmediatamente reconocimiento entre el resto de los especialistas; véase [1].

En 1950 empezó a trabajar para la RAND Corporation, institución que canalizaba fondos del Gobierno de los Estados Unidos para estudios científicos relacionados con la guerra fría. Posteriormente, fue profesor en el Massachusetts Institute of Technology de 1952 a 1955 y en la Universidad de Princeton, de 1955 en adelante.
Se casó en 1957 con una ex-alumna suya del MIT, Alicia Lardé López-Harrison, con quien tuvo un hijo, John Charles Martin Nash. Tras un año de matrimonio se le diagnosticó esquizofrenia. Inicialmente, la enfermedad mental de Nash se manifestó como paranoia. Nash parecía creer que todos los hombres que usaban corbatas rojas formaban parte de un grupo de comunistas que conspiraban contra él; incluso envió cartas a las embajadas en Washington, D.C., afirmando que ellos estaban estableciendo una especie de gobierno paralelo en el país.
Sus problemas psíquicos comenzaron a afectar a su vida profesional cuando, en una de sus conferencias sobre la hipótesis de Riemann, leído en la Universidad de Columbia en 1959, Nash se expresó con palabras que resultaron incomprensibles.
En 1961 ingresó al Hospital Psiquiátrico de Trenton, en Nueva Jersey. Y durante los nueve meses siguientes pasó períodos en varios hospitales psiquiátricos, en los que recibió tratamientos con fármacos anti-psicóticos y terapias de shock con insulina.
Según su biógrafa Sylvia Nasar, Nash se recuperó gradualmente de su enfermedad con el paso del tiempo y gracias al apoyo de su esposa y logró seguir trabajando gracias a su entorno comunitario, en donde se aceptaban sus excentricidades. Nash sugirió que sus delirios estaban relacionados con su sensación de infelicidad, a sus deseos de sentirse importante y reconocido y a su forma característica de pensar, diciendo: «Yo no habría tenido ideas tan buenas científicamente, si hubiera tenido una forma más normal de pensar». También expresó: «Si no me hubiera sentido tan presionado, dudo que hubiera sufrido este trastorno».
Sus contribuciones han influido en las negociaciones comerciales globales, en los avances de la biología evolutiva y en las relaciones laborales nacionales, véase [2]. En particular, en el ámbito de la teoría económica, Nash introdujo el concepto de equilibrio que lleva su nombre: un equilibrio de Nash es aquél en el que \(n\) actores que actúan de forma independiente son sin embargo capaces de coexistir y optimizar \(n\) beneficios distintos.
Nash falleció a los 86 años junto a su esposa Alicia, de 82, el 23 de mayo de 2015, en el viaje de regreso tras haber recibido el Premio Abel 2015 de manos del rey Harald V, en Oslo. El suceso se produjo en el peaje de la New Jersey Turnpike, cerca de Monroe Township, Nueva Jersey. El conductor del taxi en el que venían del aeropuerto de Newark perdió el control y golpeó una barandilla. La colisión se produjo cuando el taxi intentó adelantar a otro vehículo. Según la policía local, ninguno de los Nash llevaba puesto el cinturón de seguridad, por lo que la pareja salió despedida del vehículo tras el impacto.
La película de 2001 A Beautiful Mind, ganadora de cuatro Oscars (entre ellos el de Mejor Película), está basada en su vida a partir de la novela homónima de Sylvia Nasar.
Pareto

Vilfredo Federico Pareto (1848-1923), fue un ingeniero, economista y sociólogo italiano. Se doctoró en Ingeniería en 1869 en el Instituto Politécnico de Turín. Desde muy pronto, demostró una formación muy completa en Matemáticas y en cultura humanística. Estas cualidades le permitieron simultáneamente ejercer como hombre de empresa y analizar con profundidad el devenir económico de la sociedad.
Fue durante mucho tiempo director y administrador de varias compañías y, entre 1893 y 1906, profesor de Economía Política en la Universidad de Lausanne. Así, la naturaleza de la actividad que desempeñó le generó gran interés por las teorías económicas, a las que contribuyó con gran cantidad de aportaciones y varios libros en un intento exitoso de dar fundamento científico.
En 1906 se retiró a Céligny, en el cantón de Ginebra, a un tranquilo poblado llamado Villa Angora, donde dedicó el último período de su vida al estudio. Allí publicó sus trabajos más conocidos: el Manual de Economía Política y el Tratado de Sociología; véanse [3, 4].
En 1906 hizo la famosa observación de que el 20 % de la población poseía el 80 % de la propiedad en Italia, posteriormente generalizada por Joseph M. Juran en el llamado Principio de Pareto, también conocido como la Regla del 80-20. En 1909, introdujo el índice de Pareto, una medida de la desigualdad de la distribución de la renta y las curvas de indiferencia, que se interpretan como aquellos conjuntos de bienes donde un consumidor se siente indiferente.
Finalmente, continuando la obra del economista Walras, introdujo el concepto de óptimo de Pareto; véase [5]. Postuló que, en un sistema económico, se debe llegar a una situación tal que todos los consumidores y todos los agentes productores y ofertantes son incapaces de mejorar su estado sin perjudicar el de otro.
Los equilibrios y su significado
Para comprender bien de lo que estamos hablando supongamos dadas dos funciones convexas y diferenciables
$$
J_i : {\bf R}^2 \mapsto {\bf R} , \ \ i = 1,2
$$
y supongamos que se desea que ambas funciones tomen valores tan pequeños como sea posible.
Obviamente, estos deseos pueden entrar en conflicto, por lo que parece oportuno buscar una especie de compromiso, esto es, un punto \((u_1,u_2)\) tal que los valores \(J_1(u_1,u_2)\) y \(J_2(u_1,u_2)\) nos dejen satisfechos.
Por definición, un equilibrio de Nash es un par \((u_1,u_2)\) que verifica
$$
\left\{
\begin{array}{l}\displaystyle
J_1(u_1,u_2) \leq J_1(v_1,u_2) \quad \forall v_1 \in {\bf R} ,
\\ \displaystyle
J_2(u_1,u_2) \leq J_2(u_1,v_2) \quad \forall v_2 \in {\bf R} .
\end{array}
\right.
$$
En un equilibrio de Nash, las componentes \(u_1\) y \(u_2\) actúan independientemente, de manera que cada una se ocupa de una y sólo una de las funciones \(J_i\). Se dice entonces que estamos ante un equilibrio no cooperativo.
Por otra parte, diremos que \((u_1,u_2)\) es un equilibrio de Pareto si
$$
\left\{
\begin{array}{l}\displaystyle
\not\exists (v_1,v_2) \in {\bf R}^2 \ \hbox{ tal que para } i = 1,2
\\ \displaystyle
J_i(v_1,v_2) \leq J_i(u_1,u_2) , \hbox{ con alguna desigualdad estricta.}
\end{array}
\right.
$$
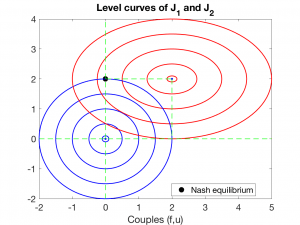
Luego, contrariamente a lo anterior, en un equilibrio de Pareto, las componentes \(u_1\) y \(u_2\) actúan de manera coordinada. Se dice que el equilibrio es cooperativo.
Naturalmente, en ambos casos tiene perfecto sentido considerar equilibrios sujetos a restricciones.
Gracias a la convexidad y diferenciabilidad de \(J_1\) y \(J_2\), es fácil caracterizar los equilibrios de Nash y de Pareto. Así, \((u_1,u_2)\) es un equilibrio de Nash si y sólo si
$$
\partial_i J_i(u_1,u_2) = 0, \quad i = 1,2.
$$
Por otra parte, \((u_1,u_2)\) es un equilibrio de Pareto si y sólo si
$$
\exists \alpha \in [0,1] \ \hbox{ tal que } \ \alpha J_1′(u_1,u_2) + (1-\alpha) J_2′(u_1,u_2) = 0.
$$
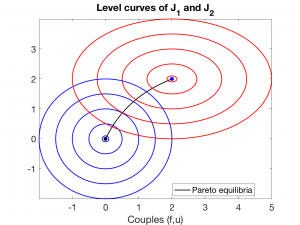
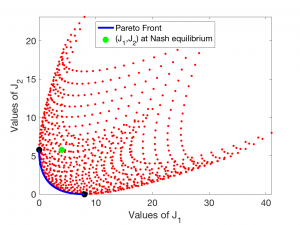
En el contexto de los equilibrios de Pareto, es muy intuitivo considerar el frente de Pareto. Se trata de la curva del plano que une los puntos
$$
(J_1(u_1,u_2),J_2(u_1,u_2)) , \ \hbox{ donde $(u_1,u_2)$ es un equilibrio de Pareto.}
$$
Algunas aplicaciones
Hay una larga lista de áreas de trabajo donde la optimización multi-criterio en general y los conceptos de equilibrio en particular son aplicables. Destacaremos a continuación algunas de ellas.
Economía
Muchos problemas económicos hacen aparecer de manera natural varios objetivos junto con restricciones que indican que combinaciones de estos objetivos deben ser alcanzables.
Por ejemplo, la demanda de consumo de varios bienes distintos suele estar determinada por un proceso en donde maximizamos la utilidad de cada uno de ellos, sujeta a restricciones basadas en cuánto podemos pagar por su adquisición y qué precio poseen. Lógicamente, los distintos objetivos (los distintos niveles de consumo) pueden estar en conflicto entre sí.
Por otro lado, la política macro-económica de un país (o de una organización como la Unión Europea) es, esencialmente, optimización multi-objetivo. Típicamente, un Banco Central debe elegir una política monetaria que permita equilibrar o compensar varios objetivos: menos inflación, menos desempleo, menos déficit en la balanza de pagos, etc. Para ello, el Banco se ve obligado a utilizar un modelo que describa cuantitativamente y de manera combinada los distintos elementos económicos y calcular uno o varios equilibrios.
Finanzas
Aquí, un problema común consiste en diseñar una estrategia de gestión de cartera en presencia de dos o más objetivos en conflicto. En efecto, siempre es deseable tener un rendimiento de la cartera tan alto como sea posible y, al mismo tiempo, un nivel de riesgo tan pequeño como se pueda. Una vez cuantificados el rendimiento y el riesgo, se acepta con frecuencia que la solución a este problema viene dada por el correspondiente frente de Pareto.
Control óptimo
En muchos problemas con origen en Ingeniería se pretende optimizar distintos aspectos del producto que pueden ser contradictorios y difíciles de jerarquizar. Por ejemplo, en sistemas de generación de energía puede no estar claro en absoluto si priorizar rendimiento o coste. A menudo, estos problemas son descritos a partir de varias funciones de coste que dependen de varios datos (los controles) y de las soluciones asociadas de un sistema de ecuaciones (los estados). La existencia y análisis de equilibrios es la vía natural de resolución en muchos casos.
Mantenimiento de infraestructuras
El mantenimiento e inspección de infraestructuras es esencial para reducir costes de producción, riesgos de mal funcionamiento, impacto medioambiental, etc. Para estructuras complejas, el plan diseñado debe ser concebido en el ámbito multi-objetivo, a la vez maximizando la cobertura de análisis y minimizando tiempo y costes.
Para saber más. Control óptimo bi-objetivo
Consideraremos un problema de control óptimo bi-objetivo relacionado con el uso combinado de terapias anticancerígenas.
El modelo elegido es relativamente sencillo: un SDO con interacción competitiva donde aparecen dos controles (\(v\) y \(w\)), respectivamente relacionados con estrategias de radioterapia y quimioterapia. Resulta natural considerar controles en el espacio \(L^2(0,T)\). La solución del SDO se compone de las funciones \(y = y(t)\) y \(z = z(t)\), que respectivamente determinan las densidades normalizadas de células cancerígenas y anticuerpos generados en el organismo.
Así, supondremos que
\[
\left\{
\begin{array}{l}\displaystyle
y_t = \rho y (1-y) – zy – v(t) y , \ \ t \in (0,T),
\\ \displaystyle
z_t = – K z + w(t) , \ \ t \in (0,T),
\\ \displaystyle
y(0) = y_0, \ \ z(0) = z_0 ,
\end{array}
\right.
\]
consideraremos las funciones de coste
$$
J_1(v,w) := \frac{1}{2} |y(T)|^2 + \frac{\mu}{2} \int_0^T |v(t)|^2 \,dt
$$
y
$$
J_2(v,w) := \frac{1}{2} \int_0^T |z(t) – z_d|^2 \,dt + \frac{\mu}{2} \int_0^T |w(t)|^2 \,dt
$$
y buscaremos un equilibrio de Nash asociado.
En este contexto, las funciones \(J_1\) y \(J_2\) son diferenciables pero no convexas en \(L^2(0,T) \times L^2(0,T)\).
Por tanto, resulta más complicado determinar equilibrios de Nash. Sin embargo, sí es relativamente sencillo calcular quasi-equilibrios de Nash, es decir, pares \((v,w)\) tales que
$$
\partial_1 J_1 (v,w) = 0 \ \hbox{ y } \ \partial_2 J_2 (v,w) = 0 .
$$
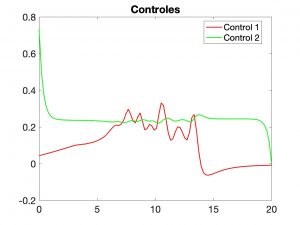
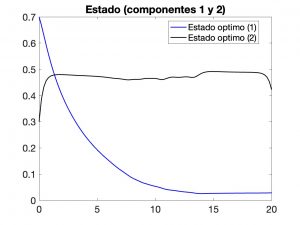
En las Figuras 6 y 7 hemos visualizado aproximaciones numéricas de un quasi-equilibrio y de la correspondiente solución \((y,z)\) para \(z_d = 1/2\) y \(\mu = 0.1\). Se observa que, con las técnicas aplicadas, es posible determinar controles que hacen \(y(T)\) pequeño y \(z(t)\) próximo a \(z_d\). Para más detalles sobre el tratamiento de problemas de control multi-objetivo, véase por ejemplo [6].
Referencias
-
J. Nash, Non-Cooperative Games, Annals of Mathematics, Vol. 54 (1951), pp. 286-295.
-
T. Siegfried, A Beautiful Math: John Nash, Game Theory, and the Modern Quest for a Code of Nature, National Academies Press, 2006.
-
V. Pareto, Manuale di economia politica – con una introduzione alla Scienza Sociale, Milano, 1906 (reimpresión 1919).
-
V. Pareto, Trattato di Sociologia generale, Firenze, 1916.
-
V. Pareto, Économie mathématique, Encyclopédie des Sciences, Mathématiques, Paris, 1911.
-
S.P. Sethi, Optimal control theory – applications to management science and economics, Fourth edition, Springer Texts in Business and Economics. Springer, Cham, 2021.

Dejar una contestacion