En esta entrada hablaremos sobre las personalidades de Erwin Schrödinger y Paul Dirac. Ya han aparecido sus contribuciones en varias entradas anteriores. Ya somos conscientes de su relevancia en la Física. Ahora aprenderemos algo sobre sus vidas personales.
Para empezar, una anécdota sobre otro genio. Lector, a ver si sabes de quién se trata:
Un día Ernest Rutherford, Premio Nobel de Química, pidió a un alumno en un examen que le mostrara cómo es posible determinar la altura de un edificio con la ayuda de un barómetro.

El alumno respondió: «Muy fácil; lleve el barómetro a la azotea del edificio y átele una cuerda muy larga; descuelgue hasta la base del edificio, marque y mida».
Buscando ser ecuánime, decidió volver a pedirle lo mismo, pero esta vez advirtiéndole que la respuesta debía contener argumentos propios de la Física. Tras unos minutos, el estudiante dijo que tenía varias respuestas y que no sabía cómo elegir la mejor:
-
Dejar caer el barómetro desde la azotea, calcular el tiempo de caída con un cronómetro y aplicar la fórmula \(h = \frac{1}{2} g t^2\).
-
En un día soleado, medir la altura del barómetro, la longitud de su sombra, la longitud de la sombra del edificio y aplicamos una simple proporción.
-
Atar el barómetro a una cuerda, descolgarlo hasta la calle, usarlo como un péndulo y medir el período del movimiento generado.
-
Un método muy directo: subir las escaleras marcando en la pared una y otra vez la altura del barómetro y multiplicar el número total de marcas por la altura del barómetro.
Intrigado, Rutherford preguntó al alumno si conocía la respuesta típica (la diferencia de presión marcada por el barómetro en la azotea y en la calle proporciona la diferencia de altura). Respondió que sí pero que, siguiendo el consejo de sus profesores, había decidido dar preferencia a pensar.
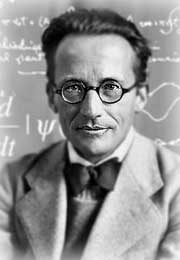
Schrödinger
Erwin Rudolf Josef Alexander Schrödinger (188-1961) fue un físico y filósofo austríaco, naturalizado irlandés, que realizó importantes contribuciones en los campos de la mecánica cuántica y la termodinámica. Recibió el Premio Nobel de Física en 1933 por haber desarrollado la ecuación que lleva su nombre, compartido con Paul Dirac.
La trayectoria académica y personal seguida por Schrödinger a lo largo de su vida no tuvo desperdicio.
Entre 1914 y 1918 participó en la I Guerra Mundial como soldado del ejército austriaco. Su actividad profesional comenzó en 1920, contratado como ayudante de Max Wien en Jena. Posteriormente, consiguió plazas de profesor asociado en Stuttgart y de profesor titular en Breslavia, Zürich y Berlin.
Abandonó Alemania en 1933 en pleno auge del antisemitismo del Partido Nazi y emigró a Austria, tras rechazar una plaza permanente en Princeton. Y posteriormente fue a Roma, de nuevo a Oxford y finalmente a Dublín, donde residió hasta su jubilación, en 1955.
La ecuación de Schrödinger, presentada en 1926 en un artículo titulado «Quantisierung als Eigenwertproblem» (Cuantización como problema de autovalores) en la revista Annalen der Physik, describe la evolución temporal de una partícula subatómica de naturaleza ondulatoria y no relativista. Es de importancia central en mecánica cuántica, jugando para las partículas microscópicas un papel análogo al de la segunda ley de Newton en mecánica clásica.
No está claro de dónde le vino a Schrödinger la idea de formular la ecuación. En dos cartas enviadas a Einstein contó a éste que la inspiración le llegó en las vacaciones de Navidad que pasó en un romántico hotel en Arosa, en plenos Alpes suizos. Curiosamente, pasó esos días en compañía de una mujer cuya identidad nunca fue revelada.
Resulta extraño que Schrödinger ocultara esa aventura, puesto que su matrimonio con Anne Marie Bertel era de carácter abierto. De hecho, ella no solo toleraba sus aventuras sino que participaba en muchas de ellas. Entre otros datos, se sabe que vivieron durante muchos años con Hilde March y que, durante ese período, Schrödinger tuvo una hija con cada una de ellas. También se sabe que Anne Marie tuvo un romance con André Weil, amigo de Schrödinger, matemático francés, uno de los miembros fundadores del grupo Bourbaki.
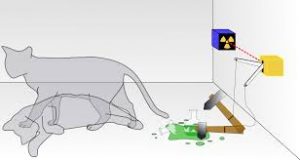
En cualquier caso, la ecuación que lleva su nombre constituyó y constituye un modelo revolucionario para la comprensión de la mecánica cuántica. Tras años de reflexión, propuso el experimento mental del gato de Schrödinger que muestra las paradojas e interrogantes a los que aboca la lógica de lo microscópico.
Schrödinger es mucho menos conocido por aportar ideas igualmente revolucionarias en Biología. Sin embargo, se puede afirmar que fue el primer científico en concebir la existencia de un «código genético», diez años antes del descubrimiento del ADN por parte de Watson y Crick.
En 1944, publicó un libro titulado «¿Qué es la vida?» (What is life?), como resultado de varias conferencias de tipo divulgativo. Ahí aparecen dos ideas fundamentales:
- La vida es información y, en consecuencia, la evolución de los sistemas biológicos respeta las leyes de la Termodinámica, es decir, conduce a un aumento de «entropía» que puede interpretarse como desorden o complejidad.
- La herencia biológica debe transmitirse sobre la base de «cristales aperiódicos», es decir, compuestos químicos de estructura regular pero no repetitiva, capaces de codificar información.
Varios años después la influencia de estas ideas en el descubrimiento de la conocida estructura de doble hélice del ADN fue reconocida por el mismo James Watson en su libro «DNA, The Secret of Life».
Schrödinger dedicó sin éxito los últimos años de su carrera científica a desarrollar una teoría del campo unificado que permitiera explicar al mismo tiempo la gravedad, el electromagnetismo y las fuerzas nucleares. Como se sabe, éste sigue siendo uno de los grandes retos pendientes de la Física.

Dirac
Paul Adrien Maurice Dirac (1902-1984) fue un ingeniero eléctrico, matemático y físico teórico británico. Contribuyó de manera fundamental al desarrollo de la mecánica cuántica.
Ocupó la Cátedra Lucasian de Matemáticas de la Universidad de Cambridge, aunque posteriormente emigró a Estados Unidos, estableciéndose en la Universidad Estatal de Florida. Entre otros descubrimientos formuló la ecuación que lleva su nombre, que describe el comportamiento de los fermiones. Esto le permitió predecir la existencia de la antimateria.
Dirac describió su infancia como infeliz, por la severidad y autoritarismo de su padre. Una reciente biografía ha matizado tal carácter, haciendo referencia al propio carácter difícil y taciturno de Paul.
Se graduó en Ingeniería Eléctrica en la Universidad de Brístol en 1921 y de hecho trabajó durante algún tiempo como ingeniero pero posteriormente decidió que su verdadera vocación eran las Matemáticas. Dos años después era graduado por Matemáticas en Brístol y fue entonces admitido en la Universidad de Cambridge, donde desarrollaría la mayor parte de su carrera. Allí trabajó bajo la supervisión de Ralph Fowler, iniciándose en física cuántica.
En 1926 completó un modelo de mecánica cuántica que unificaba las ideas de Heisenberg y de Schrödinger identificando cantidades medibles con operadores en espacios de Hilbert. Dos años después, dedujo la ecuación de Dirac, una ecuación relativista que describe el comportamiento del electrón. Este trabajo permitió a Dirac predecir la existencia del positrón (la antipartícula del electrón), que fue observado por primera vez por Carl Anderson en 1932. Dirac contribuyó también a explicar el spin como un fenómeno relativista.
Dirac era conocido entre sus colegas como un tipo raro, muy preciso en sus afirmaciones y también seco y taciturno. Las anécdotas sobre su tendencia al silencio se hicieron famosas. Se acuñó una unidad, el «dirac», para la cantidad mínima de palabras que se podían decir en una conversación. En su biografía «The strangest man», de Graham Farmelo, se sugiere que tenía síndrome de Asperger, ya que su lenguaje era lacónico y literal y no solía hablar mucho con los demás.
Muchos físicos consideran que Dirac fue un genio, sólo comparable a Einstein o Feynman. Que sea tan poco conocido es tal vez consecuencia de su personalidad. Mientras Einstein y Feynmann tenían mucho de estrellas mediáticas, Dirac no soportaba la publicidad ni mostró jamás interés por la difusión de sus trabajos más allá del círculo especializado en el que se movió.
Para saber más: las ecuaciones
La ecuación de Schrödinger
La forma concreta de la ecuación de Schrödinger depende de la situación física. En su versión más conocida, la ecuación dice lo siguiente:
$$
ih \, \psi_t – H\psi = 0 ,
$$
donde \(i\) es la unidad imaginaria, \(h\) es la constante de Planck reducida (dividida por \(2\pi\)), el subíndice \(t\) indica una derivada parcial con respecto al tiempo, \(\psi = \psi(x,t)\) es la función de onda del sistema cuántico y \(H\) es el operador Hamiltoniano (un operador en derivadas parciales espaciales de segundo orden determinado por la energía presente en el sistema que tiene diferentes formas dependiendo de la situación considerada).
Así, en el caso de una partícula simple sometida a los efectos de un campo eléctrico, tenemos
$$
H\psi = -\frac{h^2}{2\mu} \Delta\psi + V\psi ,
$$
donde \(\mu\) es una constante proporcional a la masa de la partícula y \(V = V(x,t)\) es el potencial eléctrico del campo.
Si se admite que la partícula bajo estudio puede moverse (por ejemplo) en el abierto acotado no vacío \(\Omega \subset {\bf R}^N\) durante el intervalo de tiempo \((0,T)\), la ecuación debe ser resuelta en \(\Omega \times (0,T)\), completada con condiciones de contorno sobre \(\partial\Omega \times (0,T)\) y condiciones iniciales en \(\Omega\) para \(t = 0\).
Sea \(\psi\) la solución. Fijados un conjunto medible \(G \subset \Omega\) y un instante \(\overline{t}\), se interpreta que la probabilidad de que la partícula esté en \(G\) en el tiempo \(\overline{t}\) está dada por
$$
\hbox{P}_\psi(G;\overline{t}) = \int_G |\psi(x,\overline{t})|^2 \,dx .
$$
La ecuación de Dirac
Esta ecuación describe el comportamiento de una partícula elemental en mecánica cuántica relativista. Debe ser consistente con los principios de la mecánica cuántica y de la relatividad especial, lo cual la hace mucho más complicada.
Presenta la siguiente forma:
$$
ih \Psi_t = \mathbf{H} \Psi ,
$$
donde ahora la «función de onda» \(\Psi\) posee cuatro componentes y el operador \(\mathbf{H}\) actúa de la forma siguiente
$$
\mathbf{H} \Psi = \left(\mu c^2 \alpha_0
– ih \sum_{j=1}^3 \alpha_j \partial_j\right) \Psi ,
$$
donde las \(\alpha_j\) son las llamadas matrices de Dirac.
De nuevo, la resolución de la ecuación (convenientemente complementada con condiciones de contorno e iniciales) proporciona la probabilidad de encontrar la partícula en una región prefijada arbitrariamente en un tiempo dado. Muchas otras características del estado cuántico de la partícula pueden ser también obtenidas a partir de \(\Psi\).
Para saber más: algunas referencias
- Berezin, F. A. ; Shubin, M. A. The Schrödinger equation. Mathematics and its Applications (Soviet Series), 66. Kluwer Academic Publishers Group, Dordrecht, 1991.
- Pankov, A. Lecture notes on Schrödinger equations. Contemporary Mathematical Studies. Nova Science Publishers, Inc., New York, 2007.
- Schrödinger, E. What is life? (with Mind and Matter & Autobiographical Sketches). Cambridge University Press, New York, 1992.
- Thaller, B. The Dirac equation. Texts and Monographs in Physics. Springer-Verlag, Berlin, 1992.

De dónde le vino a Schrödinger la idea de formular su ecuación lo cuenta Felix Bloch en el siguiente artículo:
F. Bloch, Heisenberg and the early days of quantum mechanics, Phys. Today, 29, 23-27, 1976.