Publicamos la solución al divertimento Coordenadas triangulares. En esta ocasión hemos recibido respuestas acertadas de Anónimo17, Renato Álvarez y Niurka Rodríguez, F. Damián Aranda y Antonio Medinilla y David Ramos.
Divertimento:
Sea un triángulo \(ABC\) y denotemos por \(p\) a su semiperímetro. Partiendo desde \(A\) recorremos el lado \(AB\) y llegamos a un punto \(P\) en \(BC\) de modo que la distancia recorrida sea \(p\). Luego partimos de \(B\), recorremos \(BC\) y llegamos a un punto \(Q\) en \(CA\) tal que la distancia recorrida desde \(B\) sea \(p\). Y, por último, partimos de \(C\), recorremos \(CA\) y llegamos a \(R\), situado en \(AB\), tal que la distancia recorrida desde \(C\) sea \(p\). Se pregunta si las rectas \(AP\), \(BQ\) y \(CR\) son concurrentes. Como los procedimientos habituales para quienes no sean especialistas en la geometría del triángulo pueden resultar algo intrincados, proponemos resolverlo mediante un sistema de referencia que pasamos a describir. Consideremos el triángulo \(ABC\). Dado un punto \(P\) cualquiera del plano, consideremos las distancias de dicho punto a las rectas \(BC\), \(AC\) y \(AB\), asignando a dichos números el signo \(+\) o \(-\) según que el punto \(P\) se encuentre en el mismo o distinto semiplano que el triángulo con respecto a dichas rectas. Denotemos por \((\alpha,\beta,\gamma)\) a estos números con signo. Diremos que las coordenadas de \(P\) son \([\alpha:\beta:\gamma]\) o \([k\alpha:k\beta:k\gamma]\) para cualquier \(k\) real positivo. Así, por ejemplo, diremos que las coordenadas del incentro del triángulo, punto equidistante de los lados, son \([1:1:1]\), y pueden nuestros lectores entretenerse en comprobar que las coordenadas triangulares del baricentro de \(ABC\) son \(\displaystyle{\left[\frac{1}{a}:\frac{1}{b}:\frac{1}{c}\right]}\) Es evidente que cada punto tiene una terna de coordenadas y que no existe ningún punto con las tres coordenadas negativas. Puede probarse que la ecuación de la recta que pasa por dos puntos \(A=(\alpha_1,\alpha_2,\alpha_3)\) y \(B=(\beta_1,\beta_2,\beta_3)\) es $$\left|\begin{array}{ccc} x&y&z\\ \alpha_1 & \alpha_2 & \alpha_3 \\ \beta_1 & \beta_2 & \beta_3 \\ \end{array}\right|=0.$$ Usando todo lo anterior, os pedimos contestar a la pregunta planteada en el primer párrafo, indicando, en caso afirmativo, las coordenadas del punto de concurrencia en función de las longitudes de los lados de \(ABC\).
Solución:
Varios de nuestros lectores han utilizado el Teorema de Ceva para garantizar la concurrencia de las rectas. Nosotros utilizaremos la expresión indicada en el enunciado del problema para la recta que pasa por dos puntos dados. El punto \(P\) situado en el lado BC, tal que \(AB+BP=p\), tiene de coordenadas $$P=[0:(p-b)\sin(C):(p-c)\sin(B)],$$ de modo que la recta AP tiene de ecuación $$\left|\begin{array}{ccc} x&y&z\\ 1 & 0 & 0 \\ 0&(p-b)\sin(C) & (p-c)\sin(B) \\ \end{array}\right|=0,$$ o equivalentemente, $$AP: (p-c)\sin(B)y-(p-b)\sin(C)z=0.$$ Análogamente, las ecuaciones de las rectas BQ y CR son $$BQ: (p-c)\sin(A)x-(p-a)\sin(C)z=0$$ $$CR: (p-b)\sin(A)x-(p-a)\sin(B)y=0.$$ 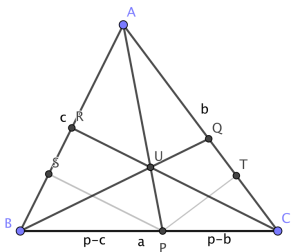 Y estas tres rectas pasan por el punto $$U=\left[\frac{p-a}{\sin(A)}:\frac{p-b}{\sin(B)}:\frac{p-c}{\sin(C)}\right],$$ o si se prefiere, utilizando el Teorema del Seno, $$U=\left[\frac{p-a}{a}:\frac{p-b}{b}:\frac{p-c}{c}\right].$$
Y estas tres rectas pasan por el punto $$U=\left[\frac{p-a}{\sin(A)}:\frac{p-b}{\sin(B)}:\frac{p-c}{\sin(C)}\right],$$ o si se prefiere, utilizando el Teorema del Seno, $$U=\left[\frac{p-a}{a}:\frac{p-b}{b}:\frac{p-c}{c}\right].$$

Dejar una contestacion