Publicamos la solución al divertimento Un problema sin reglas. Muchas gracias a Renato Álvarez y Niurka Rodríguez, Anónimo17, F. Damián Aranda, Don Diedro y Don Pablo y Magdalena Jáñez por mandarnos sus propuestas de solución.
Divertimento:
Como todos los lunes, la profesora de dibujo, apodada cariñosamente por su alumnado La Escuadra, puso una prueba corta de diez minutos al comienzo de la clase. Uno de sus alumnos, Jimeno, de nombre de usuario Jimo, había estado participando activamente en una discusión por la red social mientras preparaba la mochila la tarde anterior y se dejó en su casa la bolsa de las reglas, cogiendo solo el compás que llevaba en el estuche de bolígrafos y lápices. El problema a resolver era que se dibujara una circunferencia y se dividiera en cuatro arcos iguales.
¿Podrá presumir Jimo en la red social de haber resuelto el problema de La Escuadra sin regla?
Solución:
Sea \(r\) el radio de la circunferencia de centro \(O\). Tomando un punto \(A\) de la circunferencia, se puede llevar el radio tres veces sobre ella obteniendo tres arcos \(AB\), \(BC\) y \(CD\) respectivamente. De este modo, se cumple que \(A\) y \(D\) son los extremos de un diámetro, puesto que el lado del hexágono regular es igual al radio. Con este paso, los puntos \(A\) y \(D\) dividen la circunferencia en dos arcos iguales. Vamos a llamar \(P\) al punto medio del arco \(AD\) que estamos buscando.
Ahora bien, el segmento \(AC\) es la diagonal del hexágono regular cuya longitud es \(r \sqrt{3}\) según el Teorema del Coseno. De modo que, \(E\), que es el punto de intersección de las circunferencias de centros \(A\) y \(D\) respectivamente y de radio \(r\sqrt{3}\), es el punto de la mediatriz de \(AD\) que está a dicha distancia de \(A\) y \(D\). Del Teorema de Pitágoras se deduce que las distancias \(OE\) y \(AP\) es \(r\sqrt{2}\). Por tanto, el punto \(P\) (y el \(P’\)) se obtienen como puntos de intersección de la circunferencia dada con la circunferencia de centro \(A\) y radio \(OE\).
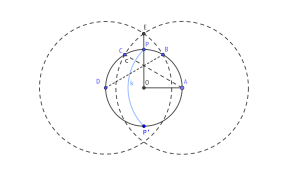
Este problema es conocido como Problema de Napoleón.

Dejar una contestacion