La topología aplicada ha vuelto a resurgir con una fuerza inusitada, esta vez en el campo de la neurociencia. Concretamente, en el proyecto Blue Brain ([1]) en Laussane (Suiza), técnicas de reconstrucción simplicial y cálculo homológico se aplican al modelado de redes de activación neuronal en el cerebro o dicho de otra forma, al procesado cerebral de información cuando se le expone a un estímulo.
¿En qué consiste la propuesta de estos investigadores del proyecto Blue Brain ([1])?
Cuando un cerebro es expuesto a un estímulo, las neuronas aparentemente se activan aleatoriamente. Podemos detectar esta activación, que crece hasta un cierto momento, para después decrecer rápidamente, y crear un video de activación neuronal para análisis de la misma. Por ejemplo, la comunicación sináptica a nivel químico fluye desde una neurona a otra y se puede describir esta información dibujando un grafo dirigido, cuyos nodos son las neuronas y cuyas aristas dirigidas son los posibles flujos entre ellas.
En esta imagen, los flujos más recientes se muestran como más brillantes:
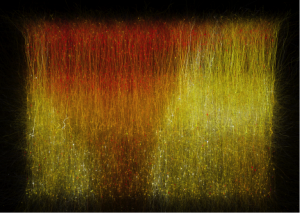
Imagen extraida de Blue Brain project [1]
Este grupo de trabajo ha realizado numerosos estudios en la búsqueda de comprender correctamente los patrones de activación neuronal, tanto a nivel local como global y lanza una propuesta matemática basada en Topología Algebraica de cómo el cerebro procesa y transfiere información
¿Por qué la Topología es tan importante?
Esta propuesta de modelización matemática de la actividad de una red neuronal animal trabaja sin parámetros (por ejemplo, no existe medida de distancia entre las neuronas del modelo) y reconstruye la información localmente a base de grafos dirigidos completos y globalmente a partir de estructuras matemáticas, llamadas complejos celulares cuyas células o símplices son los grafos anteriores. La información topológica de estos complejos se extrae en términos de números de Betti, los cuales cuentan los agujeros homológicos (en el artículo se nombran como cavidades) usando Z/2Z (notación aditiva) como cuerpo base. El seguimiento (nacimiento y muerte) de estos agujeros en el transcurso temporal de un video de activación neuronal es el útil matemático básico de estos investigadores a la hora de desemarañar cómo funciona un cerebro animal ante un estímulo. Esta técnica de topología computacional se llama persistencia homológica [2].
Grafos completos dirigidos en la reconstrucción y seguimiento temporal de agujeros homológicos en el análisis
El estudio usa un modelo de cerebro de rata construido digitalmente, que reproduce la actividad neuronal a partir de experimentos en los que las ratas son expuestas a estímulos. La actividad neuronal se extrae y analiza de los videos anteriormente descritos. Las redes neuronales han sido previamente estudiadas usando grafos estructurales no-dirigidos. En este reciente estudio [2], se estudia subgrafos dirigidos del estructural llamados funcionales. Estos últimos contienen sólo las conexiones que se activan en un periodo de tiempo concreto. Podrían describirse informalmente como conjuntos de conexiones sinápticas que ocurren en una “escena” concreta del video de análisis. Existe, por tanto, un grafo dirigido global para cada escena y se trata de saber como estos grafos que determinan el flujo de información cambian en el transcurso del video. Un grafo dirigido completo (directed clique, en inglés) es aquel en que todo vértice (neurona) está conectado a otro vértice por medio de una arista (necesariamente dirigida). Existe una neurona fuente de la cual todos las aristas dirigidas salen y una neurona sumidero al cual todos los lados dirigidos llegan. A partir del grafo dirigido global y para cada instante de tiempo, los subgrafos dirigidos completos de n neuronas determinan símplices o bloques (n-1)-dimensionales de un objeto subdividido coherentemente en símplices, que llamaremos complejo simplicial a partir de ahora.
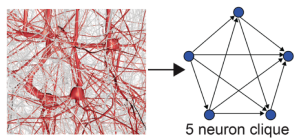
Imagen extraida de [2], Figure 1B3. Esta imagen muestra un zoom de un 5-clique neuronal, junto su correspondiente símplice a la derecha
Los investigadores encontraron que en ciertos lapsos de tiempo en el video de análisis, un gran número de símplices de dimensión cada vez mayor “nacían” al tiempo que la información fluía abundantemente entre las neuronas. Tras esta explosión de comunicación sináptica, de pronto todos los grafos dirigidos completos se desvanecían, indicando que el cerebro había finalizado de procesar la información nueva. Este comportamiento genera de forma natural la hipótesis de trabajo plausible que la actividad neuronal en un instante de tiempo está ligada a su complejo simplicial subyacente, que posee aproximadamente diez mil símplices de dimension cero (neuronas), siendo frecuentemente 7 la mayor dimension de los simplices detectados (aunque los investigadores confirman que han detectado en ocasiones hasta símplices de dimensión 11).
El análisis computacional de la información homológica de estos complejos simpliciales {Ct} para cada instante de tiempo del video permitió a los investigadores no sólo contar el número de agujeros en cada dimensión del complejo Ct (concretamente, calculando sus números de Betti) sino también “seguir su rastro” en los complejos temporales siguientes, certificando así el nacimiento y muerte de cada agujero del video por medio de intervalos de tiempo.
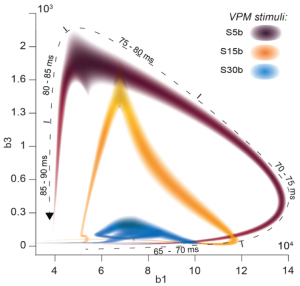
Imagen extraída de [2] Figure 6B
El grafo de la figura muestra la formación de agujeros homológicos en el tiempo. El eje horizontal corresponde al primer número de Betti y el eje vertical al tercer número de Betti.
La espiral se dibuja con respecto al tiempo, tal y como se indica sobre la curva en el texto que expresa milisegundos. Se observa que al principio, existe un fuerte crecimiento en el tercer número de Betti, seguido de un fuerte crecimiento del primero, decreciendo el tercero y, finalmente, un rápido descenso en el primero hasta una desaparición completa de los agujeros.
Desde la perspectiva del video de activación neuronal, los investigadores interpretan esto como una aparición inicial de muchos símplices 1-dimensionales, creando agujeros de la misma dimensión. El número de símplices 2 y 3 dimensionales crece en el tiempo, aportando conexiones extra entre los símplices 1-dimensionales, de tal forma que los agujeros de menor dimensión se reemplazan por otros de mayor dimensión. Cuando el número de agujeros de dimensiones más alta es máxima es cuando el cerebro parece haber terminado de procesar la información.
«La aparición de cavidades de alta dimensionalidad cuando el cerebro procesa información significa que las neuronas de la red reaccionan a los estímulos de una manera extremadamente organizada», dice Levi, uno de los investigadores del proyecto. “Es como si el cerebro reaccionara a un estímulo construyendo y luego arrasando una torre de bloques multidimensionales, comenzando con aristas (1D), luego cuadrados (2D), luego cubos (3D), y luego geometrías más complejas con 4D, 5D, etcétera. La progresión de la actividad a través del cerebro se asemeja a un castillo de arena multidimensional que se materializa fuera de la arena y luego se desintegra», describe.
La gran pregunta que estos investigadores se están haciendo ahora es si la complejidad de las tareas que podemos realizar depende de la complejidad de los ‘castillos de arena’ multidimensionales que el cerebro puede construir. La neurociencia también ha estado luchando por encontrar dónde almacena el cerebro sus recuerdos. «Pueden estar ‘escondidos’ en cavidades de gran dimensión», especula Markram, director del proyecto Blue Brain.
Discusión del modelo desde la perspectiva topológica
Es claro que la formación dependiente del tiempo de símplices o grafos completos dirigidos mide en el modelo descrito el flujo local de información, mientras el flujo global lo hace en términos de generación y muerte de agujeros .
Desde la perspectiva física del dato (“hilos” geométricos conectando neuronas que se activan en el mallado neuronal estructural del cerebro ante un estímulo), el hecho de construir el modelo en 7D+t (o 11D+t) en vez de en 3D+t (por ejemplo, tratando imágenes de resonancia magnética funcional –fMRI- del cerebro), aparece artificiosa. No obstante, la información homológica en el video 3D+t se limitaría a agujeros 1-dimensionales en el mallado estructural y no podría capturar topológicamente hablando a las configuraciones de dos o más agujeros 1-dimensionales con una sola fuente y sumidero. La reconstrucción del complejo simplicial de grafos completos dirigidos permite ver estas configuraciones, bien como símplices del complejo, bien como agujeros del mismo, permitiendo una clasificación completa de las configuraciones en este sentido.
En lo concerniente al análisis topológico, la técnica de persistencia homológica empleada en el artículo no tiene en cuenta la relación de los agujeros homológicos entre sí en un complejo temporal Ct. Agujeros n-dimensionales maximales en Ct pueden estar fuertemente homológicamente relacionado con agujeros de menor dimension (como por ejemplo que un agujero cuatro dimensional se encuentre “delineado” dentro de una componente conexa –agujero 0-dimensional- concreta del complejo). Estos podrían generar conjuntamente patrones de reconocimiento de agujeros maximales que ayudarían grandemente a la elucidación del comportamiento topológico de la activación neuronal basado en este modelo. Otra posibilidad de intentar mejorar el análisis sería el uso de una estadística de agujeros homológicos de segundo, tercer o de orden más elevado, adaptando al contexto topológico la clásica teoría estadística de matrices de coocurrencia. La idea sería de establecer matrices donde por filas y columnas aparecieran ciclos generadores de agujeros de dimensiones diferentes y el valor de la posición (i,j) sería 1 si el agujero etiquetado como i estuviera fuertemente homológicamente relacionado con el agujero j (en el sentido de que haya una operación (co)homológica derivada de la relación «ser borde de», que envie el primero en el segundo).
PARA SABER MAS:
[1] The Blue Brain Project – A Swiss Brain Initiative. https://bluebrain.epfl.ch/
[2] M. Reimann, M. Nolte, M. Scolamiero, K. Turner, R. Perin, G. Chindemi, P. Dłotko, R. Levi, K. Hess, H.Markram. Cliques of Neurons Bound into Cavities Provide a Missing Link between Structure and Function. Front. Comput. Neurosci 12 June 2017, doi.org/10.3389/fncom.2017.00048
[3] Edelsbrunner, H., & Harer, J. (2008). Persistent homology-a survey. Contemporary mathematics, 453, 257-282.

Dejar una contestacion