Un ejemplo sencillo de modelización matemática: El crecimiento de poblaciones.

En una entrada anterior discutimos la importancia del método científico descrito por Galileo en su libro Il Saggiatore. Allí vimos que para “entender” el mundo que nos rodea necesitamos usar la combinación de la experiencia (realización de experimentos) con las matemáticas (modelos matemáticos). De esta segunda parte es de la que vamos a tratar en este entrada: de la modelización matemática. Recordemos que la primera fase del método científico consiste en formular, a partir de las observaciones de cierto fenómeno, las ecuaciones matemáticas para describirlas. Dichas ecuaciones, en una segunda fase, nos deberían permitir predecir los resultados de futuras observaciones pues en caso contrario habría que desecharlas o modificarlas por otras que sí lo hagan. ¿Cómo encontrar dichas ecuaciones? Es justo de eso de lo que se ocupa la modelización matemática: en dar con las ecuaciones correctas para describir los correspondientes fenómenos. Groso modo la modelización consta de los siguientes pasos:

1. Cuantificar el fenómeno, o sea, convertir de alguna forma en cantidades (números) las observaciones que hacemos. Esto puede ser muy “sencillo” (por ejemplo si estamos interesados en medir velocidades podemos medir las distancias y los tiempos) pero puede ser muy «complicado» (por ejemplo medir la magnitud de una erupción de un volcán, algo de lo que hablaremos en una entrada futura).

2. Postular las ecuaciones que relacionan las magnitudes, en otras palabras, encontrar el conjunto de fórmulas matemáticas que las relacionan. Aquí juega un papel fundamental tanto la intuición del científico como la suerte (un ejemplo que merece una entrada aparte es de cómo Schrödinger descubrió la ecuación que hoy día lleva su nombre).

3. Comparar los resultados obtenidos a partir de las ecuaciones matemáticas del paso dos con las observaciones hechas en el paso uno y realizar otras observaciones que puedan confirmar el modelo. En caso de que no lo confirmen intentar modificarlo convenientemente y repetir la comparación.

Por simplicidad vamos a mostrar como funciona la modelización con un ejemplo muy sencillo de entender: el crecimiento de una población. Imaginemos que queremos saber como crece una población. Uno de los modelos más simples corresponde al  modelo de Malthus  discutido ya en este blog y que fue propuesto por el inglés Thomas Maltus en 1798 en su famoso ensayo “Essay on the Principle of Population” (para más detalle vea el lector dicha entrada). En él Malthus, basándose en datos de la población de los Estados Unidos en el siglo XVIII, postula que el crecimiento de la población humana es exponencial. Matemáticamente lo que esto quiere decir es que la velocidad de crecimiento de la población es proporcional a la misma, es decir, \(p’(t) = r p(t)\), donde \(p(t)\) es el número de individuos de la población en el momento de tiempo \(t\) y \(r\) es cierta constante (conocida como tasa de crecimiento de la población) que debemos deducir de los datos experimentales y \(p’(t)\) es la derivada de \(p(t)\) (que es justamente nos da la velocidad de crecimiento). La solución de la ecuación anterior (que es una ecuación diferencial) es \(p(t)=p_0 e^{r(t-t_0)}\) donde \(p_0\) es el número de individuos en el momento inicial \(t=t_0\). Está claro es que si \(r<0\) la especie estará condenada a la extinción (ver figura de la izquierda) mientras que si \(r>0\) tendremos un crecimiento exponencial (ver figura de la derecha) lo cual, tal y como se comenta en dicha entrada, no es realista.

Y no es realista entre otras cosas porque si aumenta mucho el número de individuos de la población estos estarán obligados a luchar por el espacio y los recursos ya que ambos son finitos. Malthus estimaba que la producción de alimentos crecía en progresión aritmética (es decir, proporcional al número de individuos) mientras que la población humanos crecía de forma exponencial por lo que concluyó que el ser humano estaba predestinado a subsistir en el hambre y la pobreza. Aunque el análisis de Malthus resultó incorrecto tuvo una tremenda influencia en su época. De hecho fue la lectura del ensayo de Malthus en octubre 1838 durante su viaje alrededor del mundo lo que indujo a Darwin el mecanismo de selección natural universalmente aceptado hoy día.

¿Cómo podemos corregir el modelo malthusiano de forma que sus previsiones sean más acordes con la experiencia? En primer lugar hay que tener en cuenta que a corto plazo y en unas condiciones óptimas de espacio y recursos (como las de Norteamérica en el siglo XVIII) el modelo de Malthus funciona bastante bien y solo cuando el número de individuos es muy grande es que empieza a fallar. Por otro lado es bien conocido que si el número de individuos crece este tiende estabilizarse en torno a cierto valor crítico. Así pues, el nuevo modelo tiene que, de alguna forma, predecir para poblaciones pequeñas un crecimiento exponencial y cuando la población sea muy numerosa, una estabilización de la misma. La solución al problema vino de la mano del matemático y biólogo belga P. F. Verhulst quien en 1837 propuso el modelo conocido como modelo logístico. Su idea consistió en sustraerle al término \(r p\) de la ecuación de Malthus el término \(cp^2\). Así la nueva ecuación sería

\(p'(t)=r\,p(t)-c p^2(t),\qquad p(t_0)=p_0,\quad r,c>0. \)

En general \(c\) ha de ser mucho más pequeño que \(r\) de forma que si \(p\) no es muy grande la ecuación de Malthus es una aproximación bastante buena, pero si \(p\) comienza a crecer demasiado entonces el término \(-c p^2\) se hace mayor y termina frenando el crecimiento exponencial. Usualmente \(c\) se escribe como el cociente \(r/K\) donde \(K\) se conoce como la capacidad de carga del medio y es una constante que está ligada a los recursos del hábitat. La solución de la ecuación de Verhulst es

\(p(t)=\displaystyle \frac{r\, p_0}{c\,p_0 +(r-c\,p_0)e^{-r\,(t-t_0)}}, \)

a partir de la cual se puede comprobar que para tiempos cercanos al tiempo inicial \(t_0\) y para valores pequeños de \(p_0\), \(p(t) \approx p_0 e^{r(t-t_0)}\), es decir, se recupera la solución exponencial de Malthus. Por otro lado, si \(t\) es muy grande (mucho más que \(t_0\)), entonces \(p(t)\approx r/c=K\), es decir la población se estabiliza. El comportamiento de la población según el modelo logístico lo podemos ver en la siguiente figura:

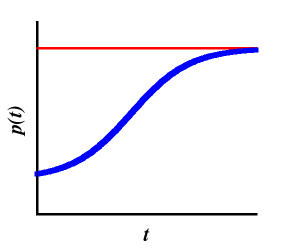
Usemos ahora los datos recopilados por la Oficina del Censo de los Estados Unidos de la población mundial para estimar los parámetros de la ecuación de Verhulst y deducir que podría pasar con la misma en un futuro no muy lejano. Si usamos los datos recopilados a partir de 1950 (en ese año se estimaba que el número de personas era de \(2.558\cdot 10^9\)) hasta 2014 se obtiene para \(r\) el valor \(r=0.01731313844533347\). Así, comparando el valor que nos da la fórmula de Malthus \(p(2000)\approx 6.078375327752732\cdot 10^9\) vemos que es bastante parecido al valor real estimado de \(6.088571383 \cdot 10^9\) personas. En cambio la predicción para el año 2010 da \(p(2010)= 7.22732389676767\cdot 10^9\) que empieza a alejarse a la estimada por el censo que es de \(6.866332358 \cdot 10^9\). Si usamos ahora el modelo logístico manteniendo para \(r\) el mismo valor de antes y tomando para \(c\) el valor \(8.361178966147587\cdot 10^{-14}\) (que se obtiene a a partir de los datos del censo) podemos usar la función de Verhulst para estimar los valores de la población mundial. Así, en el 2010 el modelo logístico predice una población de \(7.067929710275726 \cdot 10^9\), que es algo mejor (pero no mucho) que el predicho por el modelo maltusiano (véase la figura).

Lo interesante es comprobar que a medida que nos alejamos en el tiempo, el modelo logístico predice la estabilización de la población en un valor cercano a \(2\cdot 10^{11}\), cantidad que se alcanzaría en el año 2200 aproximadamente. El resultado lo vemos en la siguiente gráfica.

Para concluir debemos decir que el modelo logístico sigue siendo muy simple pues no tiene en cuenta ni epidemias, ni guerras, ni terremotos y otros desastres que desgraciadamente siguen ocurriendo en el mundo en que vivimos. Si queremos tener en cuenta dichas situaciones hay que incluir nuevos términos en la ecuación, términos que en general no son fáciles de intuir. Seguramente, amigo lector, buscando podrá encontrar varios modelos que intentan tenerlos en cuenta y si no siempre puede intentarlo por su cuenta.