Divertimento:
Un cocinero se dispone a ejecutar a un pavo para la cena de navidad, pero el animal se revuelve y escapa. El cocinero, sorprendido, tarda unos segundos en reaccionar. Cuando lo hace el pavo está ya en un punto \(P_0\) situado a 10 metros del punto \(Q_0\) donde se encuentra el cocinero. El pavo comienza a correr en dirección perpendicular a \(P_0 Q_0\) y mantiene su trayectoria y velocidad constantes. En el mismo instante, el cocinero comienza perseguir al pavo corriendo a la misma velocidad que éste, y apuntando siempre en su dirección. El cocinero nunca alcanzará al pavo, pero tiene un lazo de 5 metros de longitud con el cual pretende atraparlo. ¿Lo consigue en algún momento?
Solución:
Sea \(v\) la velocidad del cocinero y del pavo, y \(\alpha\) el ángulo que forman las direcciones de sus trayectorias. Denotemos por \(P\) y \(Q\) las posiciones del pavo y del cocinero, y por \(S\) a la proyección de la posición del cocinero sobre la recta \(P_0 P\).
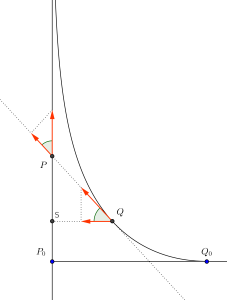
La distancia entre el pavo y el cocinero se mide sobre la recta \(PQ\). En esta dirección, el cocinero corre con velocidad \(v\), y el pavo con velocidad \(v \cos \alpha\). Por tanto, la distancia \(PQ\) disminuye con una velocidad \(v-v\cos\alpha\). Análogamente, la distancia \(PS\) aumenta con una velocidad \(v-v \cos \alpha\). Se deduce entonces que la suma \(PS+PQ\) permanece constante. Como \(P_0Q_0=10\) y \(P_0S_0=0\), tenemos que $$PS+PQ=10.$$
Por otra parte, como \(PQ>PS\),
$$
10=PS+PQ < 2PQ,
$$
de donde \(PQ>5\), y el cocinero nunca atrapará al pavo con un lazo de 5 metros.
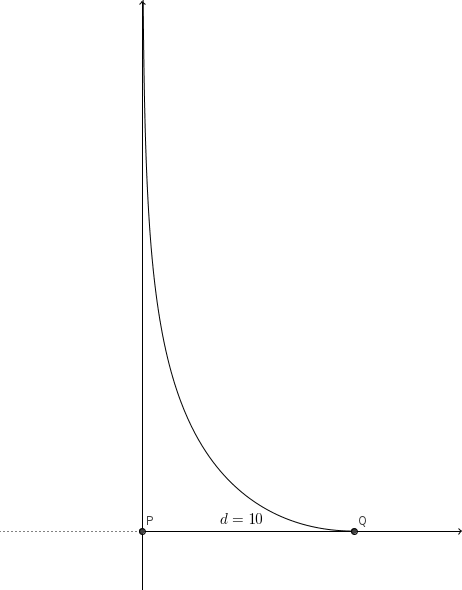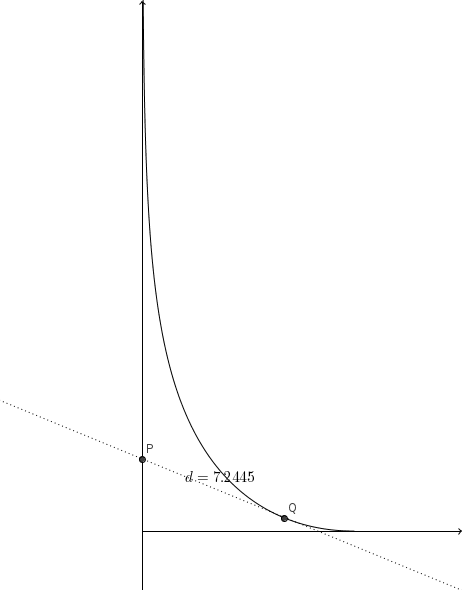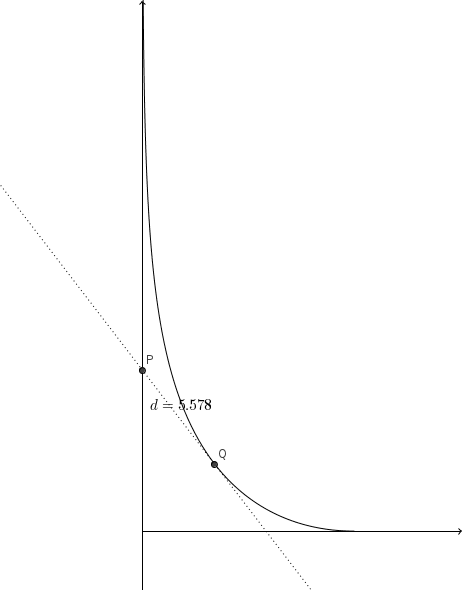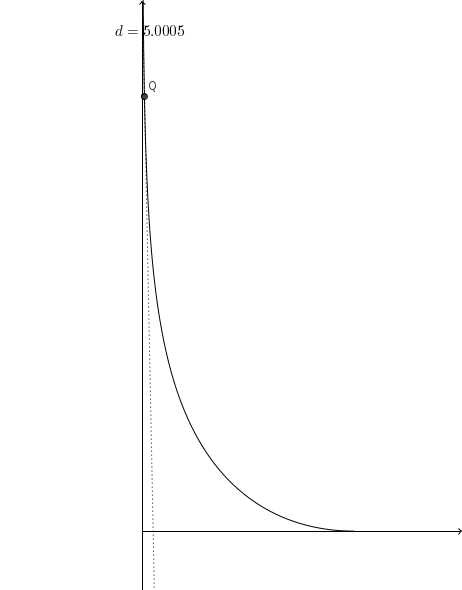

Dejar una contestacion