Publicamos la solución al divertimento Pentágono. Gracias a Alberto Castaño y a Cristóbal Sánchez-Rubio por las soluciones que han aportado.
Divertimento:
Un pentágono regular ABCDE (nombrados los vértices en el sentido de las agujas del reloj) de lado 1 dm tiene el lado AB apoyado en una recta horizontal. El pentágono gira sobre el vértice A hasta que el lado EA queda apoyado. El proceso continúa, girando sucesivamente sobre los vértices E, D y C, de modo que al final es el lado BC el que está sobre la recta. Se pide obtener la longitud del arco descrito por el punto B. (En un primer nivel, se pide obtener el resultado con dos decimales exactos. En un segundo nivel, se pide el valor exacto).
Solución:
Solución enviada por Cristóbal Sánchez-Rubio.
Como el problema tiene una clara simetría, basta medir dos arcos de amplitud 72º y radios 1 y \(\Phi=\frac{1+\sqrt{5}}{2}\) (número áureo) que es la razón entre la diagonal y el lado de un pentágono regular. El resto es puro cálculo.
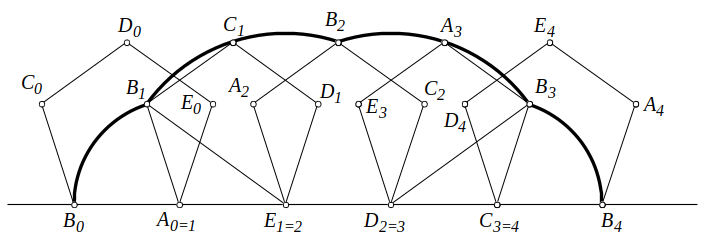
$$ 2 \frac{2\pi + 2 \pi \Phi}{5}=\frac{ 4\pi}{5}(1+\Phi) =\frac{ 4\pi}{5}\frac{3+\sqrt{5}}{2}=\frac{2\pi}{5}(3+\sqrt{5})=6.5798\ldots$$

Dejar una contestacion