Solución: herederos

Divertimento:

Los dos herederos de una finca rectangular que tiene dos casas situadas cerca de dos vértices opuestos sobre uno de los lados mayores, acuerdan dividirla en dos fincas de igual superficie uniendo los puntos medios de los dichos lados mayores, que es la linde de menor longitud. La presencia de las casas hace difícil hallar el punto medio de ese lado. Suponiendo que se puede ir en línea recta entre dos puntos cualesquiera dejando el rastro en el suelo, indique cómo podría dividirse la finca.

Encuentra el punto medio de un segmento AB utilizando exclusivamente una regla sin graduar teniendo la ayuda de una recta paralela a la recta AB.

Solución:

Se traza por A una recta que corta a la paralela en M y por B otra que corta a la paralela en N. Ambas rectas se cortan en V. Luego se unen A con N y B con M. Estas dos rectas se cortan en Q. La recta VQ se corta con AB en C.

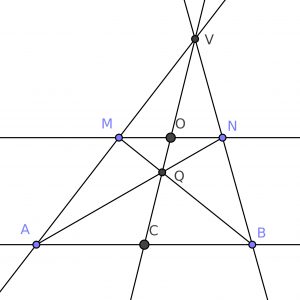
Los triángulos VON y VCB son semejantes, y también lo son los triángulos VOM y VCA. Por tanto $$ \frac{VO}{VC} = \frac{ON}{CB}, \qquad \frac{VO}{VC} = \frac{OM}{CA},$$ de donde $$\frac{ON}{CB} = \frac{OM}{CA}.$$ Análogamente, los triángulos QON y QCA son semejantes, y también lo son los triángulos QOM y QCB, y se deduce que $$\frac{ON}{CA} = \frac{OM}{CB}.$$ Por tanto, existen dos números reales positivos $\alpha, \beta$ tales que $$ON= \alpha CB, \qquad OM=\alpha CA, \qquad ON = \beta CA, \qquad OM=\beta CB,$$ de donde $$1= \frac{\alpha}{\beta}\frac{CB}{CA}, \qquad 1 = \frac{\alpha}{\beta} \frac{CA}{CB}.$$ Se deduce que $1=\alpha^2 / \beta^2$, de donde $\alpha=\beta$. Así, $$MN=OM+ON=2 \alpha CA, \qquad MN=OM+ON=2 \alpha CB,$$ de donde $CA = CB$, y C es el punto medio pedido.