Producto de Euler y Ceros

La función zeta y sus propiedades.

Hablamos este mes de la Hipótesis de Riemann. La historia que contaremos tiene dos ideas fundamentales y las dos tienen su origen en Euler. Pueden verse en el gran libro de Euler Introductio in Analysin Infinitorum.

La primera idea se resume en el producto de Euler $$\prod_{p}\Bigl(1-\frac{1}{p^s}\Bigr)^{-1}=\sum_{n=1}^\infty \frac{1}{n^s},\qquad \textrm{Re}(s)>1.$$La segunda aparece en su trabajo sobre las particiones. Para lo que Euler considera, de manera incipiente, las primeras formas modulares.

El producto de Euler solo converge para \(\textrm{Re}(s)>1\), pero define en esa región una función analítica que se extiende de manera única a todo el plano. Aparte de un polo en \(s=1\), se anula en los números pares negativos, los llamados ceros triviales y tiene además infinitos ceros mucho mas interesantes situados en la banda \(0<\textrm{Re}<1\). La distribución de los números primos depende fuertemente de estos ceros.

La función \(\zeta(s)\) verifica además la ecuación funcional: \(\Lambda(s)=\Lambda(1-s)\) donde $$\Lambda(s)=\pi^{-s/2}\Gamma(s/2)\zeta(s).$$

Riemann que conocía el producto de Euler y la Ecuación Funcional conjeturó que los ceros no triviales de \(\zeta(s)\) debían estar todos en la recta \(\textrm{Re}(s)=\frac12\). Pero hasta ahora esta afirmación no ha sido probada ni refutada. Se sabe que casi el 50% de los ceros no triviales están en la recta crítica y que los primeros ceros están todos en la recta (quizás los \(10^{13}\) primeros ceros, aunque esta cifra no ha sido confirmada). 

La función zeta es la mas simple de un conjunto de funciones, las funciones \(L\), que aparecen en numerosos problemas de Teoría de Números. 

Otras funciones \(L\) y formas modulares.

Podríamos decir que una función \(L\) es una función que admite un desarrollo en serie de Dirichlet \(\sum_n a_n n^{-s}\), un producto de Euler y una ecuación funcional. Los primeros ejemplos los construyó Dirichlet para probar con ellos el teorema de que toda progresión aritmética $$a,\ a+b,\ a+2b,\ a+3b,\ \dots$$ contiene infinitos primos si \(a\) y \(b\) son primos entre sí. Mas tarde Dedekind definió la función zeta de un cuerpo de números algebraicos, que también es una función \(L\). 

Las formas modulares son funciones analíticas definidas en el semiplano superior y que tienen propiedades de simetría muy notables. Como hemos dicho ya Euler consideró alguna, pero realmente aparecen con la teoría de las funciones elípticas en el siglo XIX. Tienen un desarrollo del tipo \(f(z)=\sum_{n=0}^\infty a_nq^{n/h}\) siendo \(q=e^{2\pi iz}\). 

Un ejemplo de como están relacionados los dos conceptos lo dio Ramanujan que consideró la forma modular $$q\prod_{n=1}^\infty(1-q^n)^{24}=\sum_{n=1}^\infty \tau(n) q^n.$$ Estudió las propiedades aritméticas de los coeficientes \(\tau(n)\) y escribió el producto de Euler para la correspondiente serie de Dirichlet $$\sum_{n=1}^\infty\frac{\tau(n)}{n^s}=\prod_p\Bigl(1-\frac{\tau(p)}{p^s}+\frac{p^{11}}{p^{2s}}\Bigr)^{-1}.$$ Mordell probó esto y además la ecuación funcional \(\Lambda(s)=\Lambda(12-s)\) para $$\Lambda(s)=(2\pi)^{-s}\Gamma(s)\sum_{n=1}^\infty\frac{\tau(n)}{n^s}.$$ Hay una hipótesis de Riemann relativa a esta función, los ceros no triviales estarán situados en la recta crítica: en este caso \(\textrm{Re}(s)=6\). (Con una adecuada renormalización podemos situar la recta crítica en \(\textrm{Re}(s)=\frac12\) y la banda crítica en \(0<\textrm{Re}(s)<1\).)

No toda forma modular conduce a una función \(L\). No todas tienen un producto de Euler. Hecke demostró que esto ocurre si y sólo si la forma modular es autofunción de los operadores de Hecke. Hay otra fuente más de funciones \(L\) que vienen de formas automorfas (una generalización de las formas modulares) pero no entraremos en eso. También hay una definición axiomática: la clase de Selberg. De todas ellas se conjetura la correspondiente hipótesis de Riemann. El conjunto de estas hipótesis es la GRH (hipótesis generalizada de Riemann). 

El trabajo de Andrew R. Booker y Frank Thorne.

Sea \(L(s)\) una verdadera función \(L\), esto es, una serie de Dirichlet que admite un producto de Euler y una ecuación funcional. Entonces tenemos una banda crítica \(0<\textrm{Re}(s)<1\), el producto de Euler prueba que no hay ceros cuando \(\textrm{Re}(s)\ge1\). Pero además se conjetura que los ceros (no triviales) están situados en la recta crítica. Cuando no hay producto de Euler los ceros no se están en la recta. 

Andrew R. Booker y Frank Thorne se preguntan sobre la importancia del producto de Euler. Todo el mundo piensa que la ecuación funcional hace que los ceros se sitúen con preferencia en la recta crítica, quizás el producto de Euler prohibe ceros a la derecha de \(\sigma>1\) y entonces la ecuación funcional los lleva a la recta crítica. Y se preguntan, podría haber una serie de Dirichlet con ecuación funcional, que no tenga ceros en \(\sigma>1\) a pesar de no tener producto de Euler. 

Para ello consideran series de Dirichlet con ecuación funcional, lo mas fácil es admitir que viene de una forma modular o bien de una forma automorfa. La sorprendente conclusión del trabajo de Booker y Thorne es que si una tal serie de Dirichlet no tiene ceros en \(\sigma>1\), entonces tiene un producto de Euler. 

Para una función razonable (que venga de una forma modular o automorfa) o hay ceros en \(\sigma>1\) o hay producto de Euler. 

La importancia del resultado es que refuerza la idea de que el producto de Euler ha de jugar un papel en la prueba de la hipótesis de Riemann. 

En realidad Booker y Thorne extienden un resultado anterior de Eric Saias y Andreas Weingartner que probaron lo mismo para series de Dirichlet \(f(s)=\sum_{n=1}^\infty a_n n^{-s}\) con coeficientes periódicos, esto es que para un \(N\) fijo satisfacen \(a_{n+N}=a_n\). O bien existe \(a\) con \(\textrm{Re}(a)>1\) tal que \(f(a)=0\) o bien \(f(s)=P(s)L(s)\), donde \(L(s)\) admite un producto de Euler, es decir, en ese caso \(L(s)\) es una de las funciones consideradas por Dirichlet, y \(P(s)\) es un polinomio de Dirichlet \(P(s)=\sum_{n=1}^K b_n n^{-s}\), una suma finita que además no se anula en \(\textrm{Re}(s)>1\).

¿Porqué es tan difícil probar la hipótesis de Riemann?

Naturalmente una pregunta como esta no tiene una respuesta fácil. Pero hay varias razones que pueden darse. 

(a) La función \(\zeta(s)\) tiene un comportamiento caótico.

Conocemos muchas funciones cuyos ceros están situados en una recta. El seno y el coseno son los ejemplos mas simples. Las funciones de Bessel serían los siguientes que vienen a la mente, o la inversa de la función Gamma. En todos estos casos la función es extremadamente simple. Los gráficos de estas funciones son muy regulares, no hay sorpresas en ellos. Como consecuencia los ceros son predecibles. 

La función zeta no sigue un patrón. Para verlo lo mejor es tener en cuenta que la ecuación funcional implica que la función en la recta crítica es salvo por factores simples una función real de variable real. En el caso de la función zeta es la función \(Z(t)\) de Riemann-Siegel (a veces llamada función de Hardy).

En la figura vemos representada esta función en en rango \((0,100)\), pero por comparación hemos añadido una figura en el rango \((a-5,a+5)\) siendo \(a=388\,858\,885.691009\).

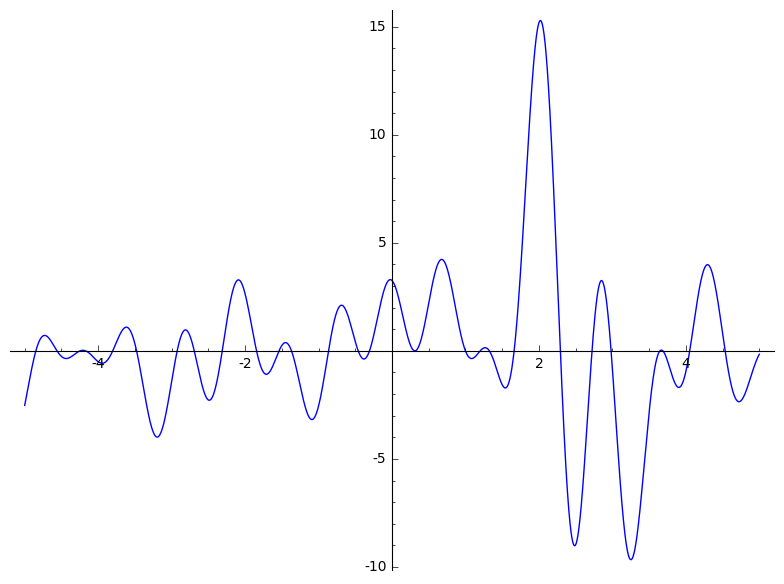
Una forma de probar la existencia de ceros es dar formulas asintóticas, estas son aproximaciones que permiten probar que la función cambia de signo y por tanto la existencia de ceros. Pero con una función como la zeta de Riemann ninguna aproximación parece suficiente. En la figura vemos que en el punto \(a+0.3\) aproximadamente la función cambia de signo, pero apenas una mijita. 

(b) Funciones semejantes que satisfacen la hipótesis de Riemann ya no son caóticas. 

Riemann consiguió escribir una transformada de Fourier $$\xi(t)=2\int_0^\infty \Phi(u)\cos(tu)\,du$$ que tiene justo los ceros de \(Z(t)\). Pólya tuvo la idea de tomar una función \(\Phi^*(u)\) que se diferencia extremadamente poco de la verdadera \(\Phi(u)\) y consiguió probar que la correspondiente \(\xi^*(t)\) tiene todos sus ceros reales. Pero, un análisis de la función \(\xi^*(t)\) nos hace ver que precisamente esta función es muy regular sus ceros han perdido esa distribución anómala de la \(Z(t)\). 

(c) La función de Titchmarsh.

En el libro de Titchmarsh sobre la función zeta se construye una serie de Dirichlet \(T(s)=\sum_{n=1}^\infty a_n n^{-s}\) que es combinación lineal de 4 funciones \(L\) de Dirichlet, que verifica la ecuación funcional $$\Lambda(s)=\Lambda(1-s), \qquad \text{donde}\quad \Lambda(s)=(5/\pi)^{s/2}\Gamma((1+s)/2)T(s)$$ Sin embargo \(T(s)\) no tiene un producto de Euler. Tampoco verifica la hipótesis de Riemann. En el gráfico vemos que entre 80 y 90 hay un máximo negativo que en estas funciones significa que en ese lugar hay dos ceros complejos, fuera de la recta crítica. 

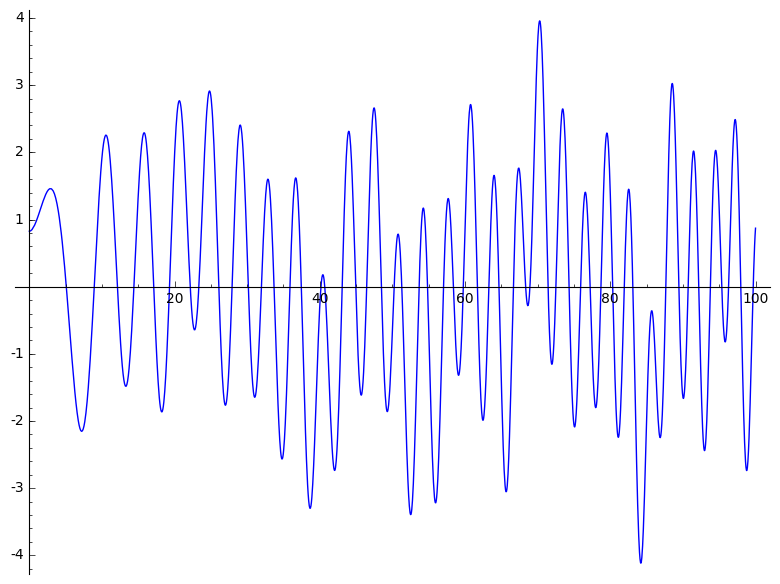
La función de Titchmarsh esta dada por una serie de Dirichlet, verifica una ecuación funcional y no tiene un producto de Euler. No satisface la hipótesis de Riemann. Es difícil imaginar una prueba de la la HR para \(\zeta(s)\), que a la vez no «demuestre» que \(T(s)\) satisface la HR, que sabemos que no es cierto.

Peter Sarnak una de las autoridades en el tema y editor de la revista Annals of Mathematics afirma en la conferencia que citamos en las referencias, que el ‘Annals’ recibe cada semana alrededor de tres pruebas de la Hipótesis de Riemann. El 99% de las mismas pueden rechazarse inmediatamente por que no usan mas que la ecuación funcional. La prueba no puede ser correcta pues igualmente se aplicaría a la función \(T(s)\) definida en Titchmarsh. 

Pero el problema es que el producto es convergente solo fuera de la banda crítica. Nadie ha conseguido usarlo con provecho en el entorno de la recta crítica.

(d) Resultados de Tao sobre la constante de Bruijn-Newmann.

Muchos intentos de atacar la hipótesis de Riemann vienen de deformar la función y tratar de ver el comportamiento de los ceros. Esto es el camino de de Bruijn quién define la función, partiendo de nuevo de la representación de Riemann $$H_t(z)=\frac12\int_{-\infty}^{+\infty} e^{tu^2}\Phi(u) e^{izu}\,du.$$ la HR equivale a que \(H_0(z)\) tiene sus ceros reales. \(H_t(z)\) es la evolución de \(H_0(z)\) mediante la ecuación del calor (pero con el tiempo invertido), es decir cuando \(t\) crece es como se enfrían los ceros. (Ver la entrada anterior: Si la hipótesis de Riemann es cierta, será por los pelos.)

Los resultados recientes de Rodgers y Tao sobre la constante de Bruijn-Newmann demuestran que la más ligera deformación \(H_{-\varepsilon}(z)\) hacía valores negativos de \(t\) hacen aparecer raíces fuera de la recta. Esto implica también que existen funciones muy similares a la función zeta de Riemann que no satisfacen la hipótesis de Riemann. 

(e) Muchos lo han intentado sin éxito.

Esto nos dice que el problema no es trivial. Desde que Riemann formuló la hipótesis muchos de los mejores matemáticos han tratado de atacarla. Todos los intentos han fracasado. Una buena recomendación a quién crea tener una prueba de la hipótesis de Riemann es que explique porqué su prueba se aplica a \(\zeta(s)\) y no a la función de Titchmarsh. 

Para saber mas.

Sorprendentemente (o no!) la primera edición del libro de Euler en castellano es del año 2001:

L. Euler, Introducción al análisis de los infinitos, Edición de A. J. Durán y J. Pérez, Real Sociedad Matemática Española y S.A.E.M.~Thales, Sevilla, 2001.

El motivo de esta entrada es el artículo:

A. R. Booker, F. Torne, Zeros of \(L\)-functions outside the critical strip, Algebra Number Theory 8 (2014) 2027-2042.

Como hemos dicho este trabajo es una mejora de otro anterior

E. Saias, A. Weingartner, Zeros of Dirichlet series with periodic coefficients, Acta Arith. 140 (2009) 335-344,

que es mas fácil de entender. 

Algunos comentarios sobre las posibles pruebas de la hipótesis de Riemann las he sacado de la muy interesante conferencia de Peter Sarnak:

P. Sarnak, Commentary and comparisons of some approaches to GRH (2018). (YouTube). 

Las transparencias que usó Sarnak en esta conferencia son accesible en transparencias.

Una explicación excelente de los trabajos recientes de Tao sobre la constante de Bruijn-Newmann, muy accesible es la conferencia:

T. Tao Vaporizing and freezing the Riemann zeta function, Università degli Studi di Milano – Bicocca

Mucha información sobre la función \(\zeta(s)\) se encuentra en el libro clásico de Titchmarsh:

E. C. Titchmarsh, The Theory of the Riemann Zeta-function, Oxford University Press, Second ed. revised by D. R. Heath-Brown, 1986.

La función \(T(s)\) es la construida en la Sección 10.25.