Solución: Rosetón

Divertimento:

Un rosetón gótico está formado por un círculo en cuya circunferencia se colocan los vértices de un octógono regular inscrito. Con centro en cada uno de esos puntos y tomando como radio el lado del octógono, se trazan ocho arcos de circunferencia dentro del círculo que delimitan en el centro un octógono de lados curvos. ¿Qué proporción del área del círculo constituye el área del cuadrado de lados curvos ABCD?

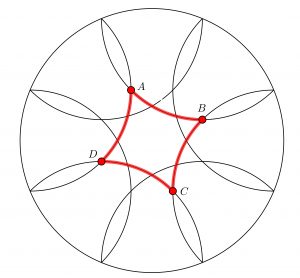
Este problema ha sido inspirado por la Colegiata de San Cosme y San Damián, en Covarrubias.

Solución:

Solución propuesta por Cristóbal Sánchez-Rubio.

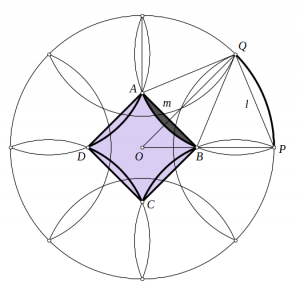
Podemos suponer sin pérdida de generalidad que el radio del círculo es 1. Llamando \(m=AB\), \(l=PQ\), el área del cuadrado curvilíneo es la de un cuadrado de lado \(m\) menos cuatro segmentos de color gris oscuro en la figura. El resto es un simple cálculo, comenzaremos por \(l\). En el triángulo isósceles \(OPQ\) con ángulo desigual de \(45º\) tenemos $$\sin \frac{45º}{2} = \frac{\sqrt{2 – \sqrt{2}}}{2} = \frac{l}{2}, \qquad l = \sqrt{2 – \sqrt{2}}.$$ Por la semejanza de los triángulos AQB y OPQ, resulta $$\frac{l}{m} = \frac{1}{l}, \qquad m = l^2 = 2 – \sqrt{2}.$$ El área del segmento gris de la figura vale $$\frac{\pi l^2}{8}- \frac{1}{2} l^2  \frac{\sqrt{2}}{2} = \frac{l^2}{4} \Big( \frac{\pi}{2} – \sqrt{2} \Big).$$ El área del cuadrado curvilíneo vale $$ m^2 – 4 \frac{l^2}{4} \Big( \frac{\pi}{2} – \sqrt{2} \Big) = l^2 \Big( l^2 – \frac{\pi}{2} + \sqrt{2} \Big) = (2- \sqrt{2})(2- \pi/2).$$ La proporción pedida es $$ \frac{1}{\pi}(2- \sqrt{2})(2- \pi/2).$$